基于加速老化试验的磁光玻璃型光学电流传感器的寿命评估
2014-09-26肖智宏于文斌张国庆郭志忠张祥龙
肖智宏,于文斌,张国庆,郭志忠,申 岩,张祥龙
(1.哈尔滨工业大学 电气工程及自动化学院,黑龙江 哈尔滨 150001;2.国网北京经济技术研究院,北京 102209)
0 引言
基于Faraday磁光效应原理的光学电流传感器OCS(Optical Current Sensor)以其无磁饱和、绝缘性能好和抗干扰能力强等优点在电力系统测量和保护中得到了广泛的关注[1-7]。阻碍OCS实用化进程的2个主要问题是测量精度的温度稳定性和长期运行可靠性。目前,OCS产品已经在智能变电站中得到了应用,而且随着技术的发展,其测量精度的温度稳定性基本能满足现场要求[8-11]。但是,其长期运行可靠性,特别是其使用寿命还无法通过现场仅有的几年运行时间获得。为了促进OCS在智能变电站中的推广应用,保证OCS的长期运行可靠性,有必要对设计的OCS的预计使用寿命进行评估。
国内外关于OCS的可靠性研究和文献还比较少。文献[12]介绍了一些有关OCS可靠性的标准和程序,但并未针对OCS的可靠性进行具体分析研究;文献[13]从OCS的光路结构的角度分析了影响其长期运行稳定性和可靠性的因素;文献[14]设计了OCS的可靠性试验内容和程序,并对其可靠性评估和寿命计算方法进行了初步探讨,但是并未给出具体定量的寿命评估方法。
本文将针对基于Faraday磁光效应原理的OCS,在分析OCS的失效模式和失效机理的基础上,提出OCS插入损耗变化量的概念,并以此作为OCS的失效判据;从模数(A/D)转换器带来的量化误差引起OCS测量误差的角度出发,对OCS的失效判据进行分析和计算;以85℃高温作为加速热应力,设计OCS的加速老化试验方案,并对样本试验数据进行分析,以获得OCS的中位寿命,并对OCS在常态温度下的预计使用寿命的置信度水平进行分析。
1 OCS的基本结构和测量原理
图1为基于Faraday磁光效应原理的OCS的基本结构示意图,它包括磁光玻璃、光纤、准直器、起偏器和检偏器等光学器件,这些构成器件都属于无源光器件,它们通过光学粘合剂粘结在一起[14]。
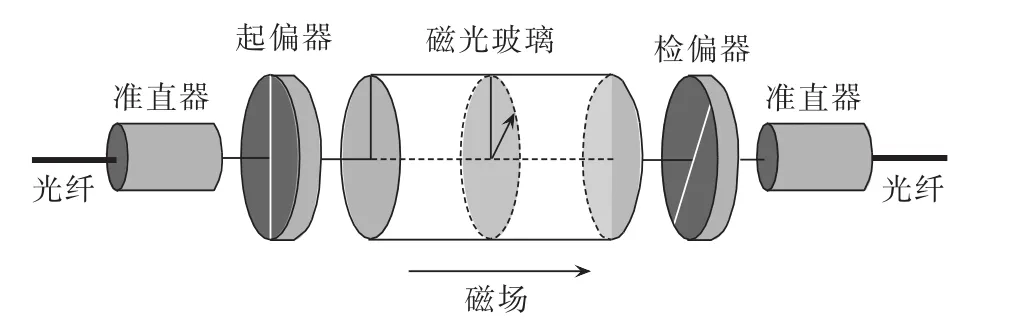
图1 OCS的结构示意图Fig.1 Structure of OCS
图2为OCS的测量系统示意图。输出光功率为P0的光源通过多模光纤射入OCS,OCS基于Faraday磁光效应原理感应被测电流i(t)后输出的光信号Px可以用下式表示:

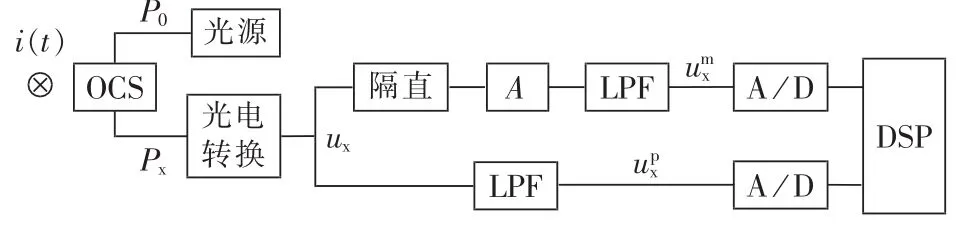
图2 OCS的测量系统示意图Fig.2 Schematic diagram of measuring system for OCS
其中,α0为光路固有损耗系数;θ为对应于被测电流 i(t)的 Faraday 旋转角。
令Ps=α0P0,称为OCS的静态工作光强,它与磁光玻璃的长度、两准直器之间的轴线倾角、起/检偏器的分光比和横向偏移以及各端面的加工精度及匹配程度等很多因素有关[13]。
根据Faraday磁光效应原理,旋转角θ可以用下式表示:

其中,V为磁光玻璃的菲尔德常数;K为与OCS结构和安装位置有关的结构参数。
一般旋转角θ比较小,有下式成立:

光信号Px输入响应度为R的光电管转换成的电信号ux可以用下式表示:
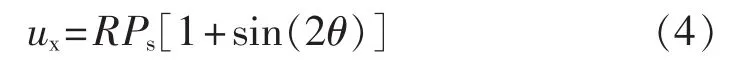
令Us=RPs,称为OCS的静态工作电压。
信号ux输入2个不同的处理通道。
a.测量通道。为了提高信号的分辨率,信号ux经过隔直放大之后经由抗混叠低通滤波器(LPF)输入A/D转换器,测量通道输出信号umx可以表示为:

其中,A为测量通道的放大倍数,其值选取与OCS的响应度和被测额定电流大小有关,但必须保证在2倍额定电流下,放大之后的信号输出幅值不超出A/D转换器的满刻度量程。
b.保护通道。信号ux经由抗混叠低通滤波器直接输入A/D转换器,保护通道输出信号upx可以表示为:

由式(2)、(3)、(5)和(6),可以得到 OCS 测得的i(t)的测量通道输出值和保护通道输出值分别为:
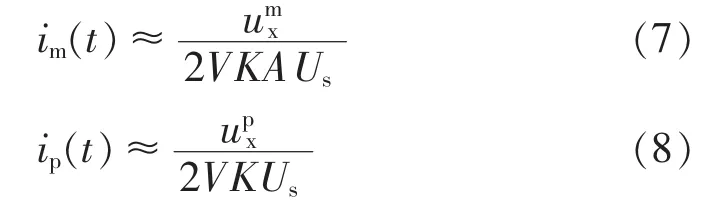
当然,在稳态时,两通道输出的结果是一致的。
2 OCS的失效模式和失效判据
2.1 失效模式和失效判据的分析
失效是指产品因为一些原因,其性能不再满足设计和应用要求。失效模式是产品失效的一种表现形式,失效机理是指引起失效的物理、化学变化等内在原因,失效影响是指每种失效对产品的使用、功能或状态所带来的后果。
影响OCS性能并阻碍其实用化进程的2个主要问题是测量精度的温度稳定性和长期运行可靠性。
a.测量精度的温度稳定性。环境温度的改变引起磁光玻璃菲尔德常数和线性双折射等的变化,从而使得OCS的测量精度存在温度漂移问题,不能满足测量要求。这一问题可以通过自愈等补偿措施得到解决[8]。
b.长期运行可靠性。这一问题集中体现在静态工作光强的稳定性方面,而静态工作光强的变化又体现在光路损耗的变化。随着运行时间的推移,其损耗变化逐步增大,最终导致OCS的失效,如分辨率的下降导致测量误差不再满足测量要求等。
OCS的结构和加工工艺水平决定了静态工作光强的稳定性,因此本文选择光路损耗的变化作为进行OCS可靠性寿命评估的依据。OCS属于无源光器件,参照无源器件的相关标准[15-19],其与损耗相关的失效模式和失效机理可归纳如表1所示。

表1 OCS的失效模式和失效机理Table 1 Failure modes and failure mechanisms of OCS
回波损耗和偏振相关损耗对OCS的影响较小,为简化分析,本文仅考虑插入损耗IL(Insertion Loss)。类似于磁光隔离器,将OCS的插入损耗定义为:引入OCS所导致的传感光路的功率损耗,即OCS的输出光功率(对应于静态工作光强Ps)与输入光功率P0比值的分贝数,表示为[14]:

根据上式,定义插入损耗变化量ΔAIL为:

其中,Ps0为初始静态工作光强;Ps1为变化后的静态工作光强。
对于选定的光电转换器,其响应度R也确定,则式(10)也可以用静态工作电压来描述:
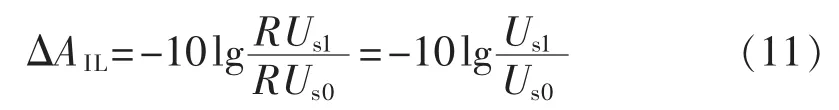
其中,Us0为初始静态工作电压;Us1为变化后的静态工作电压。
插入损耗变化量ΔAIL存在一个允许范围,本文将此允许范围作为OCS的失效判据。当由于外界环境等因素引起的OCS的插入损耗变化量在此范围内时,则认为OCS工作正常;否则认为OCS的性能已遭到破坏,即认为OCS失效。
2.2 失效判据的计算
如图2所示,OCS的输出在进入数字信号处理器(DSP)之前,首先要通过A/D转换器进行A/D转换。为了保证OCS的测量误差满足测量要求,必须要求A/D转换器产生的量化误差不能超过OCS的误差限值。
A/D转换器的最大量化误差表示为[20]:

其中,q为A/D转换器的量化等级,其计算式为:

其中,Vfs为A/D转换器的满刻度量程;N为A/D转换器的位数。
对每个采样样本的量化误差,一般是假设随机和均匀分布于区间(0,q/2)和(-q/2,0)内,所以量化误差的标准偏差(也等于测量宽带量化噪声的均方根值或测量不确定度)可以表示为:

设被测电流i(t)的有效值为Irms,则OCS的测量通道输出信号umx的有效值可表示为:
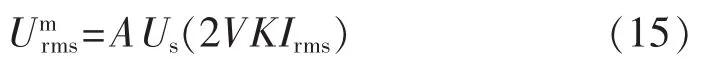
则对于测量通道输出,A/D转换器的量化误差带来的测量误差可以表示为[20]:
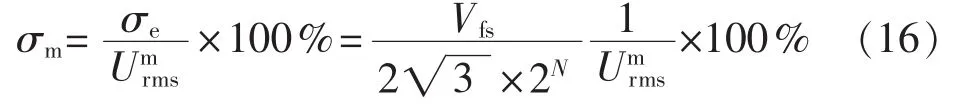
本文设计的OCS选取的A/D转换器的参数为:Vfs=20 V(对应±10 V),N=16。 由式(16),根据0.2S级的OCS的比值误差限值要求,可以求得归算至额定电流下的测量通道输出信号umx的有效值Umrms的允许下限值见表2。
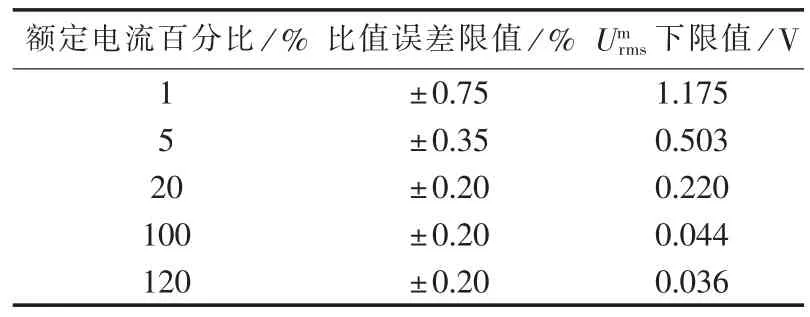
表2 Umrms的允许下限值Table 2 Allowable low limits of Umrms
另外,考虑到测量通道能准确测量2倍额定电流,测量通道输出信号umx的有效值Umrms的允许上限值为3.536 V。所以,测量通道输出信号umx的有效值 Umrms的允许范围为[1.175,3.536]V。
对于设计的OCS,选定磁光玻璃材料、固定设计结构和布置位置,则菲尔德常数V和结构参数K基本确定,对于不同的额定电流,可以通过设计不同的放大倍数A,使得下式成立:

即Umrms的允许范围[1.175,3.536]V就是静态工作电压Us的允许范围。对于保护通道输出,由式(6)可以看出,此上限值显然是满足要求的。下面讨论在此下限值时,其量化误差能否在额定电流下满足±1%的误差要求。
对于保护通道输出,A/D转换器的量化误差带来的测量误差可以表示为:
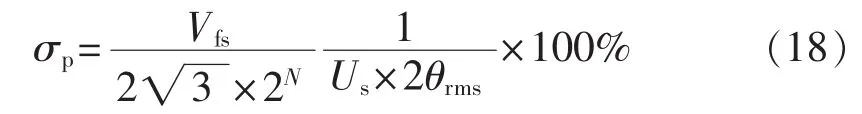
由上式可以求得满足误差要求的Faraday旋转角θ的有效值θrms下限为3.75×10-3rad,对于本文设计的OCS,对应额定电流有效值约为300 A。即对于测量额定电流300 A以上的应用,在Us为1.175 V时,其量化误差能满足OCS保护通道的误差要求。额定电流300 A对于一般应用已满足。
综上所述,本文确定OCS的静态工作电压Us的允许范围即为[1.175,3.536]V。通过调节驱动电流来调节光源的输出光功率P0实现OCS初始静态工作电压Us0的设置,一般使Us0等于允许范围的中间值,即Us0=2.2 V。则由式(11)可得到对应于初始静态工作电压Us0=2.2 V,插入损耗变化量ΔAIL的允许范围为[-2.06,2.72]dB。
3 OCS的加速老化试验
3.1 加速失效模型分析
3.1.1 失效分布
经验表明,无源光器件的损耗失效分布服从对数正态分布[16]。OCS属于无源光组件,其主要失效模式是插入损耗失效,因此,它的损耗失效时间tsx服从对数正态分布,其概率分布函数为:
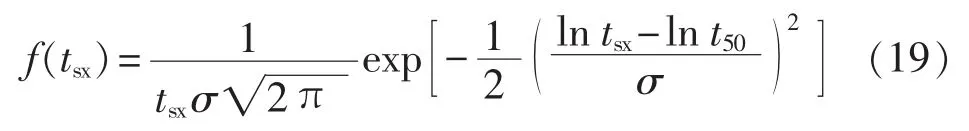
其中,t50为中位寿命,表示50%的样本失效时的时间;σ为ln tsx的标准偏差;tsx为失效时间。
3.1.2 加速失效模型
加速试验是证明OCS长期可靠性所必需的试验。高温、高湿环境寿命试验是在合理的试验时间中提供可靠性数据最常用的方法。本文选择温度作为加速应力。
对于温度热应力,寿命和温度之间的关联是从阿伦尼斯关系衍生出来的[19]:
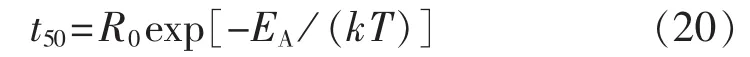
其中,R0为系数;k 为波尔兹曼常数(8.6×10-5eV/K);T为绝对温度(K);EA为激活能(eV)。无源光器件的激活能大约是0.4~1.2 eV,高温无湿度的试验环境下,OCS的激活能保守地选择为0.4 eV。
3.1.3 加速系数
以温度热应力为例,根据式(20),定义OCS寿命试验的相对加速系数为:

其中,t1和t2分别为温度T1和T2下的中位寿命。
3.2 加速试验方案设计
参照无源光器件的可靠性相关标准的抽样程序和抽样表[17],选定参加加速试验的OCS样本数为20,则产品质量的不合格率极限水平不超过15%;选择温度T=85℃作为加速热应力;选择插入损耗变化量ΔAIL的允许范围[-2.0,2.7]dB作为OCS的失效判据。
图3所示OCS加速试验系统主要包括LED光源、传输光纤、OCS样本、采集器、温控箱和监测软件平台。OCS样本放置在试验平台的温控箱内部,接受高温加速老化试验。对每个OCS样本,LED光源发出光功率为P0的光信号通过传输光纤进入OCS的输入端,OCS输出的光功率为Ps的光信号再通过传输光纤输入采集器的光电转换器,得到其静态工作光强Us,采集器的A/D转换器对Us采样后输入PC机,PC机的监测软件平台对数据进行实时监测和存储。
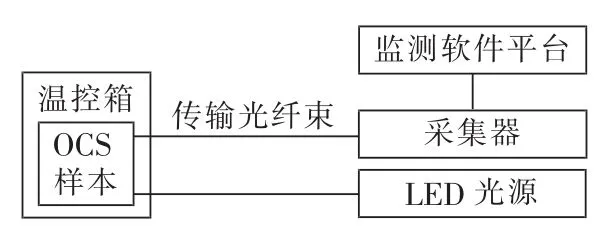
图3 OCS的加速试验系统Fig.3 Accelerated test system for OCS
通过调整LED光源发出的光功率,使得每个OCS样本的初始静态工作电压均在2.2 V附近;设置温控箱的温度稳定工作在85℃;监测软件平台对静态工作电压进行连续实时监测,设置每隔15 min进行一次数据记录,并以Excel表格的形式进行数据存储。
4 OCS的寿命评估
4.1 中位寿命计算
在加速老化试验过程中,不可能所有样本都达到失效水平,通常需要推断失效水平的趋势。对于无源光器件,一般可以采用线性推断的方法[19]。
图4(a)为由监测数据得到的6号样本的插入损耗随时间的变化曲线图,根据变化趋势,可以通过线性外推(图中虚线所示)得到6号样本的失效时间为2350 h。图4(b)为由监测数据得到的2号样本的插入损耗随时间的变化曲线图,可以看出该样本没有失效的趋势,此时将其失效时间先标记为“不明显”,但是可以肯定它的失效时间也是服从统计规律的。
依照上述方法,对其他样本监测获得的静态工作电压监测数据进行分析,得到表3所示的20个OCS样本的失效时间。为了方便中位寿命的计算,表中所列样本序号按照失效时间重新进行了升序排列。
绘制试验样本监测数据的对数正态图,其具体方法如下[19]。

图4 样本插入损耗变化量曲线Fig.4 Insertion loss variation of samples
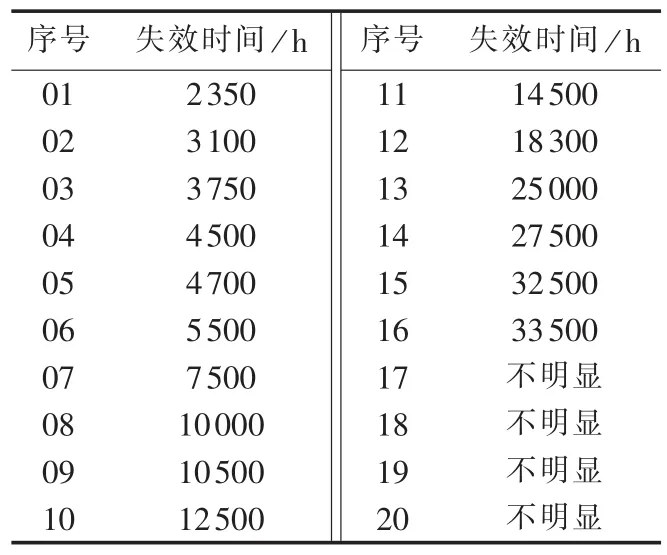
表3 样本的失效时间Table 3 Time to failure of samples
a.取表3中根据升序排列的失效时间的自然对数ln tsx作为y轴的值。
b.将试验样本总数M和表3中样本序号m代入 NORMSINV[m /(M+1)]作为 x 轴的值,NORMSINV为标准正态累积分布函数的反函数。
c.在坐标图中描出16个点(因为有4个样本失效时间不明显),根据最少拐弯原则拟合出最匹配的直线,其方程表达为:

其中,t50和σ与式(19)中含义相同。
图5为按照上述过程得到的样本在85℃试验条件下的对数正态图。从图中可以看出,有确定失效时间的样本点近似线性。由于OCS失效时间服从对数正态分布,说明失效时间不明显的样本点也会在该拟合直线的延长线上。由确定的样本点拟合后的直线方程为y=1.241x+9.562,拟合系数为0.974。可以算得,在85℃ 试验条件下,OCS的中位寿命t50为14217 h,ln tsx的标准偏差为1.241。

图5 失效时间的标准正态分布Fig.5 Standard normal distribution of time to failure
由式(21)可以得到,OCS在试验温度为85℃时对应于常态温度25℃时的加速系数 τ为13.6,则可以得到常态温度25℃条件下,OCS的中位寿命为193358 h,约合22 a。此22 a即为基于本文设计的加速老化试验得到的OCS在常态温度下的预计使用寿命。
4.2 置信度分析
预计使用寿命的置信度与样本的试验条件、试验时间和样本数量息息相关。
要求OCS在常态温度下使用寿命为22 a的置信度p为0.95时,推算在加速温度为85℃的试验条件下对20个OCS样本的试验时间。推算过程如下。
(1)考察寿命:
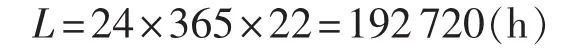
(2)置信度系数:
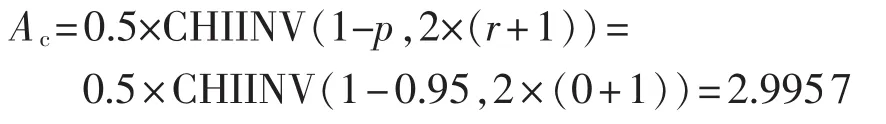
其中,CHIINV为卡方分布符号;r为允许失效数,本文取为0。
(3)常态测试时间:

(4)加速试验时间:
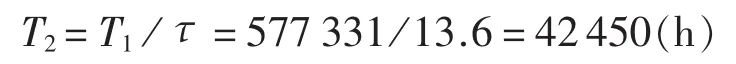
(5)单台试验时间:
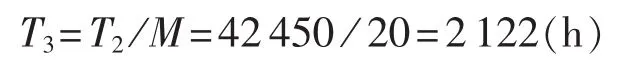
由上述过程可知,在加速温度85℃的试验条件下,如果对20个样品进行1次实验,需持续2122 h,大约为88 d。
本文对20个OCS样本从2013年4月22日至7月21日进行了连续90 d的85℃试验条件下的加速老化试验,所以本文推算出的OCS在常态温度下的22 a的预计使用寿命的置信度为95%。
5 结论
a.分析了基于Faraday磁光效应原理的OCS的失效模式和失效机理,提出了OCS插入损耗变化量的概念,并以此作为OCS失效判断的依据。
b.从A/D转换器带来的量化误差引起OCS测量误差的角度出发,分析和计算了0.2S级OCS的插入损耗变化量的允许范围,并以此作为OCS的失效判据对试验数据进行了分析。
c.将OCS看作一种无源光器件,以温度作为加速应力,设计了OCS的加速老化试验方案,对随机抽取的20个OCS样本在85℃的高温下进行了90 d的热老化试验。
d.对样本试验数据进行了分析,计算了OCS的中位寿命,得到了OCS在常态温度下的预计使用寿命,并对此预计使用寿命的置信度水平进行了分析。分析结果表明:在95%的置信度水平下,本文设计的OCS在常态温度下具有22a的预计使用寿命。
