基于井下异构无线传感器网络DV-Hop定位算法的改进

方旺盛, 吴胜宝

(江西理工大学 信息工程学院, 江西 赣州 341000)

0 引 言

我国矿产资源丰富，而矿井安全技术比较落后，事故隐患多，因此，提高安全生产和监测是一个必需而且很迫切的要求。由于无线传感器节点的灵活性和多样性，经防爆处理和技术优化后，可用于危险工作环境中的实时监测,有着广阔的应用前景[1]。而传感器节点定位又是安全监测最核心的问题，近些年来有很多关于井下的无线传感器节点定位算法研究，大致分为两大类：基于测距和非测距，前者利用电磁波的衰减规律或速度来测距，如接收信号强度指示 (received signal strength indication，RSSI)、到达时间(time of arrival，TOA[2])等；后者是利用网络的拓扑结构来转换为实际距离，如DV-Hop、质心算法[3]等。而井下环境情况复杂多变，巷道弯曲，通信条件差，存在明显的多径效应[4],基于测距的定位算法并不太适合,且节点都是按需随机部署的，不能保证节点密度[5]，因此,有必要对当前无需测距的定位算法进行改进。梁美玉、李莉等人提出了使用蚁群算法优化误差函数来提高定位精度[6]。刘凯、余君君等人提出了一种信标节点优选方案和跳数加权算法来提高定位精度[7]。杨顺、李龙青利用导标节点和未知节点之间的几何拓扑关系提高定位精度[8]。综上所述，目前对这类算法最主要的改进是在目标原始位置数据采集与滤波[9]，以及在对节点在全局位置进行估计时的估计算法来进行改进[10]。本文从巷道复杂弯曲和节点分布不均匀对井下节点定位精度影响的角度进行分析改进，在DV-Hop算法的跳数选取和平均跳距选取过程中引入了筛选因子，使得筛选出来的平均跳数和平均跳距更加准确，也使该算法更加适合于井下传感器节点的定位。

1 井下隧道物理模型

1.1 井下空间模型

井下巷道根据其空间特性和功能，分为垂直巷道、倾斜巷道和水平巷道三大类[11]。为了研究方便，按空间关系作了一些简化，简化后，可将井下巷道统一划分为多层巷道和分支巷道、弧形巷道，如图1所示。

图1 分层巷道和分支、弧形巷道简化模型

1.2 井下电磁波传输模型

在无线传感器研究中，电磁波在空间中的传播损耗模型分为自由空间传播损耗模型、对数路径损耗模型、屏蔽模型等三类[12]。

然而自由空间损耗模型和对数损耗模型将通信环境描述成理想环境[13]，但是，在矿井中传播的无线电波受到巷道尺寸、拐弯等因素的影响,主要表现在电磁波受发射端与接收端之间的视距和节点覆盖规则的影响[14],因此，这2种模型并不适合本文的研究需要;而屏蔽模型是对理想圆形模型进行了扩展，更加符合矿井中复杂的环境，所以，本文采用的路径损耗模型为屏蔽模型。

屏蔽模型的路径损耗模型使用了一个接近中心的距离r0为参考，对距离为r的平均接收功率P(r)进行预测，两者的比值如式(1)

(1)

式中P(r0)为r0的参考功率值，β为路径衰减指数，一般为实际测量得到的经验值,一般情况下为0.4～0.65。式(1)是电磁波在理想情况下的传输模型，还需考虑信号功率的损耗，经研究测量，无线信号路径损耗功率是对数正态随机变量[15]，因此，可得出井下无线信号传播模型，如式(2)

(2)

其中,φ为一个均值为零的高斯分布变量[16]，没有实际意义，为了计算方便，这里不考虑φ影响，可根据式(1)可推导出通信半径和节点间距离的关系如式(3)所示

(3)

2 DV-HOP算法分析与改进

2.1 传统算法分析

Niculescu D等人提出的DV-Hop节点定位算法是一种基于距离矢量计算跳数的算法[17]。首先，每个信标节点向所在网络广播包含自身位置信息和跳数值为0的信息，当周围邻居节点接收后，将会记录位置信息和跳数，并将跳数加1再广播出去，整个过程中只保留收到的包含最小跳数值的信息，以此类推，直到网络中所有节点都获得与之相邻的信标节点的位置信息和最小跳数值。

其次，当锚节点收到其它锚节点的信息后，可依据式(4)估算平均每跳距离

(4)

式中 (xi，yi) 和(xj，yj)为锚节点i和j的坐标，hj为锚节点j到锚节点i的最小跳数。

2.2 算法改进描述

由于矿井下节点分布不均匀，通信条件比较差，传统的校正值不能对平均每跳距离进行精确估计。如图2所示，井下节点通信半径基本相同，设定R为巷道中锚节点通信半径，当锚节点S(黑色三角形)发送数据时，因为节点通信半径大于巷道宽度，布置在巷道侧壁上的未知节点A和B(白色圆点)都落在节点S的通信半径R内，若按传统方法计算跳数，将会得到相同的跳数，即都为1跳。但是，节点A和节点B距离锚节点S却相差很大，锚节点通信半径越大，相差越大。

图2 巷道中节点位置与通信半径的关系

因此在本文中，跳数值不仅能以整数值1跳递增，也能以小数值0.5跳递增，将锚节点覆盖区域划分为两部分，取通信半径的1/2为区分半径。由式(3)可将距离差值换算成功率衰减程度，如式(5)所示

P(r0)/P(r)=2β.

(5)

当功率衰减程度大2β时，表明此时未知节点与锚节点的距离大于R/2，此时就取跳数值为1;否则,取0.5，如式(6)所示

(6)

前文已经提到，井下隧道有很多支道和弯道，如图3所示，这里给出了井下节点网络基本场景的直线拟合，信标节点N与未知节点A,B,C,D之间的路径近似于直线，但由于井下弯道和设备障碍的存在，在信标节点2,3等之间的路径形成一定的弯曲度,增大了它们之间的可达跳数。

图3 井下场景直线拟合示意图

因此，在计算平均每跳距离avgij时，就需要筛选一个比较精确的平均跳距。以信标节点N举例，给出选择过程的简单描述：

信标节点N与周围的n-1个信标之间有n-1个avgij(j=2,3,…，n)，取其中一个值作为参考对象，若以信标节点2和1之间的跳距avg21为参考，考虑其他n-2个avgi1与其之间的偏差程度，用ρj1表示，如式(7)所示

(7)

则每个偏差度对应的选择因子αj1可由式(8)表示

(8)

从式中可看出：偏差程度ρj1越小，其选择因子αj1越大，因此，选择αj1最大值所相应的avgj1作为信标节点1最终与未知节点之间的平均每跳距离avg1。以此类推，直到其他n-1个信标节点与未知节点之间的平均每跳距离值avgi选择出来，再求平均值，得出最终的平均跳距Cavg

(9)

结合式(6)计算出来的跳数，利用传统计算方法计算出每个未知节点到相邻锚节点的距离

dn=hopsn×Cavg.

(10)

当未知节点至少获得与3个锚节点间的距离时，假设(x,y)为未知节点坐标，它接收到的锚节点坐标为(xn,yn)通过使用最大似然估计法来计算未知节点的坐标，具体计算公式如式(11)所示

(11)

将前n-1个方程减去最后一个方程，再化简成线性方程AX=B形式，可得到3个矩阵A,X,B，如式(12)所示

(12)

再使用标准的最小均差估计方法可以得到未知节点的坐标(x,y),计算公式如式(13)所示

=AT(ATA)-1B.

(13)

3 实验仿真

为了验证区域划分和筛选因子在定位算法改进中的作用，在这里利用Matlab平台上进行仿真实验。为了实验数据更为理想，对每个实验场景都执行了50次，再求平均。因为研究的是井下隧道，故选定仿真区域为5 m×2 000 m的矩形区域，信标节点和未知节点坐标随机产生，节点通信半径相同，仿真结果如图4、图5、图6所示。

图4所示是在相同通信半径情况下,在长直隧道中,改进算法比传统算法定位精度更高,从图中可看出：当通信半径为20～30 m时，定位精度比传统算法提高了20 %。在筛选平均跳数和跳距过程中充分利用节点资源来减少误差，有效降低了节点定位误差。但当半径较小时，改进算法优势不很明显，因为半径太小，就没有分区域的必要。随着通信半径进一步增大时，定位精度提高有所减少，半径太大，误差也大，若再细分区域就会增加节点计算量，就会消耗更多节点能量，这样会影响井下传感器节点的寿命。

图5、图6中是经改进的DV-Hop算法，分别在弯曲巷道和长直巷道以及分层层数不同几种情况下与传统DV-Hop算法的定位误差的比较，可看出定位误差随着锚节点个数的增加而减少,锚节点数量在120～150个时提高最为明显，因为随着锚节点数量的增加扩大了筛选范围，也提高了跳数精度。但不能随意增加锚节点数量，随着锚节点数量的增加，锚节点的计算量会急剧增大，当锚节点数量到了一定数量时，定位精度提高的就趋于平缓了。

图4 锚节点通信半径与平均定位误差的关系

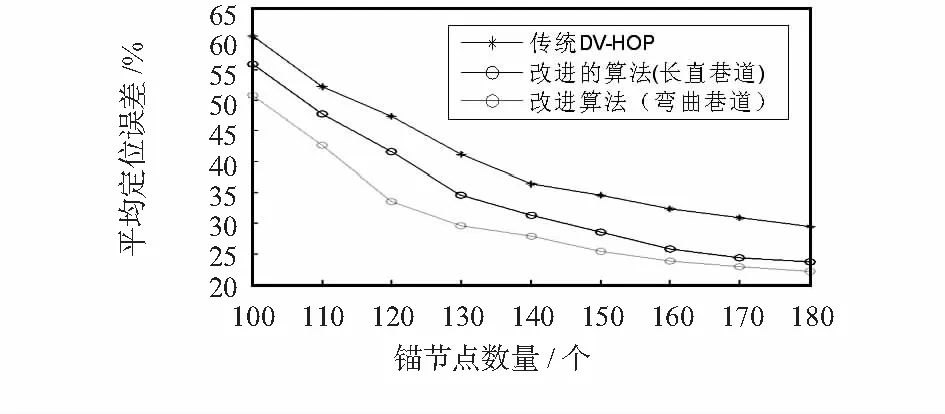
图5 锚节点数量与平均定位误差的关系

综上所述,通过划分信号覆盖区域来提高跳数精确度和采用筛选因子来选择平均跳距的方式能有效提高井下DV-HOP算法的定位精度，尤其是在有弯道和分层的情形下提高更为明显，更加适合环境复杂的井下无线传感器网络节点定位。

4 结 论

针对传统DV-Hop在井下巷道中的局限性，本文结合井下隧道弯曲复杂的特点对传统算法提出了改进，通过划分锚节点信号区域的方法来提高跳数的精准度，以减少定位半径与节点距离相差太大而造成的跳数误差；而在平均跳距选取方面，提出了使用一个选择因子来筛选平均跳距，使得平均每跳距离更加接近于实际值。进而减小由于巷道弯曲所造成的节点间距离的误差。仿真结果表明：在井下巷道有弯曲或者分层情况下，本文的算法比传统DV-Hop定位算法在定位精度上有很大程度的提高，更加适合井下井下复杂环境的节点定位。

参考文献:

[1] 张江石,傅 贵,陈 娜,等.矿工应急处置能力评估方法研究 [J].煤炭学报,2012,37(2):290-294.

[2] 周公博.矿井巷道无线传感器网络分层拓扑控制策略[J].煤炭学报，2010,35(2):333-337.

[3] 薛 霞,孙 勇.监测煤矿的一种无线传感器网络节点定位算法[J].传感器与微系统,2010,29(9):119-123.

[4] Xiao Yi,Yu Lin,Lu Deng.An improved DV-Hop positioning algorithm with modified distance error for wireless sensor net-works[C]∥2009 Second International Symposium on Knowledge Acquisition and Modeling,2009:216-218.

[5] 刘志高,李春文,邢智鹏,等.巷道网络全局定位系统关键技术分析与实验[J].煤炭学报,2011,36 (3):519-526.

[6] 梁美玉,李 莉,陈 坤.基于蚁群算法的井下无线传感器网络节点定位研究[J].煤矿机械,2010,31 (12):48-50.

[7] 刘 凯,余君君,谭立雄.跳数加权DV-Hop定位算法[J].传感技术学报,2012,25(11):1539-1542.

[8] 杨 顺,李龙青.井下无线传感器网络DV-Hop定位算法的改进[J].微电子学与计算机,2010,27 (11):166-120.

[9] 刘文远,王恩爽,陈子军.无线传感器网络中DV-Hop定位算法的改进[J].小型微型计算机系统,2011,32(6):1071-1075.

[10] 赵清华,刘少飞,张朝霞.一种无需测距节点定位算法的分析改进[J].传感技术学报,2010,23(1):122-127.

[11] Han Guorui,Zhang Wenmei,Zhang Y P.An experiment study of the propagation of radio waves in a scaled model of long-wall coal mining tunnels[J].IEEE Antennas and Wireless Propagation Letters,2009(8):502-504.

[12] Madhulika,Kumar A,Varna S.Iterative and distributed range-free localization algorithm for wireless sensor networks [C]∥Proc of IMPACT’09,Aligarh,2009:102-105.

[13] Almuzaini K,Gulliver T A.A new distributed range-free localization algorithm for wireless networks[C]∥Proc of 70th VTC Fall:IEEE,Anchorage,AK,2009:1-5.

[14] Bettstetter C.On the minimum node degree and connectivity of a wireless multi-hop network [C]∥MOBIHOC’02,New York,US:ACM,2002:80- 91.

[15] Poggi C,Mazzini G.Collinearity for sensor network localiza-tion [C]∥Proceedings of 2003 IEEE 58th Vehicular Technology Conference Piscatataway,NI,USA,IEEE,2004:3040-3044.

[16] Huang Qiqian,Selvakenndev S.A range-free localization algorithm for wireless sensor networks [C]∥Proc of 63rd Vehicle Technology Conference:IEEE,Melbourne,Vic,2006:349-35.

[17] Niculescu D,Nath B.DV-based positioning in Ad Hoc network-s[J].Journal of Telecommunication Systems,2003,22(1/4):267-280.