矩形柔性涡流阵列传感器裂纹检测研究*

杜金强, 何宇廷, 李培源

(空军工程大学 航空航天工程学院,陕西 西安 710038)

0 引 言

飞机结构是飞机装备的载体，是飞机在使用期限内满足规定功能和任务需求的基础。飞机结构在使用过程中难免会出现疲劳损伤，若机体主承力结构上出现的疲劳裂纹不能被及时发现并加以修复，将会导致灾难性事故[1]。长期以来，无损检测技术在飞机使用维护中发挥着极其重要的作用，但随着飞机结构形式日趋复杂、使用强度不断增加、服役使用寿命不断延长，仅依靠传统的无损检测技术难以保证飞机使用安全[2]。结构疲劳损伤监测技术可显著提高飞机结构安全性，开展飞机结构疲劳损伤监测技术研究，对保证飞行安全具有重要意义[3]。

电涡流检测技术适用于大多数导电材料的损伤检测，具有使用范围广、易于与结构集成、能够进行结构应力和疲劳裂纹检测等优点[4～6]。而目前大部分飞机的主承力结构是金属结构，显然电涡流检测技术在飞机结构疲劳损伤检测领域具有巨大的研究价值和应用潜力。

一种矩形涡流阵列传感器可用于金属结构裂纹的定量检测，精度约为1 mm。但是在裂纹检测过程中，提离效应往往会对裂纹检测产生影响。本文通过建立矩形涡流阵列传感器的有限元模型，分析了传感器对提离距离的响应特性，并搭建模拟裂纹检测试验平台，研究了提离距离对传感器裂纹检测能力的影响。

1 用于裂纹检测的矩形涡流阵列传感器

矩形涡流阵列传感器由一个激励线圈和多个均匀分布于激励线圈两侧的感应线圈构成，如图1所示[7]。检测裂纹时，在驱动电流的作用下，激励线圈周围产生周期性分布的电磁场，感应线圈接收激励场在检测空间内的反射场。其中对反射场影响最大的是感应线圈覆盖区域下材料的电磁特性参数和边界条件。在其它条件不变的情况下，当结构损伤扩展到感应线圈I的检测区域时，其输出信号会发生变化，当结构损伤扩展到感应线圈II的检测区域时，其输出信号也会相应地发生变化，通过检测各感应线圈的信号变化情况，结合感应线圈的空间位置，就可以实现对裂纹的定量检测。

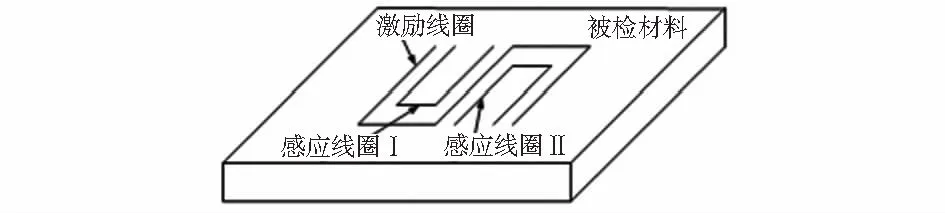
图1 矩形涡流阵列传感器

当裂纹损伤进入某感应线圈的检测区域时[8]，其输出信号幅值开始快速增加(图2中A点)，随着裂纹的扩展，幅值持续增加；当裂纹穿过该感应线圈时，其输出信号将趋于稳定(图2中B点)。显然通过算法扑捉A，B这2个特征点就可以实现裂纹的定量检测。但在某些因素影响下，当A,B点所对应的输出信号幅值差ΔU较小时，特征点的扑捉将变得相对困难，从而制约裂纹的检测。因此，传感器的裂纹检测性能可以通过ΔU的大小来进行衡量。

图2 矩形阵列传感器输出信号的特征

2 提离响应特性的有限元分析

1)传感器的物理模型

涡流阵列传感器的物理模型主要由涡流阵列传感器和金属平板组成，如图1所示。被测金属平板的材料为2A12—T4铝合金，大小为30 mm×30 mm×4 mm(长×宽×厚)，在平板的上方放置了经过简化的涡流阵列传感器，由一个激励线圈和2个感应线圈构成，其中,线圈的材料为黄铜，线圈平面与被测金属平板之间的间距为0.1 mm。

2)传感器的有限元建模

有限元分析软件ANSYS的Emag和Multiphysics模块具有强大的电磁场分析功能，可以进行二维、三维稳态、谐波和瞬态磁场分析，能够对工程电磁场问题进行数值模拟和分析[9]。本文运用该软件来建立模型，为了详细反映空间的电磁场分布，建立了三维有限元模型。在建模过程中，采用SOLID97单元来表征铝合金平板、线圈阵列和空气域，采用CIRCU124单元施加外电路激励(如图3(a),(b)所示)。给平板、线圈和空气域分别赋予不同的材料特性，然后划分网格。为了保证计算精度，同时节省计算时间，采用六面体和四面体混合的网格划分方法，最终建立的有限元模型如图3(c)所示。

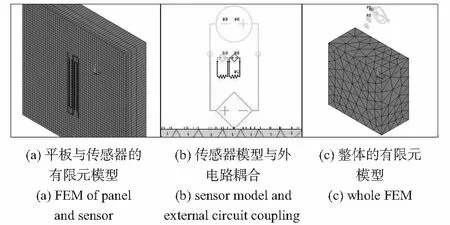
图3 涡流阵列传感器裂纹检测的有限元模型

为了满足ANSYS有限元仿真中区域必须为封闭区域的条件，给有限元模型中空气域的外边界加载了平行边界条件。同时，通过外电路为激励线圈加载了幅值为1A、归一化频率为0.3、初相位为0°的正弦激励信号,然后进行谐波分析(采用Sparse求解器进行求解);最后通过后处理模块得到了磁矢位A在传感器平面内和横截面内的分布情况(如图4所示)，可见磁矢位的分布关于激励线圈导线中心对称，在激励线圈导线中间达到最大值，这与文献[10]中的分析结果是一致的。

图4 磁矢量位A的分布情况

3)传感器对提离距离的响应特性分析

对矩形阵列传感器施加正弦激励信号，激励电流的幅值为1A，归一化激励频率为0.3，初相位为0°。运用建立的有限元模型，分析了提离距离分别为0.1,0.2,0.3,0.4,0.5,0.6,0.7 mm时传感器的输出信号，由于各感应线圈输出信号相同，本节仅对感应线圈I输出信号的幅值和相位进行了分析，如图5所示。

可见随着提离距离的增加，传感器输出信号的幅值和相位信号均显著增加。当提离距离从0增加至0.7 mm时，幅值信号增加了约25 mV，增加幅度约为73.5 %；相位增加了约10°，增加幅度约为12.6 %，显然矩形阵列传感器对提离距离十分敏感。相比之下，矩形涡流阵列传感器在裂纹检测中，出现裂纹前后感应电压幅值的增加幅度也仅仅为5 %左右，显然裂纹检测过程中，提离效应会对检测结果产生严重影响。

图5 矩形阵列传感器在不同提离距离时的响应特性

3 提离距离对传感器裂纹检测影响

1)模拟裂纹检测试验方案设计

在金属板材上制作一条长的模拟裂纹，通过传感器在试验件表面的平稳相对滑动来模拟裂纹的扩展过程，如图6所示。本文中所使用的金属板材为2A12—T4铝合金，试样尺寸为190 mm×50 mm×4 mm，试样的长度方向垂直于轧制方向，通过线切割在试样中间位置制作了一条长为50 mm、宽度为0.2 mm的穿透裂纹。

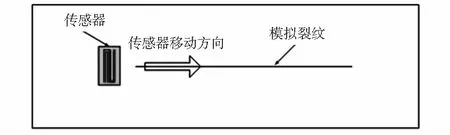
图6 裂纹扩展的模拟过程

为实现对2A12—T4铝合金裂纹的检测，搭建了检测系统，完成信号发生、传输、采集、特征提取的全过程。裂纹检测实验系统主要由激励信号源、功率放大器、矩形涡流阵列传感器、多功能试验台、信号采集系统与信号处理系统六大部分构成。其中多功能试验台主要由高精度数控三轴平移台组成，用来驱动传感器在被检材料表面平稳移动。将传感器固定于多功能试验台安装座上，通过平移台将传感器压紧于试验件表面，并给传感器施加归一化频率为0.3的正弦激励信号；然后将传感器沿着裂纹长度方向移动，模拟裂纹的扩展过程，测量不同裂纹长度时传感器各感应线圈的输出信号(在裂纹检测中，特征信号为幅值信号[8])。

2)试验结果与分析

在传感器和试验件之间放置不同厚度的标准膜片，模拟不同提离距离的情形。本文分别对传感器和试验件之间无提离、归一化提离距离为0.5、归一化提离距离为1的3种情况，进行了模拟裂纹的检测试验，裂纹每“扩展”0.2 mm采集一次感应线圈的幅值信号。鉴于传感器各感应线圈的输出特性基本一致，仅对感应线圈I的输出特性进行了分析，该感应线圈可以对0～1 mm长的裂纹进行检测。为便于进行不同提离距离时传感器裂纹检测性能的对比，定义涡流阵列传感器感应线圈I的幅值变化率为

(1)

式中rj为感应线圈在裂纹长度为jmm时的输出信号幅值，r0为感应线圈在裂纹长度为0 mm时的输出信号幅值。

图7为不同提离距离时传感器的裂纹检测特性，其中图7(a)为幅值变化率随裂纹长度的变化情况，可见随着裂纹的扩展，感应线圈的输出信号幅值逐渐增加，当裂纹穿过感应线圈的监测区域后，幅值信号的增加幅度逐渐放缓，并在裂纹长度约为1.5 mm左右时达到最大值，当裂纹进一步扩展时，传感器的信号不再明显变化。在裂纹扩展并穿过感应线圈检测区域的过程中，随着提离距离的增加，幅值信号的增加幅度急剧减小。图7(b)为在裂纹从0 mm扩展至1 mm过程中，幅值变化幅度随提离距离的变化情况，可见随着提离距离的增加，幅值变化幅度急剧减小，相应地裂纹检测能力变弱，当归一化提离距离增加至1时，裂纹检测能力降低了约68.1 %。因此,在裂纹检测过程中，必须尽量减小提离距离。

图7 不同提离距离时传感器的裂纹检测特性

4 结 论

1)矩形涡流阵列传感器对提离距离十分敏感，当提离距离从0增加至0.7 mm时，幅值信号增加幅度约为73.5 %，

相位增加幅度约为12.6 %，因此,在裂纹检测过程中要尽量抑制提离距离的波动。

2)提离距离的增加会急剧地降低传感器的裂纹检测能力，当归一化提离距离从0增加至1时，裂纹的检测能力降低了约68.1 %，因此,必须尽量减小提离距离。

参考文献:

[1] 杜洪增.飞机结构疲劳强度与断裂分析[M].北京：中国民航出版社，1996.

[2] 陈志伟,王 智.军用飞机结构疲劳寿命研究[J].机械强度，2005，27(3)：381-387.

[3] 袁慎芳.结构健康监控[M].北京：国防工业出版社，2007.

[4] 李家伟，陈积懋.无损检测手册[M].北京：机械工业出版社，2006.

[5] 韩亚利，陈 勇，周志平.应用涡流电导率检测技术评定铝合金的热损伤[J].航空精密制造技术，2006，42(3)：37-40.

[6] 张思全，陈铁群，刘桂雄.应力腐蚀裂纹涡流检测信号的处理及形状重构[J].核动力工程，2008，29(6)：50-53.

[7] 焦胜博．基于涡流阵列传感器的金属结构裂纹监测方案可行性研究[J]．传感器与微系统，2013,32(8):43-46.

[8] 杜金强．基于电磁涡流的飞机金属结构疲劳损伤监测关键技术研究[D]．西安：空军工程大学，2012.

[9] 阎照文.ANSYS10.0工程电磁分析技术与实例详解[M].北京:中国水利水电出版社，2006.

[10] Nail Jay Goldfine.Uncalibrated,absolute property estimation and measurement optimization for conducting and magnetic media using imposedω-kmagnetometry[D].Cambridge:Massachusetts Institute of Technology,1990.