基于物联网感知层的节点连通算法*

李 娜， 薛建生

(辽宁大学，辽宁 沈阳 110036)

0 引 言

在目前的物联网(IoT)的三层结构中，对数据的处理过程是：感知层感知获取信息，网络层通过网关与互联网等连接[1]，将感知到的数据送到云端进行处理，进而为不同的应用提供服务[2]。由于有些设备功能简单，不能单独完成全部处理工作，所以,数据都需要传送到网关[3]。由于物联网中拥有海量数据，用传统的数据处理模式会造成网络负载加重，影响传输速率甚至造成网络拥堵，因此,有必要改进数据上传的模式，将数据分类分层传输，将物联网中实时性要求高，处理上要求相对比较简单的任务，由感知层设备协同处理，以节省网络带宽，提高处理速度。

本文提出一种基于物联网感知层的设备连通算法，为感知节点的协同工作提供必要的理论基础。

1 基于感知层的节点连通算法

将感知层获取到的数据分为两类进行处理：对于处理上较复杂的数据，仍然通过网关上传云端处理；而对于实时性要求严格且处理上比较简单的数据，不再传输到网关，而是在有处理能力的设备上进行数据处理、融合、去除脏数据。这样不但可以减少向上层传输的数据量，同时能够提高对于实时数据的处理速度[4]。为了实现对实时任务的快速协同处理，感知层众多设备必须快速建立连通关系。嵌入式中间件能够屏蔽掉各个异构网络之间的差异，方便异构设备之间协同工作和数据交互，加强感知节点的互联互操作能力。

将物联网抽象为无向图，运用连通支配集构建节点连通通道传递信息。运用连通支配集不但降低所需维护的路由信息量[5]，还可以优化路由路径[6]，节省连通建立所需时间。对实时数据及时处理，减少因上传数据造成的网络拥塞。

1.1 通过邻接矩阵确定支配集节点

物联网的拓扑结构可以通过无向图表示，各个节点之间的连接情况能够用邻接矩阵的方式表示出来。邻接矩阵生成具体步骤如下：

1)首先选取10个设备作为基础网络，建立其的邻接矩阵，令N=10。

2)将矩阵初始化为元素全为2的矩阵，初始元素下标都赋值为0。

3)判断该矩阵元素下标，若是对角线元素,则转到步骤(4);否则,转到(5)。

4)给对角线上元素赋值为0。

5)给非对角线上元素赋值，根据设备之间是否有连接赋值为1或者0。

6)判断元素下标是否都为N-1，若是，则转到(7);否则,下标加1，转到(3)。

7)向基础网络中添加新设备，令N=物联网系统中节点的个数，转到(3)。

8)算法结束，得到物联网的邻接矩阵。

1.2 构造支配集

如果将物联网的拓扑结构用无向图表示，那么提取关键节点的问题就等同于在图结构中求支配集问题[7]。求支配集的算法的具体步骤如下：

1)通过计算每行或每列的1的个数可以得到节点的邻居节点个数。

2)给所有节点着色为白色。

3)计算每个非黑色节点的活跃邻居节点个数。

4)选取其中个数最大的节点，给其着色为黑色，其邻居节点中的白色节点着色为灰色。

5)判断是否所有节点都为黑色或者灰色，若是,则转到(6);否则,转到(3)。

6)算法结束，输出结果，得到一个支配集。

1.3 检查与实现连通

上一节中得到的支配集节点，连接了所有非支配集节点，但是由于支配集中的节点之间不一定连通，还需要进行检查。具体步骤如下：

1)将得到的邻接矩阵，赋值求幂矩阵和幂次与矩阵，设初始值i=0。

2)判断i是否小于等于N，(N为节点总数目)，若是，则转到(3)；否则，转到(7)。

3)当前用求幂矩阵与最初的矩阵相乘，将得到的新矩阵值赋给求幂矩阵。

4)将求幂矩阵和幂次与矩阵中的元素进行或运算，并赋值给幂次和矩阵。

5)判断中每个元素是否都是非零元素，若是，则转到(6)；否则，i++，转到(2)。

6)该物联网节点间是连通的，算法结束。

7)该物联网节点间是非联通的，算法结束。

如果支配集为非连通的，则需要通过向非连通支配集中加入尽量少的节点使支配集成为连通支配集。具体步骤如下：

1)判断所构造的支配集是否是连通的。

2)计算每个非支配集内的节点与支配集内节点相连的度数。

3)选择其中度数最大的节点并加入到支配集中。

4)判断新构成的支配集是否连通，若连通，转到(5)；否则，转到(2)。

5)得到了连通支配集，算法结束。

1.4 感知节点数据传输过程

假设物联网结构如图1所示，其中节点A和G要协同进行数据处理工作。其中圆圈代表节点，节点之间的直线代表节点之间能够通信。

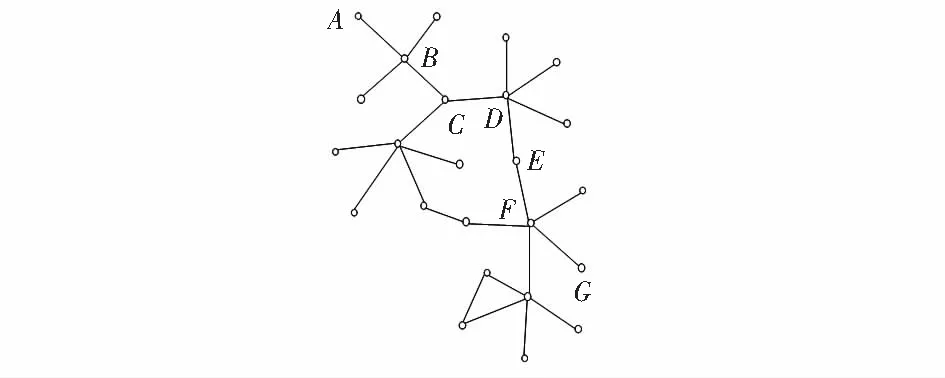
图1 物联网结构图

1)通过将物联网抽象为邻居矩阵，根据度数大小的比较选出物联网中的支配集节点，涂为黑色，如图2所示。

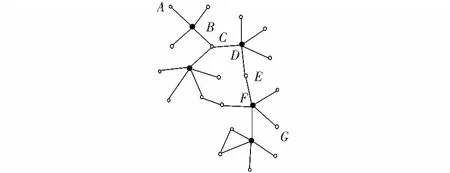
图2 选出支配集节点

2)根据基于矩阵幂次和的连通性判断算法，得出本物联网不连通，将节点C，E移到支配集中，此时各节点之间实现连通。

3)如图3，节点A向节点G发送连接消息，路径为A—B—C—D—E—F—G。

4)节点G向A回复确认，路径G—F—E—D—C—B—A。

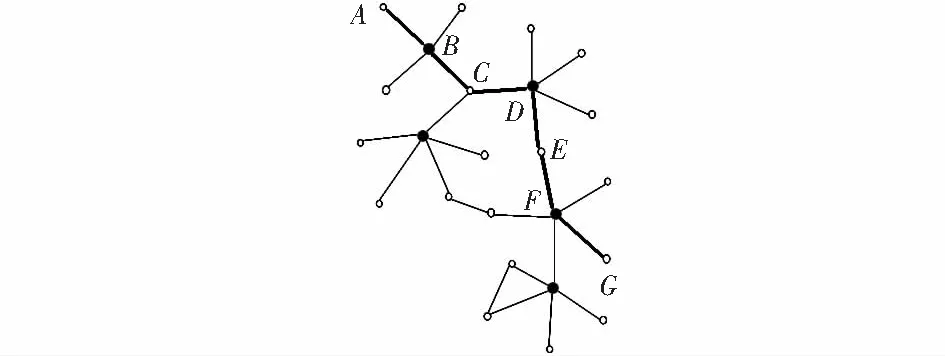
图3 节点A和G之间数据传输路径

2 实验评估与分析

通过在VC++6.0上运用连通算法，对于物联网中的设备个数与生成的支配集中节点个数和建立连通所需时间的关系统计如表1所示。

通过表1可以看出：支配集中节点的个数和建立连通所需时间都随着系统中设备的个数增多而线性增大。根据以上数据，测试环境中设备个数为1 000，对于不同的节点之间，通过中间件屏蔽异构特性，采用统一字符模式。假设节点每次发送数据量为1 kbps，通信带宽256 kbps ，以文献[9]中相关资料为基础，通过统计物联网中实时数据传输总量与两种处理策略中传输总时间的关系，对两者进行比较，结果如图4。

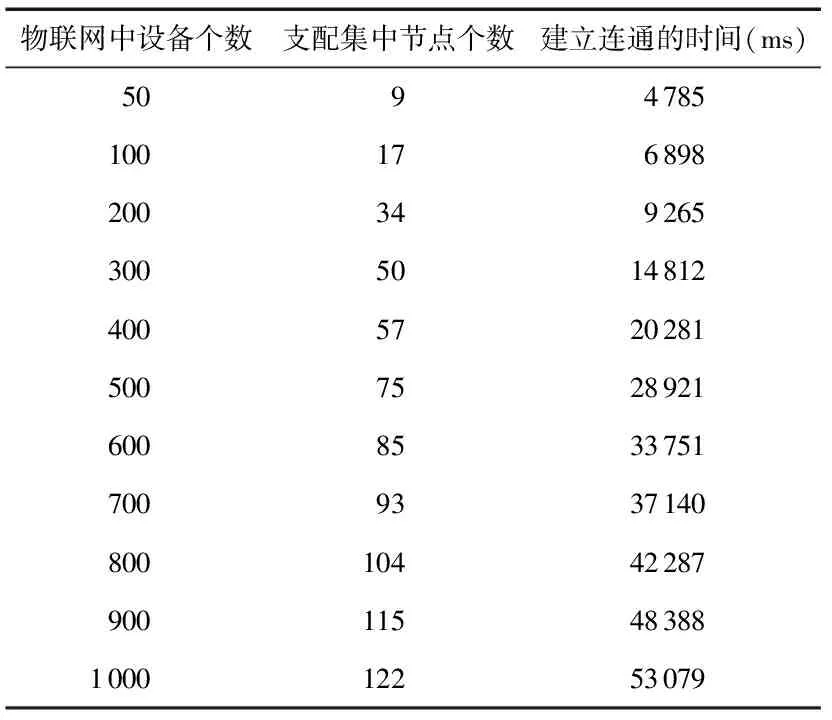
表1 设备个数与支配集中节点个数和建立连通所需时间的关系

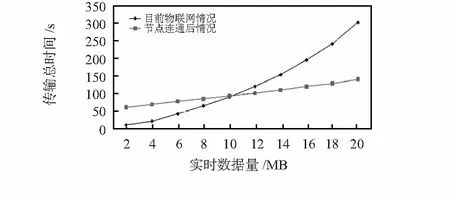
图4 目前的物联网和节点连通后对实时数据传输总时间比较

无线传输技术以Zig Bee为例，具有16条信道。假设物联网中感知层设备能够协同处理的数据占总数据量的1/10。以文献[9]中关于拥堵发生概率分析为依据，对感知层设备连通前后的拥堵情况进行比较，结果如图5。

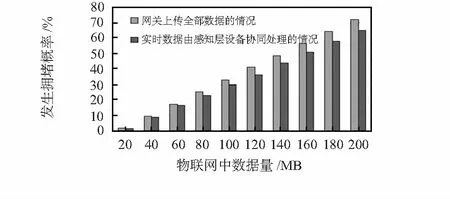
图5 感知层设备连通前后发生拥堵的概率比较

假设节点的初始能力为1 J[9]，采用文献[10]中，接收1位数据所消耗的能量为Eelec=50 nJ/bit，空闲侦听时节点消耗能量为0.88 mJ/s[10]，对建立连通前后节点剩余能量情况进行比较，结果图6。

图6 感知层设备连通前后节点能耗的比较

实验证明:随着物联网规模和传输数据量的增加，通过连通算法将感知层设备连通，协同处理操作上不太复杂的实时数据，在连通建立过程中消耗了一定的时间和能量，但是连通建立之后，时间和能力的开销都减小，总体上来看,通过牺牲少量的能耗节省了大量数据传输时间，有效减低了网络拥堵。

3 结 论

本文将连通算法运用到物联网感知层节点，使设备之间能够协同工作，共同处理简单的实时性任务。选取连通支配集节点，使所要经过的节点数目尽量的少，节省了连通建立所需时间。在网络中信息量增加的情况下，感知层节点连通，减少了数据传输的时间和向网关传输的数据量，降低网络负载，提高网络效率。

参考文献:

[1] Gustavorg,Mario Mo,Carlos D K.Early infrastructure of an Internet of things in spaces for learning[C]∥Eighth IEEE Internatio-nal Conference on Advanced Learning Technologies,2008:381-383.

[2] 周洪波.物联网：技术、应用、标准和商业模式[M].2版.北京：电子工业出版社，2011.

[3] 姜 申.基于物联网的智能电冰箱信息化设计[J].物联网技术,2011(10)：36-40.

[4] 刘源潮.无线传感器网络拓扑中连通支配集的研究[D].苏州：苏州大学，2013.

[5] 张 军.关于无线传感器网络的虚拟骨干网构造算法的研究[D].成都：电子科技大学,2011.

[6] 唐 勇，周明天.基于极大独立集的最小连通支配集的分布式算法[J].电子学报，2007,35(5):868-874.

[7] Gao B,Yang Y,Ma H.A new distributed approximation algorithm for constructing minimum connected dominating set in wireless Ad Hoc networks[J].International Journal of Communication Systems,2005,18(8):743-762.

[8] 李宏波.物联网传输及网络可靠性研究[D].成都：电子科技大学，2012.

[9] 李巧勤，刘 明，杨 梅，等.负载相似节点分布解决传感器网络能量漏洞问题[J].软件学报，2011,22(3):451-465.

[10] Medidi M,Zhou Y.Extending lifetime with differential duty cycles in wireless sensor networks[C]∥Proc of the IEEE Global Telecommunications Conf(GLOBECOM),2007:1033-1037.