RBFNN在速度传感器异常值滤除中的应用

王 静, 李晓林

(太原理工大学 信息工程学院，山西 太原 030024)

0 引 言

异常数据是指在某些特征上明显偏离自身所在集合其他数据的数据,异常数据检测就是辨识这些数据的过程[1]。异常值检测的传统方法是借助图形化工具进行人工检查，但这样的方式不适用于长时间不间断生产的过程工业。近年来，在这一领域发展出一些基于统计理论或机器学习的异常检测方法，如最小体积椭圆法[2]、最小协方差似然估计器[3]、最近邻聚类法、支持向量机分类器等[4,5]。

这些方法各有优缺点：最小体积椭圆法在收集样本后进行异常检测, 适合离线分析; 最小协方差似然估计器应用于非稳态过程的异常检测, 仍是一种离线分析方法; 最近邻聚类法运算复杂度高, 但及时性不足;支持向量机需要对未知情况进行预分类。针对传感器数据连续积累、实时更新的特点，本文提出基于径向基函数神经网络(radial basis function neural network,RBFNN)的异常值滤除。利用前时刻的数据进行神经网络训练,预估下一时刻的传感器测量值,并根据实际测量值是否落入置信区间判断数据是否异常。这种方法的优势在于由数据驱动,无须事先建立过程的机理模型; 同时,该方法仅利用最近的局部数据, 运算量较小, 具有在线应用的潜力[6]。

1 异常数据识别

速度的延滞特性，为基于RBFNN预估数据提供了基础。由前n时刻的值去预估下一时刻的值，与实测值进行比较并判断是否落入由网络训练误差决定的置信区间，以达到异常数据判别。方法具体步骤如下：

1)在k时刻选取前N个数据作为训练集，利用其中n个值Dt(dt-n,dt-n+1,…,dt-1)作为训练输入，选择dt为目标输出训练神经网络。

2)训练结束后，对下一时刻dt+1值做出预估得出预估值pdt+1。

3)将dt+1与pdt+1进行数据比对，如果dt+1落入了以pdt+1为中心的置信区间，则认为数据为正常值。置信区间的选择由高斯概率函数确认,如果没有落入置信区间，则认为数据异常，并剔除异常数据。

4)如果数据正常，代入实测值dt+1，生成新的Dt+1(dt-n+2,dt-n+3,…,dt+1)；如果数据异常则以pdt+1代替dt+1；进行下一步pdt+2的预估,并重复以上步骤(1)～(3)。

具体流程图如图1所示。

图1 实时检测判断

2 速度传感器

工业速度传感器包括很多种类：基于红外测速、雷达测速、超声波测速等的非接触式速度传感器；此外，还有传统的接触式速度传感器，如矿用皮带测速、纸张生产中测速和塑胶、电池等行业测速用传感器。但无论是接触性测速还是非接触性测速，所有的速度值都是一个迟滞性变量，不会瞬间突变，这也是径向基函数预估值判断的原理[7,8]。

本文中以山西某厂家所生产的矿用皮带秤速度传感器为例。该速度传感器利用电磁感应原理，将输入运动速度转换为感应电势输出传感器。它不需要外接电源、结构简单、零位性能稳定。

3 径向基函数原理

3.1 RBFNN预估原理

广义神经网络模型[9]如图2所示。

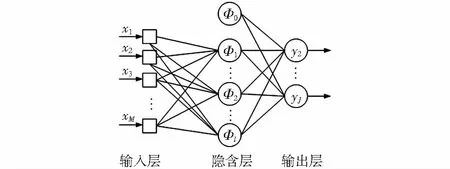
图2 广义神经网络模型

在人工神经网络中，节点对应图中的节点，权值表示节点之间的相互关联强度。网络将知识存储在调整后的各权值中，所以,权值的求取是整个神经网络的关键。

预估计输出Yc(y1c,y2c,y3c,…,ymc)，其值为

(1)

隐含层基函数为高斯函数

(2)

其中,‖xk-xj‖为欧几里德距离，且

‖xk-xj‖2=

(3)

式中w为RBFNN的权重，σ为标准差，按照下式选取

(4)

式中dmax为所选取的中心最大距离，n为隐含节点的个数。

3.2 网络训练

神经网络的训练目的是求取隐含层与输出层之间的权重关系。RBFNN属于有监督学习方式,每一个样本都对应一个教师信号作为期望输出，训练时计算实际输出与期望输出之间的误差，再根据误差的大小和方向对网络权值进行调整,这样的调整反复进行，直到误差达到预期的精度为止。整个网络形成了一个封闭的闭环系统,误差可以使用各输出节点的误差均方值来衡量,这样就建立了一个以网络权值为自变量，最终误差性能为函数值的性能函数，网络训练转换为求解函数最小值的问题。

本文利用Matlab神经网络工具箱中的NEWRB函数自动构建的神经网络[10]。此处取k时刻前的8个历史值作为输入，故存在8个输入。以NEWRB网络默认构建25个隐含层节点。如图3所示。

图3 RBFNN结构

根据径向基函数中心确定方法的不同，在此处采用随机选取固定中心的方式进行网络训练[11]。这种方式能防止径向基函数出现太平或太尖的情况;并且基函数的中心和标准差都是固定的，唯一需要训练的参数就是隐含层与输出层之间的权值。

在本文中实验数据来自山西某煤矿主井主皮带速度传感器1 min内的120组采样数据。表1中列出了部分数据值,表中数据为速度传感器测出的速度(m/s)。

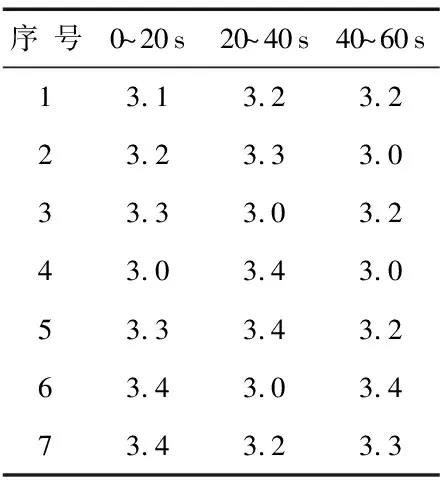
表1 1 min内采样数据

3.3 置信区间的设置

神经网络训练结束后，另取60组未经优化处理的原始数据用来求取残差值[12]，即由预估值和真实值误差确定置信区间。误差服从均值为零的正态分布。假设新近测量值落入预报区间的概率P=100(1-α),则区间的上下界的表达式为

(5)

其中,t∂/2(n-1)为自由度n-1的t分布P百分位；s为误差的标准差。采用这种预报区间的优势在于区间的宽度只受误差的影响。

4 实验数据模拟

矿用皮带秤采用接触式测速，即皮带带动摩擦轮转动产生电压脉冲信号，再由称重仪表转换为相应的速度值(m/s)。皮带运行时由于秤架振动、皮带抖动或摩擦轮打滑都会造成瞬时速度值的波动。取60组数据进行曲线拟合和异常值剔除测试，如图4所示。

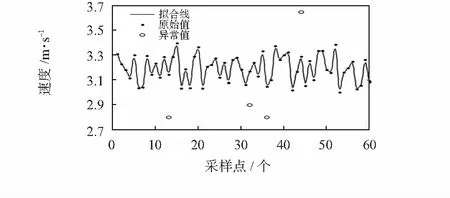
图4 数据检验

由图4可以看出：当皮带速度数据发生抖动产生异常值时，该方法可以有效地剔除异常值。

5 结 论

本文针对速度传感器的延滞性提出了以RBFNN预估为基础，基于历史数据预估下一时刻值的方法，来对速度值进行判定。该方法的优点在于数据驱动对速度传感器模型要求不高，运算量小，适用于实时性较高的场合。经实验检验，95 %的置信区间完全能满足剔除异常数据、保留正常数据的功能。

参考文献:

[1] Hodge V J,Austin J.A survey of outlier detection methodologie-s[J].Artificial Intelligence Review,2004,22:85-126.

[2] Rousseeuw P J,Leroy A M.Robust regression and outlier detection[M].Hoboken:John Wiley & Sons,2005.

[3] Fauconnier C,Haesbroeck G.Outliers detection with the mini-mum covariance determinant estimator in practice[J].Statistical Methodology,2009,6(4):363-379.

[4] Bulut A,Singh A K,Shin P,et al.Real-time nondestructive structural health monitoring using support vector machines and wavelets[C]∥Nondestructive Evaulation for Health Monitoring and Diagnostics,International Society for Optics and Photonics,2005:180-189.

[5] 潘轶彪,袁景淇,朱 凯,等.基于多层感知器的异常数据实时检测方法[J].上海交通大学学报,2011,45(8):1226-1229.

[6] 周桂法,王 坚.基于神经网络的机车速度传感器故障诊断方法研究[J].机车电传动,2010(1):36-38.

[7] 黄治军,雷 勇.传感器故障检测的仿真研究[J].计算机仿真,2005,22(1):110-112.

[8] 许秀玲,汪晓东.传感器故障诊断方法研究[J].佛山科学技术学院学报:自然科学版,2004,22(3):18-22.

[9] 陈 明.Matlab神经网络原理与实例精解[M].北京：清华出版社，2013：196-242.

[10] 李 萍,曾令可,税安泽,等.基于Matlab的BP神经网络预测系统的设计[J].计算机应用与软件,2008,25(4):149-150.

[11] 张秀玲,张志强.四种确定RBFNN中心的新算法[J].工业仪表与自动化装置,2007(2):6-9.

[12] 陆 南,孙茜茜.基于遗传粒子滤波器的传感器故障诊断[J].现代电子技术,2013,36(18):16-19.