功率放大器及预失真器模型的设计

王 伟，曹 民，朱娟娟，王 戈，李 龙

0 引言

随着移动通信市场的迅速发展，对移动通信技术提出了更高的要求。有限的可用频谱资源遏制了现代通信系统的发展。为了通信事业更好地发展，必须提高频谱利用率。

在通信系统中，功率放大器是造成系统非线性的主要来源。当发射信号的功率增加到一定程度时，会使信号进入非线性区域，从而造成频谱拓宽、带内频谱失真。因此，功率放大器的线性化可以抑制频谱泄露、邻道干扰以及减小误比特率［1］。

为了克服上述缺点，在所有线性化技术中，数字预失真技术是补偿功率放大器最有效、最有前景的功放线性化技术之一。

1 数学模型

幂级数模型和多项式模型被广泛用于描述功率放大器的非线性效应。文中主要介绍正交多项式模型。根据函数逼近Weierstrass定理［2］，可以用一个阶数充分大的多项式去逼近功放到任意程度，故可采用正交多项式表示功放的非线性函数。

1． 1 建模原理

信号的功率放大是通信系统的关键功能之一，其实现模块称为功率放大器。功放的基本原理是:输入信号通过功率放大器输出较大功率的信号。预失真器的基本原理是:在功放前设置一个补偿器，它具有功放的逆特征，用来弥补功放的非线性。这两个模块的合成效果使得整体输入－输出特性线性化，输出功率得到充分利用。系统原理如图1所示。

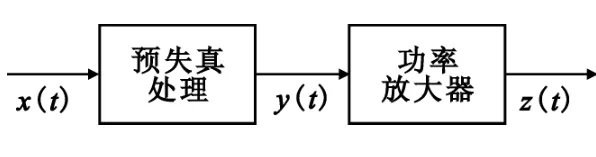
图1 系统原理Fig．1 Principle diagram of the system

设功放输入－输出传输特性为G()，预失真器特性为F()，系统处理原理可表示为:

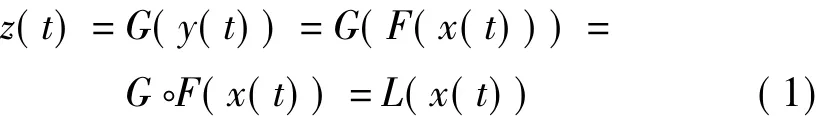
G◦F=L表示为G()和 F()的复合函数等于L()。线性化则要求:

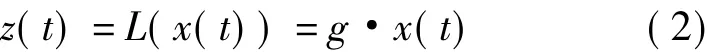
式中，常数g是功放的理想“幅度放大倍数。因此，当功放特性G()已知，则预失真技术的核心是寻找预失真器的特性F()，使得它们复合后能满足:

如果测得功放的输入和输出信号值，就能拟合功放的特性函数G()，然后利用式(3)，可以求得F()。

1． 2 传统多项式模型

在实际运算中，功放输入y(t)、输出z(t)，进行离散采样后值为分别为y(n)、z(n)(采样过程符合Nyquist采样定理要求)，功放模型分为无记忆和有记忆模型两种。传统多项式表示为:

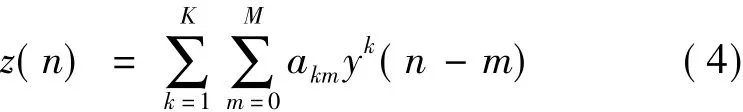
由于常用复值输入－输出信号，式(4)可化为“和记忆多项式”模型:

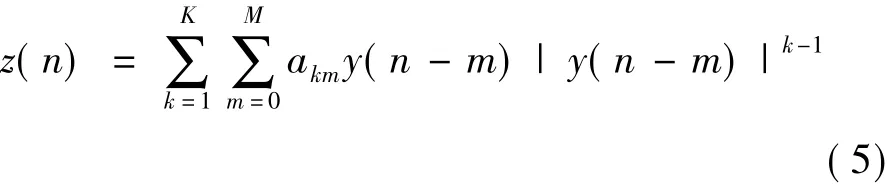
式中，M表示记忆深度，当M等于0时，该形式化简为无记忆功放模型，M不等于0时，该式展开为有记忆功放模型，n 的范围为 n=0，1，2，…，N，akm为功率放大器模型的参数。

预失真器的模型仍为正交多项式模型，其模型为式(5)。

当线性化系统的输出为z(n)时，则系统输入为z(n)/g，即预失真器的输入，而功放的输入为x(n)，即预失真器的输出。所以将预失真器的输入为z(n)/g，输出为x(n)，代入式(5)可得到预失真器的模型:

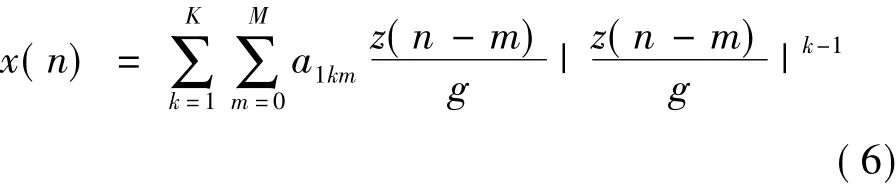
式中，a1km为预失真器模型的参数，g是功放的理想幅度放大倍数。

将原始数据x(n)带入预失真器模型式(5)，输出得到y1(n)，再将y1(n)带入功放模型式(6)中，输出得到z1(n)。

1． 3 正交多项式模型

功放模型用正交多项式可表示为:

用线性最小二乘法求系数矩阵h:

对于无记忆正交多项式:

h表示

φ表示

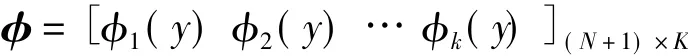
φk(y)表示

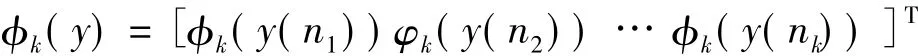
φk(y(n))表示

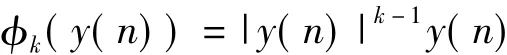
对于有记忆正交多项式［3］:

h表示

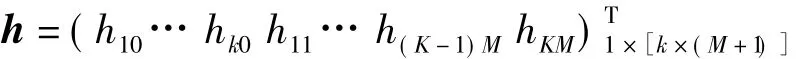
φ表示

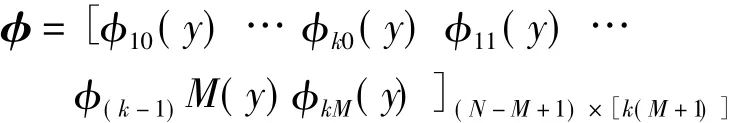
φkm(y)表示

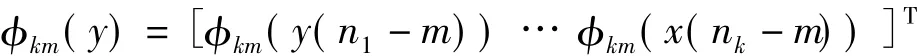
φkm(x(n－m))表示

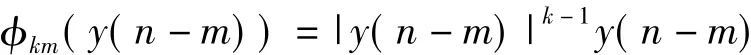
求解步骤同上:先求出功放的系数矩阵，再求出预失真器的系数矩阵。将原始数据x(n)带入预失真器模型，输出得到y2(n)，在将y2(n)带入功放模型中，输出得到z2(n)。

1． 4 评价模型指标

以上模型的数值计算结果常用NMSE和EVM评价整体模型，如下:

采用归一化均方误差 (NMSE)来表征计算精度，如果用z表示实际信号值，˜z表示通过模型计算的信号值，NMSE就反映了模型与物理实际模块的接近程度。

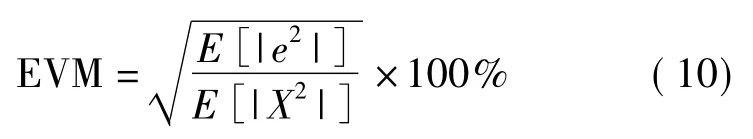
误差矢量幅度(EVM)定义为误差矢量信号平均功率的均方根和参照信号平均功率的均方根的比值。如果用x表示理想的信号输出值，e表示理想输出与整体模型输出信号的误差，那么EVM衡量整体模型对信号的幅度失真程度。

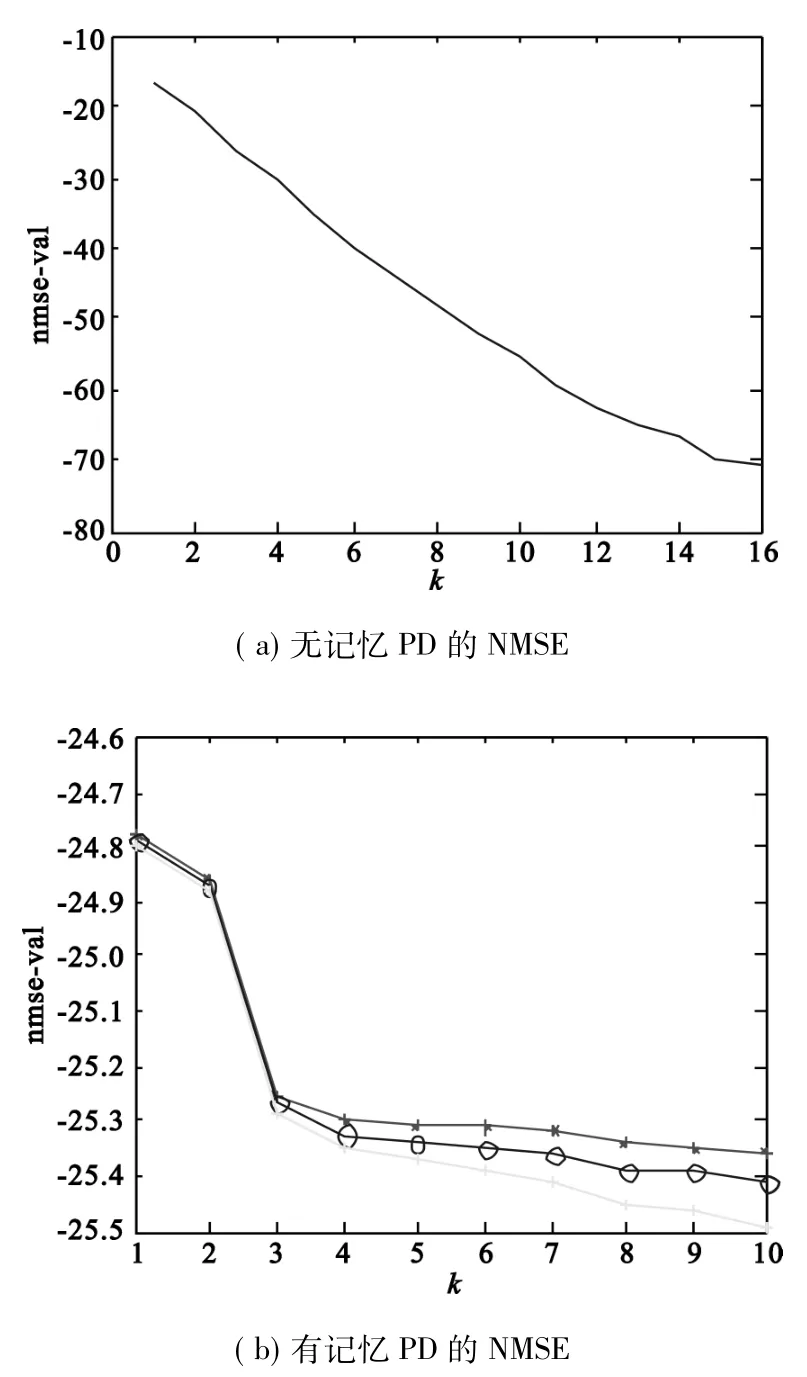
图3 无记忆和有记忆预失真模型的评价指标Fig．3 Evaluation index figure of predistorter models with memory and without memory

2 模型求解

2． 1 正交多项式模型评价指标

系统分为无记忆模型和有记忆模型，评价结果如图2和图3所示。

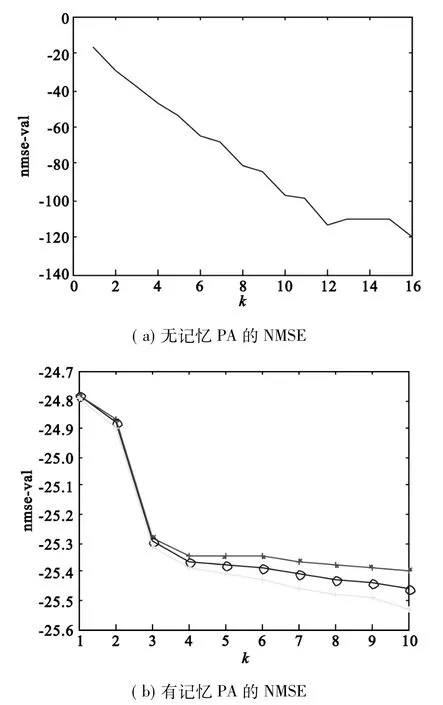
图2 无记忆和有记忆功放模型的评价指标Fig．2 Evaluation index figure of the power amplifier models with memory and without memory

图2 (a)、图3(a)分别为无记忆功放模型以及预失真模型的NMSE图，可知道，无记忆模型的阶数由0递增到16的过程中，NMSE的取值随着阶数的提高迅速降低，客观的反映了正交多项式的阶数在无记忆模型与物理实际模块之间的逼近程度。图2(b)、图3(b)分别为有记忆功放模型以及预失真模型的NMSE图，可知道，有记忆模型的阶数由0递增到10过程中，NMSE的取值随着阶数的提高迅速降低，且记忆深度由1递增到3的过程中，NMSE的取值也会降低，客观的反映了正交多项式的阶数和记忆深度在有记忆模型与物理实际模块之间的逼近程度。

2． 2 正交多项式仿真结果

系统分为无记忆模型和有记忆模型，仿真结果如图4和图5所示。

图4为阶次K=5经过预失真器的无记忆功放模型仿真图，EVM=1．4%;图5为阶次 K=5、记忆深度M=2经过预失真器的有记忆功放模型仿真图，EVM=0．55%，可知道，经过前置预失真器的功放模型，使得整体输入、输出特性满足线性化关系;客观的衡量无记忆和有记忆模型对信号的幅度失真程度。

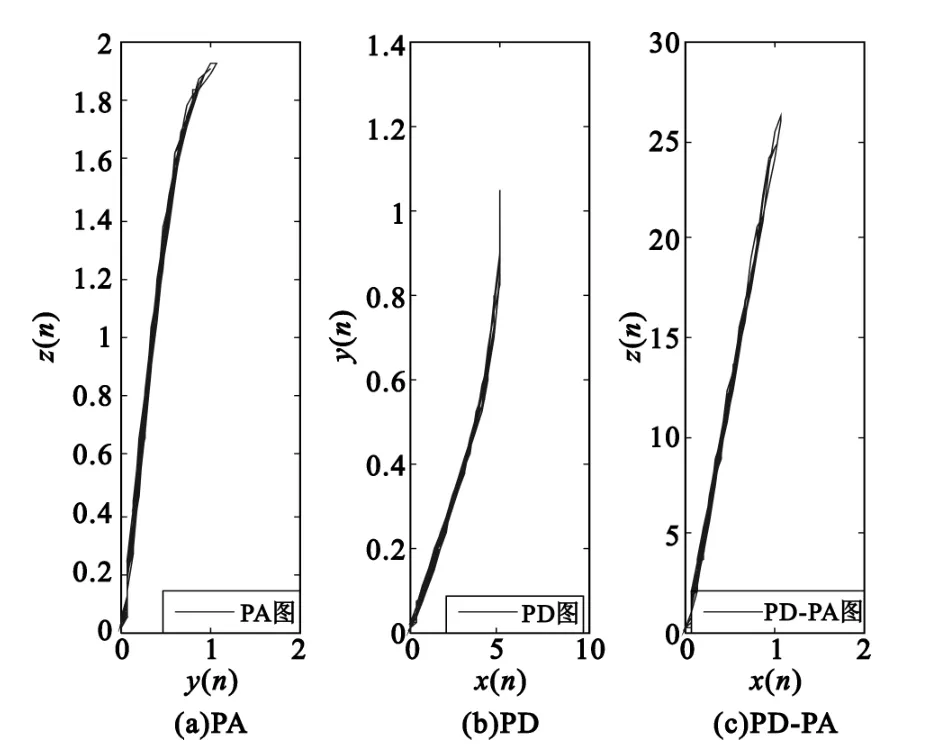
图4 无记忆模型Fig．4 Models without memory

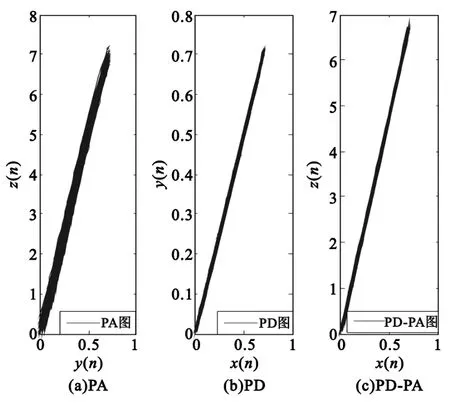
图5 有记忆模型Fig．5 Models with memory

2． 3 正交多项式模型的特点

传统多项式从原理考虑n取越大越好，但由于数据量的限制，MATLAB软件调用polyfit函数无法求出所需高阶多项式的全部参数，且高阶时会引起数值的不稳定;文中引用了正交多项式模型，该方法在求取高阶多项式参数时不受样本数据量的限制，减轻了数值不稳定的问题，建立高精度的功率放大器和预失真器模型，进而改善系统的指标。

3 结语

文中针对无记忆功放和有记忆功放分别建立了预失真模型，其中利用功放的实际输入输出样本数据求取预失真器模型的方法较为巧妙，并最终采用误差矢量幅度对所建模型进行了评价，结果表明，文中所建立的模型的输出值与理想输出值有较好的近似程度，且对信号的幅度有一定程度的改善。

［1］ 胡莉莉，艾渤．功率放大器记忆效应分析及有记忆预失真技术［J］．通信技术，2011，44(05):45 －77．

HU Li－ li，AI Bo．Memory Effect Analysis of Power Amplifier and Predistorter Technology［J］．Communications Technology，2011，44(05):45－77．

［2］ RAVIV R，QIAN Hua，ZHOU Tong．Orthogonal Polynomials for Power Amplifier Modeling and Predistorter Design［J］．IEEE Trans．Vehicular Technology，2004，53(05):1468－1479．

［3］ ZHOU G T，KENNEY J S．Predicting Spectral Regrowth of Nonlinearpower Amplifiers［J］．IEEE Trans．，2002(50):718－722．