改进二进制人工蜂群算法求解多维背包问题

王志刚，夏慧明

（南京师范大学泰州学院数学科学与应用学院，江苏泰州 225300）

改进二进制人工蜂群算法求解多维背包问题

王志刚，夏慧明

（南京师范大学泰州学院数学科学与应用学院，江苏泰州 225300）

针对二进制人工蜂群算法收敛速度慢、易陷入局部最优的缺点，提出一种改进的二进制人工蜂群算法。新算法对人工蜂群算法中的邻域搜索公式进行了重新设计，并通过Bayes公式来决定食物源的取值概率。将改进后的算法应用于求解多维背包问题，在求解过程中利用贪婪算法对进化过程中的不可行解进行修复，对背包资源利用不足的可行解进行修正。通过对典型多维背包问题的仿真实验，表明了本文算法在解决多维背包问题上的可行性和有效性。

人工蜂群算法；多维背包问题；贪婪算法；组合优化

1 前言

人工蜂群[1～4](artificial bee colony，ABC)算法是由Karaboga于2005年提出的一种基于群体智能的仿生优化算法。实验表明，ABC算法比遗传算法(GA)、差分进化算法(DE)、粒子群优化算法(PSO)具有更好的优化性能。由于其具有收敛速度快、控制参数少、易于实现等优点，已引起越来越多的学者关注，并在很多优化问题中取得了成功的应用[5～9]。传统的ABC算法主要用于求解连续空间的优化问题，对于一些采用二进制编码的0～1整数规划问题却难以处理，这已成为限制其发展的一个瓶颈。为此，Marinakis等在2009年提出了一种二进制人工蜂群(binary artificial bee colony，BABC)算法[10]，然而其邻域搜索方式存在一些不足：a.邻域搜索方式是随机的，导致算法的开采能力较弱，收敛速度较慢；b.邻域搜索公式是单维的，使得候选食物源与原食物源极易相同，导致邻域搜索失败，影响算法性能。Pampará等[11]又提出了3种BABC算法，重点在于连续域到离散域的映射，但未研究新的邻域搜索方式。

在前人研究的基础上，本文提出一种改进的二进制人工蜂群(modified binary artificial bee colony，MBABC)算法，并将其应用于多维背包问题的求解。MBABC算法对ABC算法中引领蜂和跟随蜂的邻域搜索公式进行重新定义，并利用Bayes公式决定蜜蜂食物源的取值概率。在求解多维背包问题时，加入了贪婪算法这个有效的局部搜索方法，利用启发式信息，加快算法的收敛速度。通过对多维背包问题标准测试库的仿真实验和与其他算法的比较，表明了本文算法在迭代相同次数的情况下更容易找到最优解，体现了算法的可行性和高效性，为多维背包问题的求解提供了一种新的解决办法，拓展了ABC算法的应用领域。

2 人工蜂群算法

2.1 传统人工蜂群算法

ABC算法主要模拟蜜蜂种群的智能采蜜行为。蜂群主要由引领蜂(employed bees)、跟随蜂(onlookers)和侦察蜂(scouts)三个部分组成。人工蜂群算法在求解优化问题时，食物源代表优化问题的一个可能解，蜂群采蜜(食物源)的过程也就是搜寻优化问题最优解的过程。食物源的优劣取决于优化问题的适应值(函数值)，适应值高的食物源较优。人工蜂群算法中解的个数(SN)等于引领蜂或跟随蜂的个数。用xi=(xi1，xi2，…，xiD)表示第i个食物源(i=1，2，…，SN，D为搜索空间的维数)。首先，人工蜂群算法随机产生SN个解(食物源)，然后蜂群对所有的食物源进行循环搜索，循环次数为MCN。引领蜂首先在食物源的邻域生成一个候选食物源，并比较候选食物源与先前食物源的优劣，如果候选食物源的适应值优于先前食物源的适应值，则用候选食物源代替先前的食物源，否则保持先前的食物源不变。结束之后，引领蜂回到舞蹈区把食物源优劣的信息通过跳摇摆舞传达给跟随蜂，跟随蜂根据所得到的信息按照一定概率选择食物源，适应值越高的食物源被选择的概率越大。跟随蜂选中食物源后，也在食物源的邻域生成一个候选食物源，并比较候选食物源与选中食物源的优劣，保留较优的食物源。人工蜂群算法就是通过上述反复循环来最终找到最优解的。当某个蜜蜂个体经过limit次循环食物源没有更新时，个体放弃该食物源变成侦察蜂，寻找新的食物源。

引领蜂和跟随蜂根据式（1）在食物源的邻域生成一个候选食物源

式（1）中，vij是生成的候选食物源；k∈{1，2，…，SN}，j∈{1，2，…，D}，这两个数都是随机选取的，但k≠i；rij是[-1，1]上均匀分布的随机数，它控制xij邻域的生成范围。随着迭代次数的增加，(xij-xkj)之间的距离缩小，搜索的空间也缩小，即搜索的步长缩小，动态地调整步长，有助于算法提高精度，并最终获得最优解。式(1)称为ABC算法的邻域搜索公式。

跟随蜂通过如下概率来选择食物源

式（2）中，fiti为第i个食物源的适应值，即食物源的适应值越优，其被选择的概率就越大。在最大化问题中，fiti与优化问题目标函数值 fi的对应关系为

在ABC算法中，某个蜜蜂个体如果连续经过limit次循环之后食物源仍然没有得到更新，个体就要放弃食物源，转变为侦察蜂。侦察蜂通过式（4）产生一个新的食物源

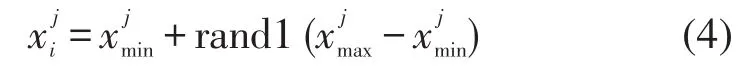
2.2 二进制人工蜂群算法

Marinakis等人提出的BABC算法仿照二进制粒子群优化(BPSO)算法[12]和二进制差分进化(BDE)算法[13]的思想，将初始化得到的xi和邻域搜索公式(1)得到的vi通过logistic函数转换为二进制的和，转换公式为

式（6）、式（8）中，rand2和 rand3均为(0，1)之间均匀分布的随机数。

算法的其他流程与传统的ABC算法相同，在此不再赘述。

3 改进二进制人工蜂群算法

BABC算法继续沿用传统ABC算法中的邻域搜索公式(1)得到的vi转换成二进制的的必要性并不是很强，而且采用的logistic函数的主要功能是限界，并没用充分的理由。此外，在BABC算法中采用单维更新，这使得候选食物源与原食物源极易相同，导致邻域搜索失败。为此，本文对邻域搜索公式进行重新定义。首先，在生成候选食物源vij时，不采取随机选取一个 j∈{1，2，…，D}，而是使j取遍1，2，…，D，这样可以避免候选食物源与原食物源极易相同的缺陷；其次，从式(1)可以看出，vij的取值主要由 xij和 xkj决定，当xij和 xkj取0或1后，可以通过设定xij和xkj判断取0和1的可信度，然后借助Bayes公式来决定vij到底取0还是取1。因此，先作如下两个假定。

1）由于优化过程中vij的真值是未知的，故假定先验概率P(vij=0)=P(vij=1)=0.5。

2）在寻找最优值的过程中，假定xij和xkj对最优值的判定是相互独立的。

记xij作出正确判定的概率为P1，xkj作出正确判定的概率为P2，由Bayes公式可得

式（10）中，p1、p2为xij发现最优值的概率的终值和初始值；iter为当前迭代次数；MCN为最大迭代次数。

4 求解多维背包问题的改进二进制人工蜂群算法

多维背包问题是组合优化领域中一个经典的NP难题，在很多实际工程问题中有着广泛的应用。因而，寻找可以有效解决该问题的算法具有重要的研究意义。目前，许多学者利用不同的思想提出了各种各样的算法来对其进行求解。贺一等[14]借鉴认知心理学有关记忆系统的表述，在禁忌搜索算法中引入长时记忆，构造了基于双禁忌表的禁忌搜索算法，在求解多维背包问题的仿真实验中取得了不错的效果。俞学才等[15]通过定义新的选择概率的规则和基于背包项的一种序的启发式信息，提出了求解多维背包问题的蚁群优化算法。孔民等[16]在蚁群优化系统高维立方体结构的基础上，提出一种二进制蚂蚁算法来求解多维背包问题。冀俊忠等[17]提出基于变异和信息素扩散的多维背包问题的蚁群算法。刘勇等[18]基于元胞自动机的原理和离散粒子群算法，提出一种元胞粒子群算法，该算法具有较好的全局优化能力。除了上述算法外，还有小世界算法[19]、DNA计算[20]、人工鱼群算法[21]等。

多维背包问题可描述为：有n个价值为wj(j=1，2，…，n)的 物 品 ，m 个 容 积 为ci(i=1，2，…，m)的背包，第 j个物品占用第i个背包的体积大小为aij。如何选择物品使其既可以装入这m个背包，又能使装入物品的总价值最大。其数学模型为

式(11)中，f(x1，x2，…xn)为目标函数；n为物品数量；m为背包数量；wj为第 j个物品的价值；ci为第i个背包的体积；aij为第 j个物品占用第i个背包的体积大小；xj为0～1变量，xj=1表示第 j件物品被装入背包，xj=0表示第j件物品没有被装入背包。

采用MBABC算法在求解多维背包问题时通过邻域搜索得到的解不一定可行，为此，引入贪婪算法来修正不可行解，同时在保证解可行的前提下，尽量增加其适应值。若解不可行，则按物品 j的价值密度ρj=cjwj(j=1，2，…，n)由小到大的方向将xj=1变为xj=0，直到将不可行的解变成可行解；若解可行，则在保证解可行的前提下，按ρj由大到小的方向将xj=0变成xj=1，尽量增加其适应值。

求解多维背包问题的MBABC算法步骤如下。

1）设置迭代次数iter，群体规模SN，限定的循环次数limit，最大迭代次数MCN，xij发现最优值的概率的终值p1和初始值p2。

2）初始化种群X(SN×n)，对X中的每个向量xi（i=1，2，…，SN）用贪婪算法修正并计算适应值。

3）引领蜂按式(9)产生候选食物源，用贪婪算法修正并计算其适应值，如果候选食物源vi的函数值优于原有食物源xi的函数值，则用其替换xi，否则保留xi不变。

4）利用式(2)计算与xi有关的概率值qi。

5）跟随蜂根据qi选择食物源，并按式(9)产生候选食物源，用贪婪算法修正计算其适应值，如果候选食物源vi的函数值优于原有食物源xi的函数值，则用其替换xi，否则保留xi不变。

6）判断是否有要放弃的解，如果存在，则按照式(4)随机产生一个满足约束条件的新解来代替它。

7）记录迄今为止最好的解。

8）判断算法是否满足停止条件，如满足则输出最优结果，否则返回步骤3。

5 仿真实验

为了验证本文算法的性能，采用VC++编程，对文献[18]中的55个标准测试算例进行了仿真实验。限于篇幅，本文仅列出文献[18]和其他算法共同采用的较大规模背包问题的实验结果。表1为本文算法与文献[12]的BPSO算法和文献[18]的元胞粒子群算法（CPSO）以及文献[10]提出的BABC算法的实验结果对比，BPSO和CPSO的参数设置见文献[18]，BABC算法和本文算法中群体规模均为100(与BPSO和CPSO的群体规模一致)，limit=50，在本文算法中的另外两个参数 p1和 p2分别取值为p1=0.9，p2=0.1。仿真实验时，对每个算例独立运行20次，记录20次实验中获优次数、最优解、最劣解和平均解。

表1 BPSO、CPSO、BABC和MBABC的性能比较Table 1 Comparison results of BPSO，CPSO，BABC and MBABC

续表

从表1的对比数据可以看出，BPSO在很多情况下没有搜索到最优解或者获优次数很少，极易陷入局部最优而停滞不前；BABC凭借人工蜂群算法良好的优化性能，在最终优化结果上相比于BPSO有显著的改善。但由于BABC采用单维更新，这使得候选食物源与原食物源极易相同，容易导致邻域搜索失败，因而其求解效率不是很高。而MBABC克服了BABC容易陷入局部极值的缺陷，能以较快的速度达到全局最优，有较高的全局寻优性能。在对测试算例进行的仿真实验中要优于BABC以及BPSO和CPSO两种优化算法，表明了本文算法在解决多维背包问题上的可行性和有效性。

6 结语

二进制人工蜂群算法具有收敛速度慢、容易陷入局部最优等问题，针对这一不足，本文提出一种改进的二进制人工蜂群算法，并将其与贪婪算法相结合，应用于多维背包问题的求解。仿真实验结果表明，改进后算法的优化性能明显优于二进制人工蜂群算法和其他一些进化算法，为多维背包问题的求解提供了一个新的思路，并拓展了人工蜂群算法的应用范围。

[1]Karaboga D.An idea based on honey bee swarm for numerical optimization[R].Technical Report-TR06，Kayseri：Erciyes University，Engineering Faculty，Computer Engineering Department，2005.

[2]Karaboga D，Basturk B.A powerful and efficient algorithm for numerical function optimization：artificial bee colony(ABC)algorithm[J].Journal of Global Optimization，2007，39(3)：459-471.

[3]Karaboga D，Basturk B.Artificial bee colony(ABC)optimization algorithm for solving constrained optimization[J].Foundations of Fuzzy Logic and Soft Computing，2007，4529：789-798.

[4]Karaboga D，Basturk B.On the performance of artificial bee colony(ABC)algorithm[J].Applied Soft Computing，2008，8(1)：687-697.

[5]Karaboga D.A new design method based on artificial bee colony algorithm for digital IIR filters[J].Journal of the Franklin Institute，2009，346(4)：328-348.

[6]Singh A.An artificial bee colony algorithm for the leaf-constrained minimum spanning tree problem[J].Applied Soft Computing，2009，9(2)：625-631.

[7]胡中华，赵 敏.基于人工蜂群算法的机器人路径规划[J].电焊机，2009，39(4)：93-96.

[8]胡中华，赵 敏.基于人工蜂群算法的TSP仿真[J].北京理工大学学报，2009，29(11)：978-982.

[9]孙晓雅，林 焰.改进的人工蜂群算法求解任务指派问题[J].微电子学与计算机，2012，29(1)：23-26.

[10]Marinakis Y，Marinaki M，Matsatsinis N.A hybrid discrete artificial bee colony-GRASP algorithm for clustering[C]//International Conference on Computers Industrial Engineering.Troyes，France：[s.n.]，2009：548-553.

[11]Pampará G，Engelbrecht A P.Binary artificial bee colony optimization[C]//IEEE Symposium on Swarm Intelligence.Paris：IEEE，2011：1-8.

[12]Kennedy J，Eberhart R C.A discrete binary version of the particle swarm algorithm[C]//Proceedings of IEEE Conference on Systems，Man，and Cybernetics.Orlando，1997，5：4104-4108.

[13]Pampará G，Engelbrecht A P，Franken N.Binary differential evolution[C]//IEEE Congress on Evolutionary Computation.Vancouver：IEEE，2006：1873-1879.

[14]贺 一，邱玉辉，刘光远，等.多维背包问题的禁忌搜索求解[J].计算机科学，2006，33(9)：169-172.

[15]喻学才，张田文.多维背包问题的一个蚁群优化算法[J].计算机学报，2008，31(5)：810-819.

[16]孔 民，田 澎，李相勇.多维背包问题的二进制蚂蚁算法[J].管理科学学报，2009，12(2)：44-53.

[17]冀俊忠，黄 振，刘椿年.基于变异和信息素扩散的多维背包问题的蚁群算法[J].计算机研究与发展，2009，46(4)：644-654.

[18]刘 勇，马 良.元胞微粒群算法及其在多维背包问题中的应用[J].管理科学学报，2011，14(1)：86-96.

[19]杜 巍，李树茁，陈煜聪.一种求解多维背包问题的小世界算法[J].西安交通大学学报，2009，43(2)：10-14.

[20]刘 毅，宋玉阶.多维背包问题的DNA计算[J].生物数学学报，2008，23(1)：180-186.

[21]李春梅，马 良.求解多维0-1背包问题的人工鱼群算法[J].数学的实践与认识，2010，40(17)：195-199.

Modified binary artificial bee colony algorithm for multidimensional knapsack problem

Wang Zhigang，Xia Huiming
（School of Mathematics，Nanjing Normal University Taizhou College，Taizhou，Jiangsu 225300，China）

The binary artificial bee colony algorithm has the shortcomings of slower convergence speed and falling into local optimum easily.According to the defects，a modified binary artificial bee colony algorithm is proposed.The algorithm redesign neighborhood search formula in artificial bee colony algorithm，the probability of the food position depends on the Bayes formula.The modified algorithm was used for solving multidimensional knapsack problem.During the evolution process，it used the greedy algorithm to repair the infeasible solution and rectify feasible solution with insufficient use.The simulation results showed the feasibility and effectiveness of the proposed algorithm.

artificial bee colony algorithm；multidimensional knapsack problem；greedy algorithm；combinatorial optimization

TP301.6

A

1009-1742（2014）08-0106-07

2013-11-11

南京师范大学泰州学院资助项目(Q201232)

王志刚，1978年出生，男，山东潍坊市人，讲师，主要研究方向为组合优化与算法研究；E-mail：wzg19.scut@163.com