基于PFGA的步进电机PWM发生器设计
2014-09-22,
,
(1.上海交通大学电子信息与电气工程学院,上海 200235;2.上海航天技术研究院,上海 201108)
1 引言
目前,步进电机普遍采用细分驱动方式,可以有效降低整步或半步驱动带来的速度波动、低频振荡等缺点。本质上,细分驱动是将步进电机的驱动电磁场均匀化,使驱动力矩保持近似恒定。对于常用的两相混合式步进电机,其细分驱动是通过使一相电流按正弦规律变化,而另一相电流按余弦规律变化。常用细分数来衡量电机电流与正弦波的接近程度。一般而言,使用单片机系统加外围基本电路可以实现常规的步进电机细分驱动系统。但由于单片机运算能力有限,且运行频率不高(一般不超过20 MHz),其产生方波的能力不超过40 kHz,而细分数量越高,需要产生方波的频率也越高,所以单片机系统的细分数量比较有限。
随着IC技术的发展,器件运行的频率大大提高,例如采用DSP,FPGA等,比较容易产生1 MHz以上的方波,对于步进电机驱动系统非常适用。
2 步进电机常用细分驱动电路
根据步进电机末端功率管的工作状态,步进电机可以分为放大型驱动和开关型驱动。放大型驱动是功率管工作在电流放大状态,尽管放大型驱动电路可以获得比较好的细分,但功率管在此状态下效率较低,有效输出少,所以放大型驱动电路一般用在小功率、驱动精度高的场合。由于功率管中需要放大正弦曲线的电流,所以放大型驱动电路需要DAC(数字-模拟转换器)实现。开关型驱动电路又可以分为斩波型和PWM型。斩波型驱动电路,是利用电机真实绕组电流的反馈值与设定值(正弦曲线,每个设定点一般为一个阈值区间)进行比较,小于设定值下限时,开关管打开,绕组电流上升,大于设定值上限时,开关管关闭,绕组电流下降。斩波型驱动电路需要电流反馈值和设定值进行比较,根据比较器的类型,可以分为模拟比较器和数字比较器。模拟比较器使用DAC(数字-模拟转换器)将设定值转化为模拟电压值实现[1],数字比较器采用ADC(模拟数字转换器)将电机绕组真实电流转化为反馈数字量[2],在数字系统中进行比较。斩波型驱动电路如图1、图2所示。

图1 模拟比较式斩波电路Fig.1 The analog chopping circuit
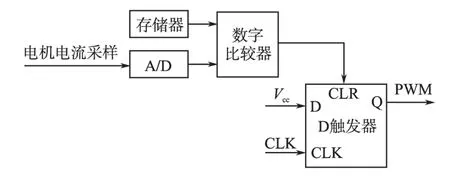
图2 数字比较式斩波电路Fig.2 The digital chopping circuit
上述斩波型驱动电路已获广泛应用,但由于此电路需要ADC或DAC,额外增加了系统的成本。
PWM(脉冲宽度调制)技术目前广泛应用于电机驱动、电源等系统中。通常PWM信号在数字系统中通过构造随系统时钟递增/递减的数据模拟锯齿波(载波)信号,通过计算或查表方式得到正弦波(调制波)信号,二者比较控制输出为0/1(即占空比数据)。常见的PWM系统[3]如图3所示。
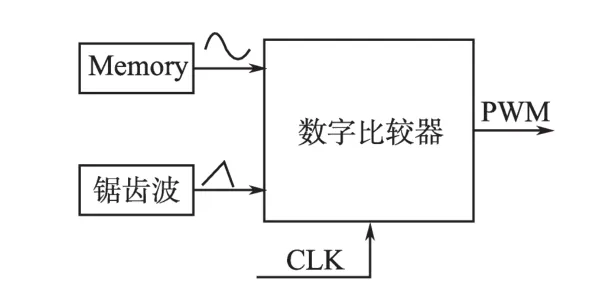
图3 PWM步进电机驱动电路Fig.3 The stepper motor driving circuit using PWM
3 PWM占空比序列
3.1 占空比推导
在采样定理中,有一个重要理论,即形状不同而冲量相等(即面积相同)的任意窄脉冲,通过惯性环节的效果基本相同。基于此理论,可以将正弦波信号转换为占空比不同的周期方波信号(即脉冲宽度一直在调整变化的信号,PWM)。对于方波信号,由于只存在两种状态(高电平和低电平),PWM非常适于二进制系统。工程中针对正弦波的脉宽调制为:采用锯齿波为载波,正弦波为调制波,利用数字或模拟比较器对载波和调制波进行比较,输出为占空比不同的方波。从PWM实现上看,占空比是PWM控制方式的重要数据,PWM输出的方波频率与载波频率一致,电机绕组两端的电压完全由占空比数据决定,从而控制了电机电流。下面对占空比进行计算说明。
假定对归一化正弦波用归一化的锯齿波进行调制,推导占空比计算如下:

式(1)表示电机中电流绕组。由于正弦波的对称性,现对1/4周期的正弦波(即电机绕组电流从0变化到最大)进行分析。对于余弦波,与正弦波相位差90°,即电流从最大变化到最小,数据反顺序即可实现。假定T表示1/4周期正弦波时间,则

假定在T时间内的正弦波被细分成N份(1≤N,N为正整数),则每份的时间为
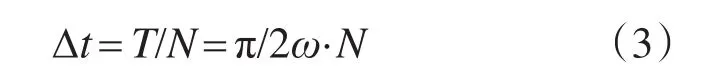
对于其中第k份(1≤k≤N),其所在时间为[(k-1)·Δt,k·Δt],由式(1),其冲量(即面积)为
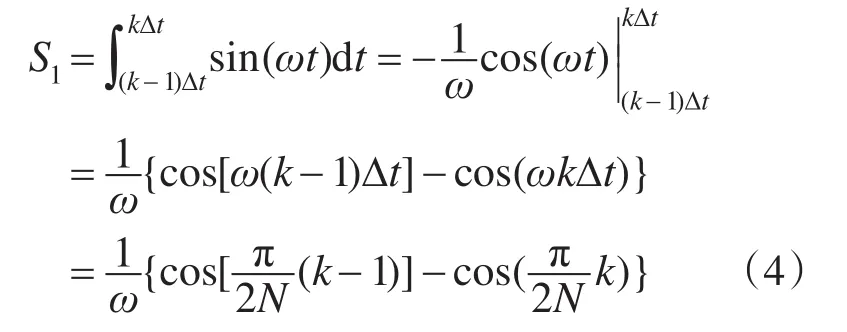
假定调制后的方波占空比为Duty_cycle_k,则
方波的面积为
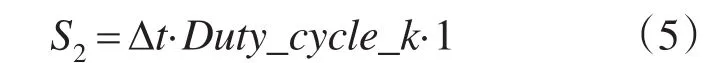
根据二者面积相等,由式(3)~式(5)得出:
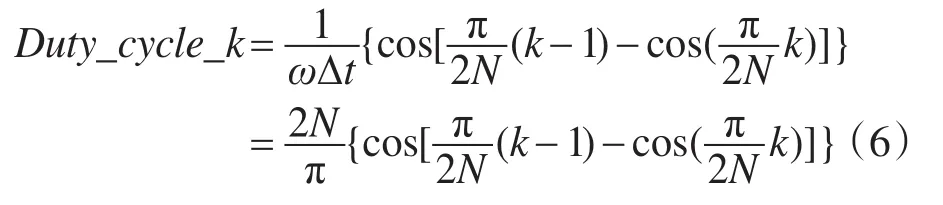
用Δθ表示当Δθ趋于无穷小时,式(6)可以表示为
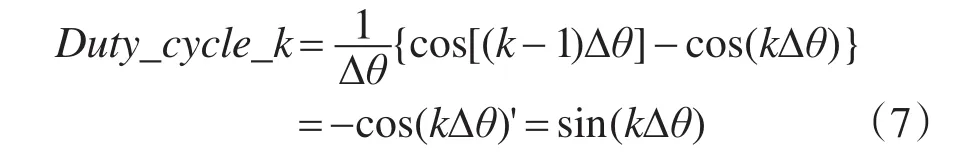
根据上述推导公式(6),可以得出如下结论:对于任意正弦波信号细分成N份,每份的占空比可以直接计算得出(从而形成PWM占空比序列);对于归一化正弦波而言,占空比数据只和细分数量有关;若载波和调制波保持恒定的频率关系时,即细分数量保持不变时,占空比数据保持不变。
由式(7),可以得出如下结论:当细分的数量足够多,占空比数据可以采用简化计算方法,计算某个相位上的正弦值即可。
3.2 占空比整数化
上述计算出的占空比为0~1之间的小数,在二进制数字系统中特别是FPGA系统中,处理的数据直接影响系统的运行速度。而采用整数类型的数据,可以保证系统高速处理。因此对于上述数据的二进制格式化采用了如下方式进行。
对于调制成N份的调制信号,占空比的最大分辨率应不大于1/N。因为,对于整数类型数据处理的数字系统而言,如果分辨率大于1/N,若相邻周期的占空比为k/N,(k+1)/N,则此数字系统无法分辨,也无法执行,增大了电流误差。当然,分辨率可以进一步提高,但导致数字系统的运行频率会相应提高,系统资源开销增大。
因此,基于上述分析,工程化PWM调制系统中,采用了N份调制、1/N占空比分辨率设计,则调制信号(fs)、载波信号(fc)、数字系统的频率(fd,直接产生PWM调制方波)之间的关系如图4所示。
图4中,以其中第2份为例,假定圆整后(存在截位误差)的占空比为2/N,则将第2份进行N等份细分,其中两份为高电平1,其余为低电平0,则第2份的占空比为2/N。对于其它的占空比,如k/N(1≤k≤N),以此类推。理论上高电平的位置任意,不影响实际效果,但在不同的相邻方波中,位置应保持相对固定,以降低电机绕组中电流波动范围。

图4 占空比量化示意图Fig.4 Transforming the duty-cycles to the integers
基于以上分析,调制信号(fs)、载波信号(fc)、数字频率(fd)的关系为
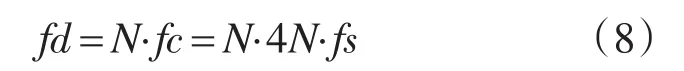
占空比整数化的方式为
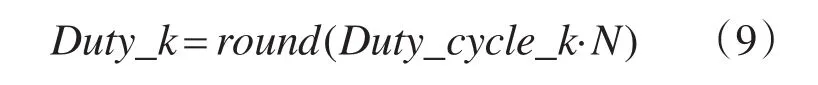
3.3 结果比较
根据以上分析,按正弦波256细分,在Matlab/Simulink中对PWM进行了仿真,采用单方向同极性调制方式。仿真模型和结果如图5所示。

图5 仿真模型及结果Fig.5 The simulation model and results
图5b仿真结果中,调制波与载波比较(曲线1为调制波,标准正弦波;曲线2为三角波),得到占空比数据序列(曲线3),利用此序列控制电机驱动电路,得到电机绕组中实际电流曲线(曲线4)。根据式(6)、式(7)、式(9)分别计算了256细分情况下理论占空比、简化占空比、整数化占空比。结合仿真结果,将上述占空比数据进行了比对,具体如表1所示。

表1 占空比数据比较(部分数据)Tab.1 The result of different duty-cycles(partial)
上述占空比数据的主要误差为整数化截尾误差,最大误差为±0.5/N(四舍五入)。可以看出:采用锯齿波与正弦波比较所得整数化占空比与理论计算非常一致,证明了理论分析的正确性;而由于细分数量不够大,采用简化计算整数化的占空比误差稍大。
4 PWM发生器设计
根据上述PWM占空比计算,得到PWM占空比序列。将此占空比序列实现后,在电机驱动时,即可实现电机绕组中电流按正弦波规律变化。PWM发生器采用Altera公司EP2C5系列FPGA作为主控芯片[5],采用DDS方式实现多种频率的方波信号,即式(8)中的fd,从而实现步进电机的任意细分。FPGA系统框图如图6所示。

图6 FPGA系统框图Fig.6 The system description of FPGA
其中,产生任意频率的DDS模块向PWM发生模块提供根据式(8)计算出的时钟信号。晶振时钟与数字时钟的关系如下:

DDS原理在此不详述,根据式(10),合理地选择M(任意数,通过改变频率控制字实现)、N(正整数,细分数量),实现电机驱动电流的任意细分数量,同时需要同步更新占空比脉冲序列数据。FPGA中DDS合成电路如图7所示[5]。
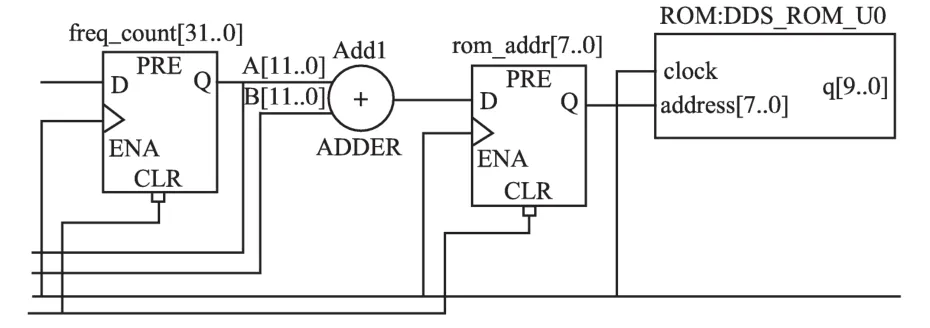
图7 DDS电路图Fig.7 The schematic of DDS
实际系统中采用50 MHz时钟晶振,利用DDS可以产生0~20 MHz之间的任意频率方波(与计数器位数有关,采用32位计数器时,频率分辨率为0.012 Hz),对于单步256细分情况,DDS方式下电机最高工作频率为76 Hz;直接采用100 MHz的标准时钟下,电机最高工作频率为190 Hz。改变细分数量或调整晶振频率可以扩展电机工作频率。
5 结论
提出了一种采用直接占空比序列产生步进电机细分驱动的计算方法。对此算法进行了推导,得出了占空比序列计算公式和简化计算公式,并对占空比数据进行了二进制整数化处理。与Matlab中的仿真结果进行比对,二者一致性好。利用DDS产生任意频率的方波,作为PWM发生模块的时钟,结合直接占空比序列可以实现步进电机的任意数量细分驱动。
[1]Weerakoon T S,Samaranayake L.Development of a Novel Drive Topology for a Five Phase Stepper Motor[C]//IEEE Region 10 and the Third International Conference on Industrial and Information Systems(ICIIS),2008.
[2]荣盘祥,张亚慧,张欢欢,等.基于DSP的运动控制卡的研究与开发[J].电机与控制学报,2011,15(3):35-39.
[3]吴云,陆锷,赵海洋,等.基于FPGA的步进电机细分驱动器的设计[J].自动化仪表,2009,30(10):61-63.
[4]潘明,许勇.基于FPGA的直流电机脉宽调制控制[J].广西科学院学报,2005,21(4):219-221.
[5]马泽龙,唐小琦,宋宝,等.编码器正余弦信号跟踪环路细分技术研究[J].电气传动,2012,42(5):50-52.
