圆曲线拟合方法及数据采集分析

潘桂新，邓德标

(1.中山市黄圃测绘工程有限公司，广东中山 528429;2.广东南方数码科技有限公司，广东广州 510665)

1 引言

测量工作中有时会遇到对几何物体进行检测，如呈直线物体分布形状，只要采集两个点的平面坐标就能根据直线方程反算方程系数;又如空间平面物体，在物体表面采集3个不共线的点，根据三维坐标即可求出空间平面方程。

由于制造工艺和测量误差的原因，物体往往不是严格的几何形状，而根据有限的测量数据也不能严密地反算出物体设计时的几何方程，所以实际工作中会进行多余观测，通过一定数量的数据去拟合物体的几何方程，如直线拟合［1，2］、平面拟合［3，4］、二次曲面拟合［5］和球面拟合［6］。本文研究水平面上的圆曲线拟合方法，根据圆曲线的参数方程推导出相应的误差方程，通过平差计算求出圆心坐标和半径，并通过模拟分析得出一些对圆状物体进行测量的实用结论。

2 圆曲线拟合模型

拟合模型是测量平差中常遇到的一种特殊的函数模型，是一种函数逼近型或统计回归型模型。在圆曲线或圆柱上采集若干个点(如图1所示)作为独立观测量，根据圆曲线方程可求出圆心坐标及圆半径，由于采集点有误差，各个点并不在圆周上，要在这些采集点上拟合出一条最佳圆曲线。

在半径未知的情况下，设采集点个数为m，以圆心的坐标平差值、半径平差值和圆心至各采集点的方位角平差值^αi为参数，圆曲线的参数方程为:

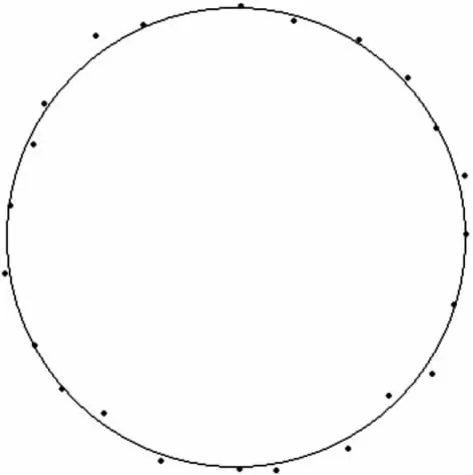
图1 圆曲线拟合

将式(1)线性化，得误差方程为:

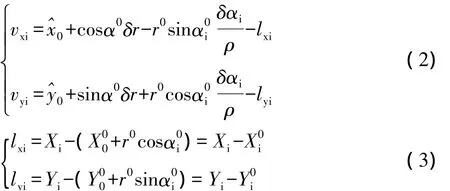
若半径已知，则误差方程如下:

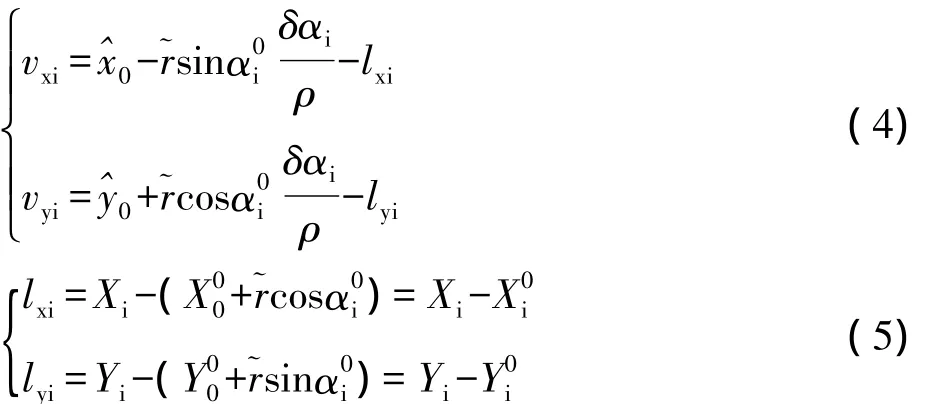
根据间接平差模型:V=B^x－l。令:

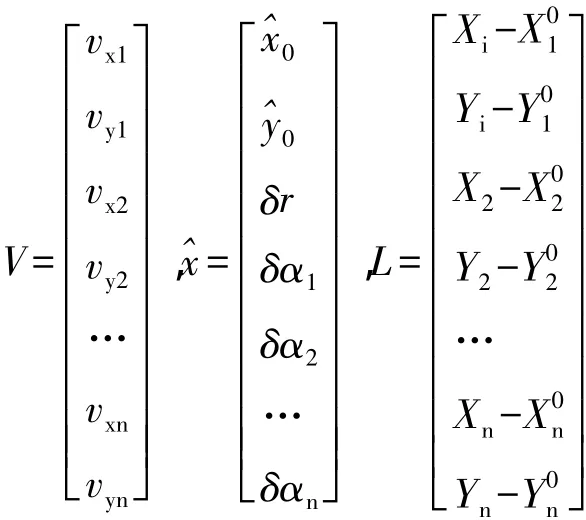
根据式(6)可算得圆心的坐标和半径平差值。

由协因数阵Q=(ATA)－1和验后单位权中误差可得参数的协方差阵，其中n为误差方程总数，t为参数个数，由此可计算误差方程中各参数的中误差进行精度评定。

3 数据处理分析

在实际测量和计算中，由于测量误差、数据采集的位置、采集的数据量及半径是否已知等情况的不同，直接影响到计算结果的正确性，故下面分别针对这4种情况进行模拟分析。

在AutoCAD上绘制一个半径为 1 m的圆，其圆心坐标为(1456.299，337.005)，使用“定数分段”功能在圆周上生成一定数量的节点，再利用捕捉功能采集各个节点坐标作为基础数据，最后利用MATLAB软件中的random函数生成服从标准正态分布的随机数，作为观测误差添加到基础数据中来模仿实际测量的采集数据。

3.1 采集点精度分析

根据误差传播定律可知，采集点的精度会影响到拟合后的圆心坐标精度，现在模拟5组对同个圆均匀采集 20个点的数据，分别附加 ±5 mm、±10 mm、±15 mm、±20 mm、±30 mm的误差，分析不同精度的采集点会对拟合结果产生多大的影响，圆柱半径作为未知数，结果如表1和图2所示。

不同精度的采集点解算结果 表1

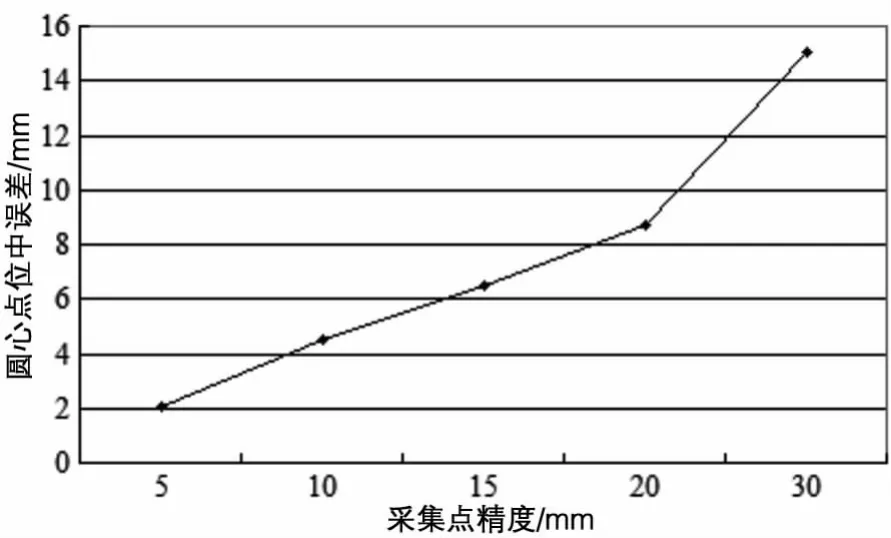
图2 采集精度与圆心点位精度的关系

3.2 采集点数量分析

为分析采集点的数量对拟合后圆心点位中误差的影响，现在圆上均匀地采集 5、10、15、20、30 个点，采集点均随机附加 ±15 mm的误差，半径未知，解算结果如表2和图3所示。

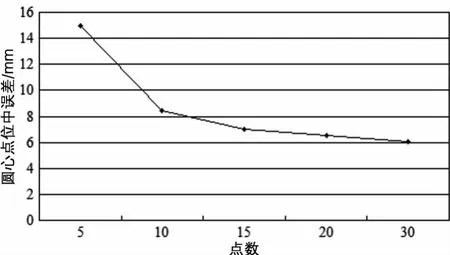
图3 采集点个数对应的对拟合精度

采集点数不同解算结果 表2

3.3 采集点位置分析

在对圆状物体进行观测的工作中，往往因其他物体的遮挡或设站点的位置使得不能够对圆柱进行全方位地采集数据。为分析在不同范围内的采集数据对拟合结果的影响，下面分别对1/4圆、2/4圆、3/4圆、4/4圆这4种范围进行分析，各个范围均采集15个点，采集点精度约为 ±15 mm，以半径未知的形式进行拟合计算，结果如表3和图4所示。

不同采集范围的对比结果 表3

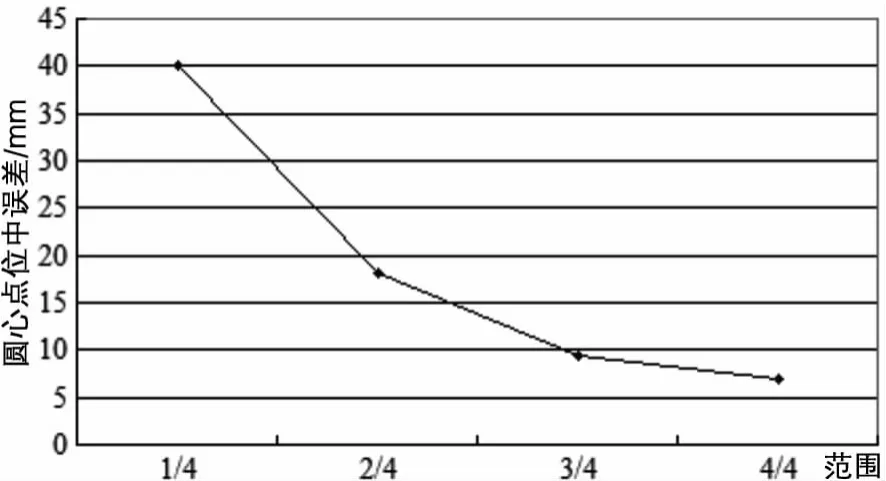
图4 不同的采集范围对拟合精度的影响

3.4 半径已知分析

以上分析都将半径作为未知量根据式(2)进行求解的，下面将半径作为已知量并利用式(4)进行解算，得到的圆心中误差跟前面的结果作对比，分别如图5、图6和图7所示。

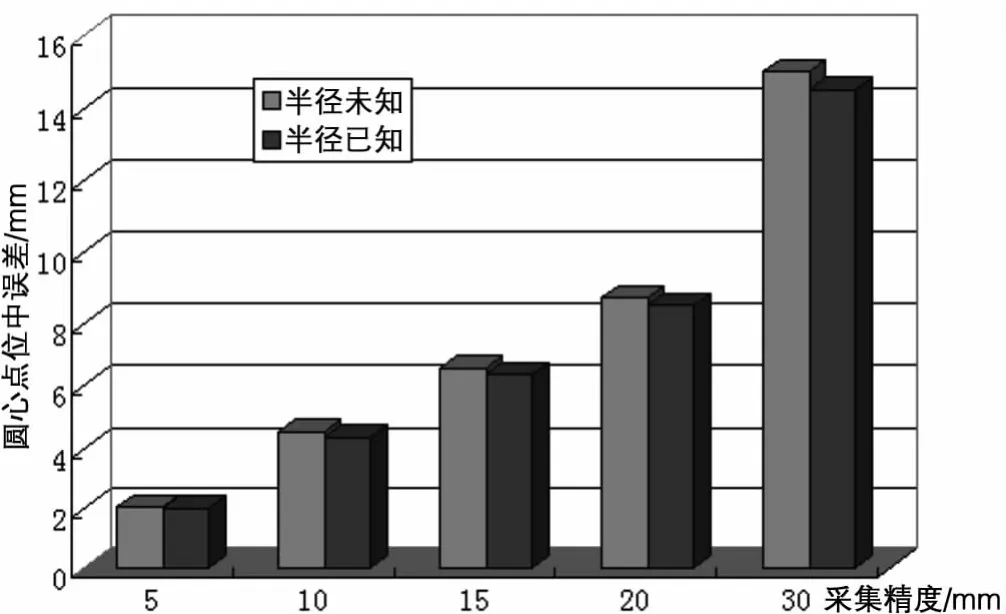
图5 采集精度的影响

图6 拟合点数的影响

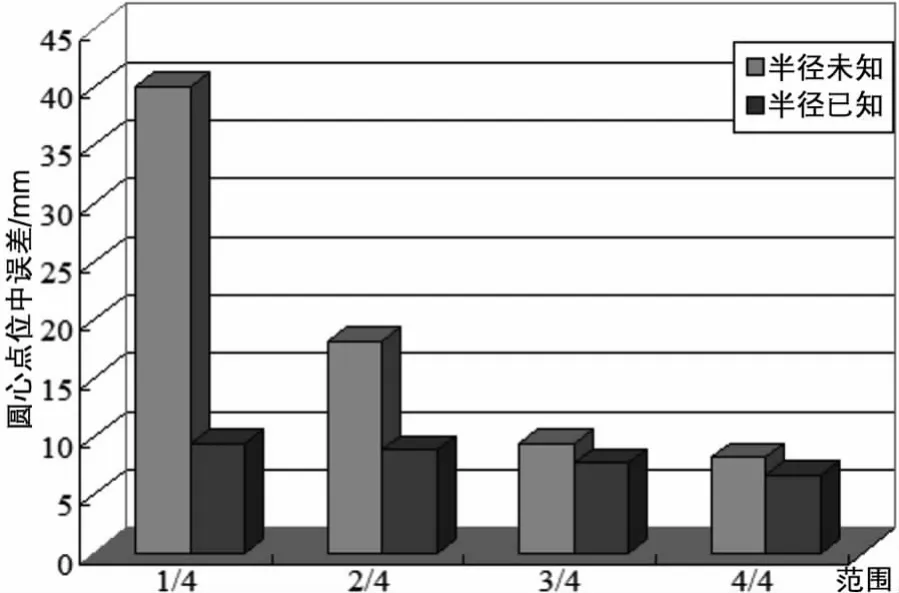
图7 采集范围的影响

4 结语

通过对以上模拟数据的分析，可得出以下4个结论:

(1)由表1和图2可知，在采集点个数和分布情况相同的前提下，观测精度和拟合精度大致呈正相关的线性关系，即观测精度越高，拟合后得到的圆心坐标和半径的精度也越高。

(2)由表2和图3可知，均匀采集的点数越多拟合的精度就越高，但当点数达到一定数量后，精度提高的幅度不明显，建议均匀采集10～15个点比较合适。

(3)由表3和图4可知，采集点的分布对拟合精度有很大的影响，应尽量只在1/4的范围内采集，在半径未知的情况下，采集区域应在圆的3/4以上。

(4)由图5、图6、图7可知，半径已知的解算结果表明拟合精度相对较高，特别是在采集范围较小的情况下能大大提高圆心的点位精度，因此若半径已知可缩小采集范围。

为深入研究，可结合文献［7］和文献［8］所述的粗差探测方法，对拟合数据进行粗差检验，从而提高平差结果的精度和可靠性。

［1］郭际明，向巍，尹洪斌.空间直线拟合的无迭代算法［J］.测绘通报，2011(2):24～25.

［2］丁克良，沈云中，欧吉坤.整体最小二乘法直线拟合［J］.辽宁工程技术大学学报·自然科学版，2010，29(1):44～47.

［3］官云兰，程效军，施贵刚.一种稳健的点云数据平面拟合方法［J］.同济大学学报·自然科学版，2008，36(7):981～984.

［4］程效军，唐剑波.基于最小二乘拟合的墙面平整度检测方法［J］.测绘信息与工程，2007，32(4):19～20.

［5］王解先.工业测量中一种二次曲面的拟合方法［J］.武汉大学学报·信息科学版，2007，32(1):47～50.

［6］邓德标，方源敏，赵子龙等.空间球状物体的数据采集与分析［J］.测绘科学，2013，38(5):146～148.

［7］李华，宗琴，卜立军.基于不同学科解决粗差探测问题的方法研究［J］.测绘科学，2012，37(5):14～16.

［8］关叶沆，周西振，刘传瑞.一段圆弧上多点坐标拟合圆心位置的可靠性分析［J］.勘察科学技术，2012(4):54～57.