模块化多电平变流器调制策略研究

，，，，

（中国矿业大学信息与电气工程学院，江苏徐州 221008）

1 引言

模块化多电平变流器（MMC）由于其众多的优点得到了越来越多的关注［1-2］。文献［1］提出的MMC采用子模块串联的方法，避免了诸如两电平和三电平变流器利用大量开关器件的直接串联来达到高压大功率的目的。

文献［2-3］分析了电压空间矢量调制技术（SVPWM）的调制策略。文献［4］提出了一种改进的PWM调制策略。文献［5］分析了阶梯波调制策略。文献［6-8］分析了载波移相调制策略。

本文针对MMC的拓扑特点，根据MMC各相投入的子模块总数是否恒为N的原则，基于载波层叠技术，研究了其输出相电压为N+1电平和2N+1电平的调制策略，并提出了实现方案，该调制策略无须数学计算就可以得到各桥臂中子模块投入的数量和处于PWM状态的子模块的占空比信息，且电容电压均衡时只进行排序，避免了闭环控制，且易于扩展到任意电平数。最后在Matlab/Simulink仿真环境和搭建的实验平台上，对这两种调制策略进行了仿真分析和实验验证。

2 MMC基本原理

2.1 MMC的拓扑结构

MMC子模块及三相主电路拓扑结构如图1所示，每相分为上、下桥臂，各桥臂由N个子模块组成，上、下桥臂通过桥臂电抗L相串联。各子模块均由一个半桥结构和直流电容C串联组成，各子模块通过端点A和端点B与外部相连。通过对子模块中上、下开关管的控制，可以实现对直流电容的规律性充电与放电。

图1 MMC子模块及三相主电路拓扑结构Fig.1 The topology of three phases MMC and submodules

2.2 工作原理

MMC子模块的工作状态如图2所示，分别为旁路、投入与切除状态，每种状态根据流经子模块的电流方向分为两种工作模式。

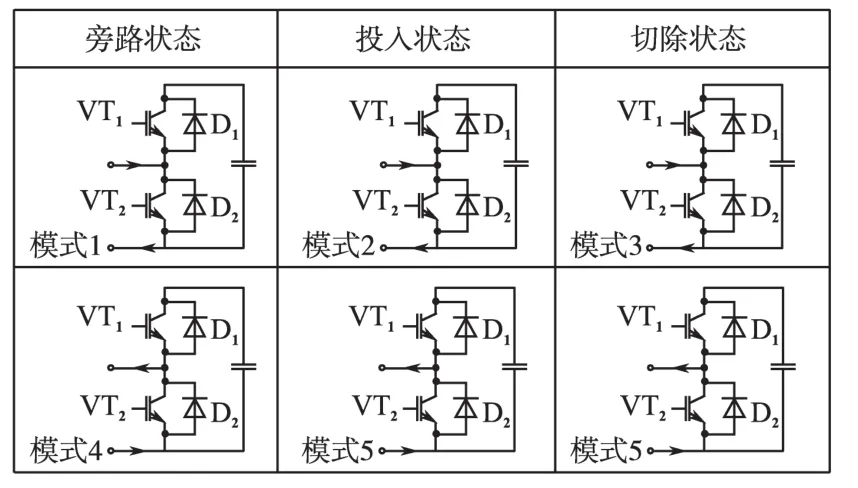
图2MMC子模块工作状态Fig.2 The working condition of the submodules of MMC

根据各相中子模块投入的个数是否恒为N的原则，来实现输出相电压为N+1电平与2N+1电平［4］。以图1中的A相为例，当其满足下式时，输出相电压电平数为N+1电平。

式中：Npa为上桥臂投入的子模块个数；Nna为下桥臂投入的子模块个数。

当其满足下式时，输出相电压电平数可以达到2N+1电平。

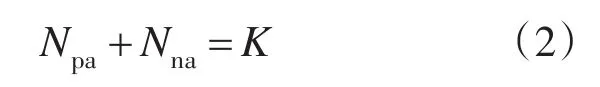
式中：K取值为N-1，N，N+1。

要维持直流侧电压的稳定，需要每相中投入的子模块电压和与桥臂电抗压降之和为直流侧电压。假如各相子模块电容电压完全均衡，并为USM。当该相投入子模块个数满足式（1）时，桥臂电抗压降之和为0，满足式（2）时，桥臂电抗压降之和大小在0，-USM，USM之间变化。MMC的环流分量是由桥臂电抗压降之和的大小决定的［7］，该特性使得输出相电压为2N+1电平时，MMC相间环流相对于输出相电压为N+1电平时较大，会增大MMC系统损耗。而随着输出电压电平数目的增多，在同等开关频率下输出相电压为2N+1电平的THD减小，进而简化输出滤波器的设计，同时其输出电压du/dt减小会减轻其引起的电磁干扰。

3 载波层叠技术

载波层叠技术采用调制波与多个叠加的载波相比较的方式，产生相应的数量触发脉冲，易于MMC扩展任意电平数目。

3.1 载波层叠调制策略

根据三角载波之间相位关系的不同，载波层叠调制分为：同相层叠、正负反向层叠、交替反向层叠调制，本文针对同相载波层叠调制进行分析。同相载波层叠调制策略如图3所示，其中C1，C2，C3，C4为4个相位相同的载波，Us（t）为调制波，在每个载波周期Tc内，调制波和载波相比较，产生4路脉冲，根据电容电压均衡策略，将其分配给相应的子模块控制其工作状态。

图3 同相载波层叠PWM调制Fig.3 Carrier phase disposition PWM modulation

3.2 载波层叠技术实现N+1电平

上桥臂载波与调制波如图3所示，在每个载波周期Tc内，通过调制波与载波的比较可得N路触发脉冲，其中包括Npa路开通脉冲使相应数量的子模块处于投入状态，1路PWM脉冲使1个子模块的工作状态在投入与切除之间变化，N-Npa-1路关断脉冲使相应数量的子模块处于切除状态，将此N路触发脉冲发送给上桥臂的N个子模块作为其开关管的触发信号，同时将此N路脉冲取反，发送给下桥臂的N个子模块作为其开关管的触发信号，则上下桥臂中的PWM脉冲互补。可保证在各个时刻该相上、下桥臂投入的子模块总数恒为N，满足式（1），可实现输出相电压为N+1电平。

3.3 载波层叠技术实现2N+1电平

当上、下桥臂的载波相同，且调制波反向时，在每个载波周期Tc内，通过调制波与载波相比较，上桥臂产生Npa路开通脉冲，1路PWM脉冲，N-Npa-1路关断脉冲，下桥臂产生N-Npa-1路开通脉冲，1路PWM脉冲，Npa路关断脉冲。因上、下桥臂产生的PWM状态的脉冲并不能保持为互补状态，导致在各个时刻一相上、下桥臂中处于投入状态的子模块数量不恒为N。图4以A相为例，在一个载波周期Tc内，分析了该相各时刻投入的子模块总数，因通常载波比很大，可假定调制波的大小在Tc内为一常数，其中上桥臂调制波为Upa_s，下桥臂调制波为Una_s。

图4 载波周期Tc内A相投入的子模块个数Fig.4 The number of inputting submodules of phase A in carrier cycle Tc

由图4可知，在载波周期Tc内，对任意Upa_s与Una_s的取值，A相投入的子模块总数，在t0—t1与t4—t5内为 N+1 个，在 t1—t2与 t3—t4内为 N 个，在t2—t3内为N-1个，满足式（2），则可实现输出相电压为2N+1电平。

3.4 子模块电容电压均衡策略

应用载波层叠技术实现输出相电压为N+1电平与2N+1电平的调制策略所采用的均压策略相同：首先根据采样的子模块电容电压值进行排序，当桥臂电流为正时，处于投入状态的子模块会吸收功率进行充电，将电容电压值较小的子模块投入，使其充电以升高其电压值。当桥臂电流为负时，处于投入状态的子模块会释放功率进行放电，将电容电压值较大的子模块投入，使其放电以降低其电压值。通过控制子模块的充放电，来达到子模块电容电压均衡的目的。调制波与载波的比较结果决定了子模块处于投入与切除状态的数量，子模块电容电压排序结果和桥臂电流方向决定了子模块的工作状态，在硬件条件允许的情况下，该均衡策略并不受桥臂中串联的子模块数量的限制，理论上可实现MMC输出任意电平数。

4 仿真分析

4.1 输出相电压N+1电平仿真分析

在Matlab/Simulink仿真环境中，按照以下参数搭建三相5电平仿真模型：各桥臂包含4个子模块，直流侧电压为800 V，调制波频率50 Hz，载波频率5 kHz，调制度为1，桥臂电抗为11 mH，负载由100 Ω的电阻和60 mH的电抗组成，仿真结果如图5～图7所示。

图5 输出相电压、相电流波形Fig.5 The waveforms of phase output voltage and current

图6 A相上桥臂子模块电容电压值Fig.6 The fluctuation of capacitance voltage of the submodulesinupperarmofphaseA

图7 桥臂电抗电压和Fig.7 The sum of the reactors′voltage in the arm

由图5可知，因桥臂子模块N为4，输出相电压波形为N+1=5电平，输出电平数与理论分析相符。输出相电压总谐波畸变率THD为24.72%，输出相电流基本无畸变。由图6可知，上桥臂4个子模块电容电压波动趋势相同且范围很小，为电容电压值的1.5%左右，均衡效果良好。

当每相处于投入的子模块个数保持为N时，因各桥臂电压和应与直流侧母线电压值相等，则各相上、下桥臂电抗的压降之和应为0，由图7可知，其与理论分析相符合。

4.2 输出相电压2N+1电平仿真分析

在Matlab/Simulink仿真环境中，按照5电平的参数搭建三相9电平仿真模型，仿真结果如图8～图10所示。由图8可知，输出相电压为2N+1=9电平，且随着电平数量的增加，输出相电压THD由原来的24.72%降低为12.72%，输出相电流波形也得到相应的改善，输出相电流几乎无畸变。

由图9可知，在输出相电压提高的同时，输出相电压2N+1电平的上桥臂4个子模块电容电压均衡效果和N+1电平基本一致。

图8 输出相电压、相电流波形Fig.8 The waveforms of phase output voltage and current

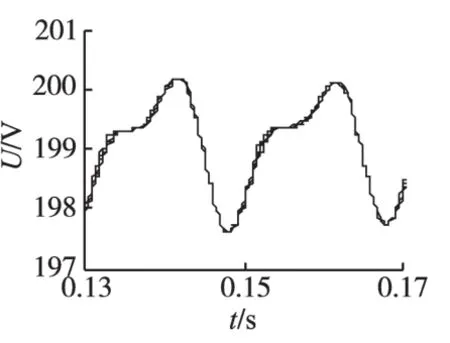
图9 A相上桥臂子模块电容电压值Fig.9 The fluctuation of capacitance voltage of the submodulesinupperarmofphaseA

图10 桥臂电抗值电压和Fig.10 The sum of the reactors′voltage in the arm

当桥臂中子模块投入的个数在N，N+1，N-1之间变化时，为保持直流侧电压的稳定，则各相上、下桥臂电抗的压降之和在0，-USM，USM之间变化，由图10可知，上、下桥臂电抗电压和在0，-200，200间变化，其与理论分析相符合。

5 实验分析与结论

在搭建的MMC单相样机上按照以下参数对输出相电压为N+1电平和2N+1电平的调制策略进行实验验证：各桥臂包含4个子模块，直流侧电压100 V，调制波频率50 Hz，载波频率5 kHz，调制度为1，桥臂电抗为5 mH，负载由50 Ω的电阻和15 mH的电抗组成。实验结果如图11、图12所示。

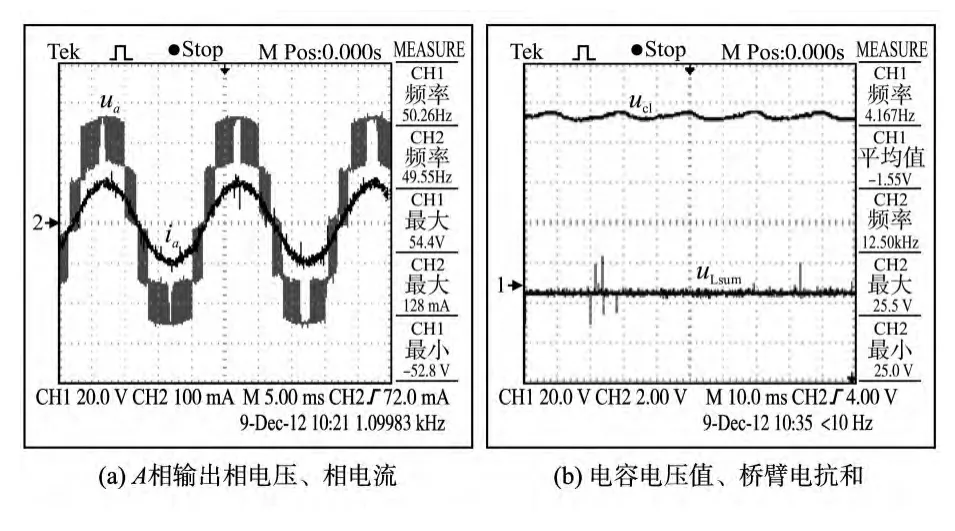
图11 N+1电平波形Fig.11 The waveforms of N+1 levels

图12 2N+1电平波形Fig.12 The waveforms of 2N+1 levels

图11为N+1电平波形图，因N为4，输出相电压为N+1=5电平，子模块电容电压值在25 V左右波动，且上、下桥臂电抗电压和基本为0 V。图12为2N+1电平波形图，输出相电压为2N+1=9电平，子模块电容电压波动与N+1电平基本一致，上、下桥臂电抗电压和在0，-25，25之间变化。

本文基于载波层叠技术，在分析各相投入的子模块数量的基础上提出了如何实现输出相电压为N+1电平与2N+1电平的调制策略，该调制策略无需数学计算，且子模块电容均压时只需排序，实现简单，易于MMC扩展到任意电平数目，仿真和实验结果验证了调制策略的可行性。

［1］Glinka M.Prototype of Multiphase Modular-mutilevel-converter with 2 MW Power Rating and 17-level-output-voltage［C］//In Power Electronics Specialists Conferece ，Aachen，Germany，2004：2572-2576.

［2］Lesnicar A，Marquardt R.An Innovative Modular Multilevel Converter Topology Suitable for a Wide Power Range［C］//In Power Tech Conference Proceedings，Bologna Italy：IEEE，2003：6.

［3］刘钟淇，宋强，刘文华.新型模块化多电平变流器的控制策略研究［J］.电力电子技术，2009，43（10）：5-7.

［4］Li Zixin.An Improved Pulse Width Modulation Method for Chopper-cell-based Modular Multilevel Converters［J］.IEEE Transactions on Power Electronics，2012：3472-3482.

［5］管敏渊，徐政，屠卿瑞，等.模块化多电平换流器型直流输电的调制策略［J］.电力系统自动化，2010，34（2）：48-51.

［6］王晓鹏，杨晓峰，范文宝，等.模块组合多电平变换器的脉冲调制方案对比［J］.电工技术学报，2011，26（5）：28-33.

［7］管敏渊，徐政，屠卿瑞，等.模块化多电平换流器环流抑制控制器设计［J］.电力系统自动化，2010，34（18）：57-61.

［8］廖其艳，郭家虎，赵埕萱.新型模块化多电平变换器的PWM控制［J］.电气传动，2011，41（9）：34-37.