基于功率反馈的直驱式永磁发电机组最大功率跟踪控制

，，，

（1.舰船综合电力技术国防科技重点实验室，湖北武汉 430033；2.西安交通大学电气工程学院，陕西西安 710049）

直驱式永磁风力发电系统采用风轮机与永磁同步发电机转子直接相连的方式，利用全容量变频器实现并网发电，更易于实现低电压穿越技术，对电网波动的适应性更好，功率控制也更灵活。同时，由于直驱永磁发电系统省去了电刷、滑环和齿轮箱等部件，因此系统结构得以简化，提高了发电效率和运行可靠性，在今后的大型变速恒频风力发电系统中将有广阔的研究应用空间［1-3］。

风能的不确定性以及风轮机自身特性会使风力发电机输出功率随风速变化而波动，同时，这也会给风力机转速的测量带来很大的困难。为提高风能的利用效率，需使风力机任意风速下运行在最佳转速，从而吸收最大的风能。文献［4］提出一种通过直接检测风速，依据风力机特性曲线实时计算出发电机转速，采用速度闭环控制的方案。但该方案需要增加高精度的风速检测设备，可这会附带着系统的可靠性的降低；另外，由于风力机周围气流受叶片扰动较大，风机叶片上各点风速都不相同，因此难以准确测量当前有效风速。文献［5］提出了一种基于功率给定的最大风能捕获跟踪策略，该策略通过对发电机定子磁场定向矢量的解耦控制，控制发电机的有功功率和无功功率来实现对风力机的输出功率控制。文献［6］通过控制发电机从传动轴上吸收的机械转矩与转子转速符合最佳转矩曲线，来实现最大风能捕获。文献［7］提出以定子端有功功率为控制量，通过功率闭环控制，引入前馈解耦控制，利用功率平衡关系得到最大风能点的最大风能捕获跟踪策略。但是，在传统的基于功率反馈的最大风能捕获控制策略中，一般采用磁场的定向矢量控制发电机输出功率进行调节风机转速，这就必须保证风力机转速和转子位置检测的精确性。通常，实现的方法是在电机轴上安装光电编码器等传感器测量转子位置和风力机的转速，但随之会带来测量精度、环境适应性不强、转子转动惯量增大以及不能保证光电编码器的零刻度与转子磁极初始位置一致等系列问题。

本文分析了风力机自身的运行特性，建立永磁同步发电系统数学模型，在变流器的控制策略上，引入前馈解耦控制和软件锁相环，无需测量装置就可得到风力机转速，根据发电机当前转速变化的情况实时计算最佳功率。通过控制直驱永磁风力发电机的电磁功率来间接控制风力发电机转速以追踪风力机最佳功率曲线，无需检测风速实现对最大风能的捕获以及风力发电系统的单位功率因数控制。最后，建立基于双PWM变换器的直驱永磁同步风力发电实验系统，通过模拟仿真，验证了所采取策略的有效性。

1 基于功率反馈的最大风能捕获原理

1.1 风力机运行特性

风力机从叶片扫过的面积中析取风能为

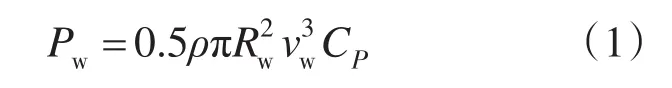
式中：ρ为空气密度；ρ=1.225 kg/m3；Rw为风轮的半径；vw为上风向自由风速；CP为风力机的功率析取系数。

CP的值与桨距角和叶尖速比有关，其数学表达式为

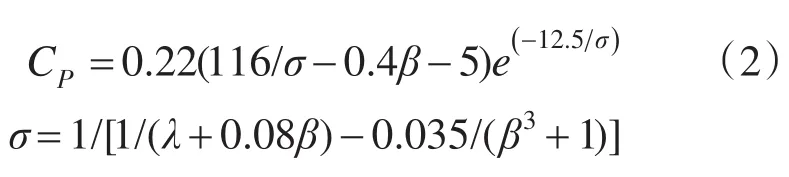
式中：β为桨距角；λ为叶尖速比，λ=Rwωw/vw；ωw为风力机风轮的转速。

某一风速下，当桨距角β保持恒定时，为使风力机析取的机械功率达到最大，需要调节发电机的转速ωw使CP达到最大值CPmax，从而实现最大功率跟踪控制，这时所对应的叶尖速度比λ是唯一的，设为λopt，则风力机析取风能的最大值为

式中：kopt为使得风力机析取风能达到最大值的系数，其数值表达式为

风力机的功率—转速特性曲线如图1所示。

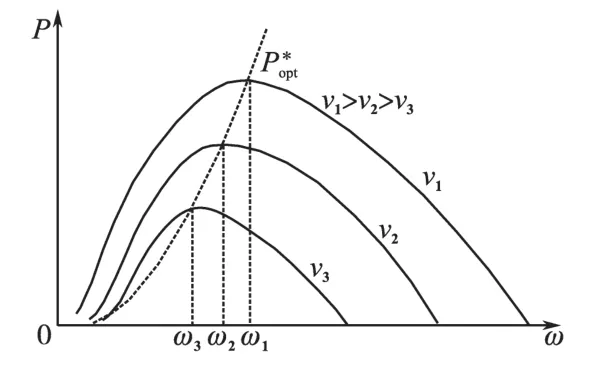
图1 风力机功率—转速特性曲线Fig.1 Wind turbine power-speed characteristic curves

1.2 功率反馈控制原理

实现最大风能跟踪的要求是在风速变化时及时调整风力机的转速，使其始终保持最佳叶尖速，从而保证系统运行于最佳功率曲线上［8］。对风机转速的控制可通过风力机变桨调节，也可通过控制发电机输出功率进行调节。由于风力机变桨调节系统结构复杂，调速精度较低，本文通过变流器控制发电机输出电磁功率来调节发电机转速。

图2所示为基于功率反馈的风电系统最大风能跟踪控制。通过锁相环可以得到风力机的转速，根据风力机的最大功率曲线，计算出与该转速所对应的风力机的最大输出电磁功率，将它作为风力机的输出功率给定值P*e，并与发电机输出功率的观测值Pe相比较得到误差量，经过调节器对风力机进行控制，以实现对最大风能捕获。

图2 功率反馈跟踪控制示意图Fig.2 Power feedback tracking control diagram

1.3 锁相环原理

由于直驱式永磁发电机转子与风力机经过传动轴直接相连，发电机转子转速与风力机转速相等，所以，发电机的电磁功率可表示为

由式（4）可知，发电机实际输出的电磁功率与其转子转速有关。为此，采用了软件锁相环对转子转速进行测量。软件锁相环是一种自适应闭环系统，能够实时跟踪三相对称电源的频率与相位［9］。通过锁相环无需测量工具就可以得到发电机的转子转速。软件锁相环原理结构框图如图3所示。

图3 SPLL原理结构框图Fig.3 SPLL schematic block diagram

图3中，发电机输入机侧变流器的三相电压经坐标变换后得到Uq。取参考值=0，与Uq比较后的差值，经过PI控制器和滤波器滤波，得到发电机的转子转速，即无需通过光电编码器等测量工具就可以获得风力机的转速ωw，再经过积分环节，可以得到发电机的转子位置θ。

2 永磁风力发电系统的仿真模型

本文采用永磁风力发电系统模型由永磁同步发电机、机侧变流器、直流母线电容以及网侧变流器组成。发电机产生的电能，通过变流器的整流、逆变后，经过变压器，最后流入电网。

2.1 永磁同步发电机模型

以永磁体转子极中心线为d轴，沿转子旋转方向超前90°（电角度）为q轴，dq坐标系随转子同步旋转。定子基于发电机惯例来规定各个物理量的正方向，建立dq0坐标系下PMSG数学模型为

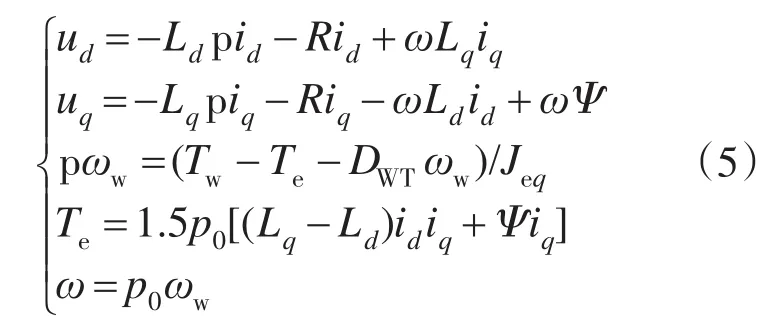
式中：p为微分算子；ud，uq，id，iq分别为永磁同步发电机的d，q轴电压，d，q轴电流；Ld，Lq分别为PMSG的d，q轴电感；R为PMSG定子电阻；p0为PMSG的极对数；Ψ为转子永磁体的磁链最大值；Jeq，DWT分别为发电机组的转动惯量和阻尼系数；Tw，Te分别为PMSG的风力转矩和电磁转矩；ω为PMSG的电角速度。

2.2 机侧变流器

式中：s1d,s1q分别为dq坐标系下的机侧变流器开关量；iL为直流侧负载电流；ud,uq分别为发电机端口电动势的d，q轴分量；id,iq分别为交流电流的d，q轴分量；v1d,v1q分别为机侧变流器输入三相电压矢量的d，q分量。

机侧变流器的d轴变量和q轴变量间存在耦合，给控制器的设计带来困难，为此采用前馈解耦控制策略：

式中：s为拉普拉斯微分算子；kiP，kiI分别为PI控制器的比例、积分系数。

联立式（6）和式（7）可得：

这样，通过前馈算法实现了对电流的解耦控制。

锁相后u1q=0，相应的i1d为有功电流，i1q为无功电流。iq的参考值i*q取为0，实现单位功率因数整流。id的参考值i*d由永磁同步发电机实际电磁功率与MPPT算法得到参考电磁功率比较后的差值，经过PI控制器运算后给出。机侧变流器控制策略如图4所示。

我国区域的广阔性，造就了农村文化的多样性，主要表现在音乐、舞蹈、戏曲、诗歌、传说、信仰等方面，音乐舞蹈有北方的秧歌、南方的花灯，戏曲有北方的河北梆子、秦腔和南方的粤剧、越剧、绍剧、黄梅戏、豫剧等，还有曲艺、说唱、相声、滑稽戏等，云贵地区的傩戏，历史久远，已成为重要的信仰民俗。家庭联产承包责任制实行以后，一味的追求商品生产，暴露了文化引导力度的不足，许多丰富的音乐、舞蹈、传说、信仰等文化形式难以为继。直至社会主义新农村建设的目标提出以后，这种状况才有所转变。

图4 机侧变流器控制策略Fig.4 The machine-side converter control strategy

2.3 网侧变流器

网侧变流器承担着维持直流母线电压基本恒定，将风力机发出的功率传送到电网侧的任务，其运行性能直接决定了送向电网的电能质量，也决定了整个风力发电系统的运行性能。其拓扑结构与机侧相似，采用电压矢量定向原理，可得到网侧变流器的数学模型为

式中：s2d,s2q分别为dq坐标系下的网侧变流器开关量；iL为直流侧负载电流分别为电网侧三相交流电动势的d，q轴分量分别为交流电流的d，q轴分量；v2d,v2q分别为网侧变流器输入三相电压矢量的d，q轴分量。

同样，网侧变流器的d轴变量和q轴变量间存在耦合，需要采取前馈解耦控制策略：

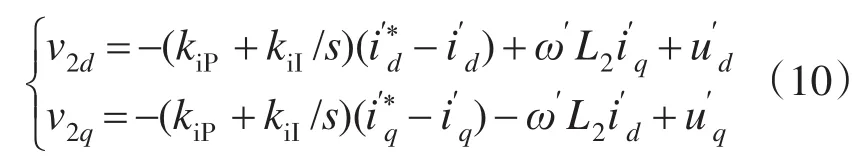
联立式（9）和式（10）可得解耦控制方程为

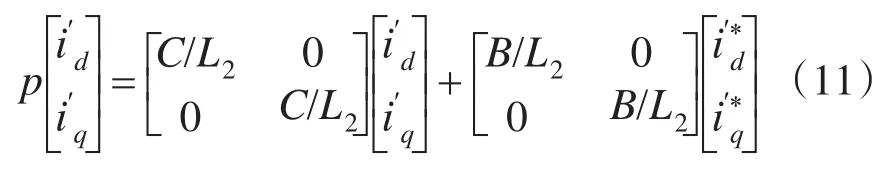
其中

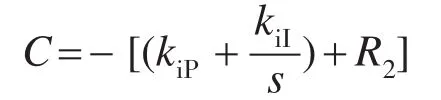
对其控制思路与机侧变流器相似，区别在于原来机侧变流器的功率外环控制改为电压外环控制，控制策略如图5所示。采用锁相环对q轴分量进行锁相，锁相后=0，相应的为有功电流为无功电流。的参考值取为0，实现单位功率因数逆变。的参考值由直流电容参考电压与当前直流母线电压Udc比较后的差值，经过PI控制器运算后给出。

图5 网侧变流器控制策略Fig.5 Network side converter control policy

3 仿真结果及分析

3.1 系统仿真参数及设置过程

为验证本文采用控制方案的可行性，采用Matlab/Simulink软件进行了系统仿真。仿真参数如下。

风力机参数为：风轮半径Rw取42 m，风力机等效转动惯量6.25×106kg⋅m2，转动粘滞系数DWT取为0。桨距角β=2°，当风速达到vw=11.38 m/s，功率析取系数达到最大值CPmax=0.402时，风力机的输出功率达到额定功率2 MW。

PMSG参数为：永磁磁链Ψ=10.23 Wb，等效转动惯量8 000 kg·m2，直轴电感Ld=1.3 mH ，交轴电感Lq=2.3 mH（插入式转子结构Ld＜Lq），发电机定子等效电阻R=0.013 3 Ω，电机磁极对数p0=30。

变流系统参数为：滤波电感L=250 μH，滤波电感寄生电阻Rr=0.12 mΩ，直流母线电压Udc=1 100 V，直流电容C=28.8 mF。

自然风由慢速变化分量和快速变化分量［10］组成，其中基本风表示慢速变化分量，阵风和噪声风速组成快速变化分量，阵风是快速变化分量的主要组成部分。整个仿真过程设置时长为70 s，模拟自然风速变化如图6所示，风速的变化共分为4个阶段：t=0 s时，初始风速从0 m/s阶跃至8.5 m/s；0～25 s期间，保持基本风速为8.5 m/s，运行风电系统到稳定状态；当t=25 s时，加入噪声风；在t=45 s时，基本风速由8.5 m/s阶跃至10.35 m/s。

图6 风速变化曲线Fig.6 Change of wind speed curve

3.2 仿真实验结果

图7为风力机叶尖速比在变风速下的情况；图8为风力机功率析取系数变化曲线。可以看出，在t=25 s时，风速从8.5 m/s骤升至10.35 m/s，功率析取系数CP有一个短暂小跌落后，能够较快地恢复到最大值0.402附近并保持稳定。同样风力机叶尖速比短暂跌落后能较快恢复并保持在最佳叶尖速比λ=7.32附近，风力机模型能够很好地响应风速快速的变化，最大功率跟踪效果良好。

图7 风力机叶尖速比Fig.7 Tip speed ratio of the wind turbine

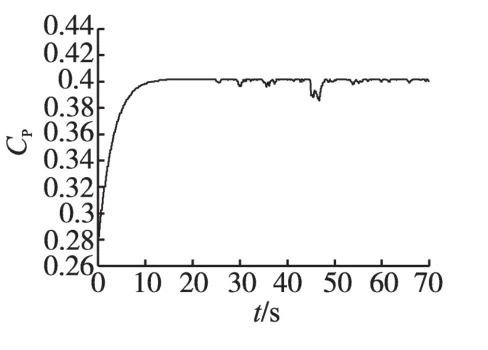
图8 风力机功率析取系数Fig.8 Wind turbine power coefficientofdisjunctive

图9为风力机实际转速；图10为锁相环估计转速；图11为转速的误差。由图9～图11看出，通过锁相环跟踪风力转速效果良好，转速估计误差限制在0.2 rad/s以内。

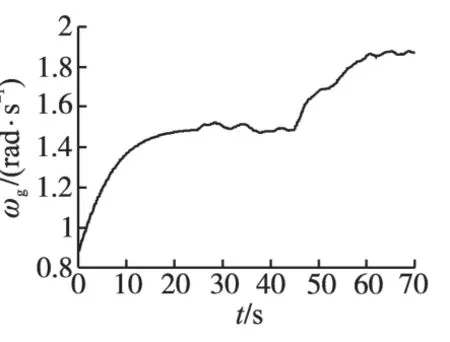
图9 风力机实际转速Fig.9 The actual speed of the wind turbine

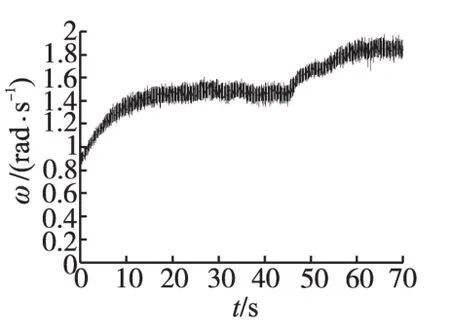
图10 估计转速Fig.10 Estimated speed

图12为直驱式永磁同步发电机输出的电磁功率变化曲线，对比图9所示风力机的转速变化曲线，可以看出，通过机侧变流器的功率反馈控制，控制电磁转矩Te，使得风机转速ωw追踪风速变化，永磁同步发电机输出的电磁功率随着风力机转速ωw的上升而增加，很好地响应了风力机转速的变化。

图11 转速误差Fig.11 Speed error

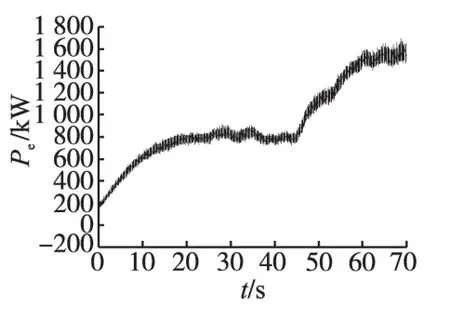
图12 永磁发电机电磁功率曲线Fig.12 Electromagnetic power curve of PMSG

图13为网侧变流器单相电压和单相电流。由图13可知，在风速变化的情况下，发电系统连接电网侧的相电压和相电流始终保持反相位，网侧变流器锁相环锁相效果良好，实现了风电系统的单位功率因数控制。图14为直流侧电压，可以看出网侧变流器很好地稳定了直流母线电压，波动很小。

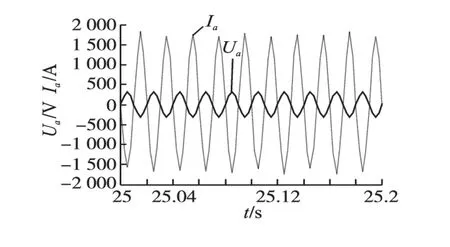
图13 网侧变流器输出单相电压和单相电流Fig.13 Single-phase voltage and single-phase current output in network-side converter

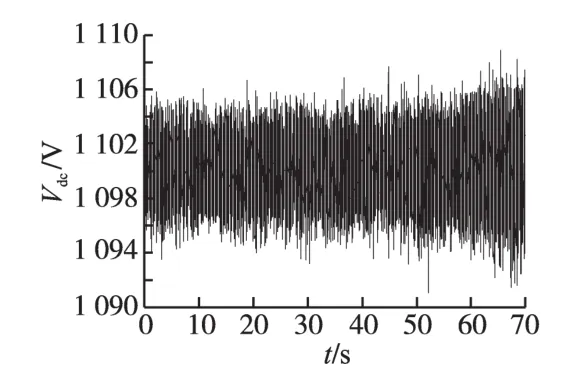
图14 直流侧电压Fig.14 DC voltage

4 结论

本文通过分析风力机特性，基于功率反馈控制原理，建立了双PWM变换器的直驱式永磁风力发电系统的数学模型，通过变流器的有效控制，无需测量风速和风力机转速就可实现永磁同步发电机的单位功率因数控制和风能的最大功率跟踪。同时，很好地满足了变速恒频的要求，可为直驱式永磁发电并网系统保持供电稳定提供控制技术手段，具有较好的效果和更好的实用价值。

［1］El Mokadem M，Courtecuisse V，Saudemont C，et al.Experimental Study of Variable Speed Wind Generator Contribution to Primary Frequency Control［J］.Renewable Energy，2009，34（3）：833-844.

［2］陈明亮，肖飞，王颢雄，等.直驱型永磁同步风力发电机无传感器控制［J］.电机与控制学报，2009，13（6）：792-797.

［3］Mauricio J M，Marano A，Gomez-exposito A，et al.Frequency Regulation Contribution Through Variable-speed Wind Energy Conversion Systems［J］.IEEE Trans.Power Syst.，2009，24（1）：173-180.

［4］Moor G D，Beykes H J.Maximum Power Point Trackers for Wind Turbines［C］//IEEE 35th Annual Power Electronics SpecialistsConferenceAachen，Germany：IEEE，2004：130-136.

［5］胡家兵，贺益康，刘其辉.基于最佳功率给定的风能追踪控制策略［J］.电力系统自动化，2005，29（24），32-38.

［6］姚骏，廖勇，瞿兴鸿，等.直驱永磁同步风力发电机的最佳风能跟踪控制［J］.电网技术，2008，32（10）：11-15.

［7］曾志勇，冯婧，周宏范.基于功率给定的双馈风力发电最大风能捕获策略［J］.电力自动化设备，2010，30（6）：25-30.

［8］汤天浩，陈新红，彭东恺，等.直驱式永磁同步发电机稳态模型与最大功率跟踪控制［J］，电源学报，2011，19（3）：13-20.

［9］琚兴宝，徐至亮，邹建龙，等，基于DSP的三相软件锁相环设计［J］.通信电源技术，2004，21（5）：1-4.

［10］Anderson P M.Bose A.Stability Simulation of Wind Turbine Systems［J］.IEEE Transactions on Power Apparatus and Systems.1983，102（12）：3791-3795.