基于自适应高斯滤波的电站历史数据稳态检测方法

高 萌， 刘吉臻， 王瑞琪， 张 恒， 张 轩

（1.华北电力大学 控制与计算机工程学院，北京102206；2.中国石油管道科技研究中心，河北廊坊065000）

电厂机组的性能评价、运行优化和系统建模等均需要获得稳态工况下的历史数据，而目前主要采用现场试验来获得样本数据.随着信息化技术的高速发展，电厂在线监测系统中存储了海量数据信息［1－3］，但由于电站负荷处于变化状态，实时历史数据库中混杂着大量非稳态运行数据.相比于传统实验方法，从历史数据库中提取稳态数据不需对研究对象外加扰动，可以避免现场试验对实际生产的影响，而且工作周期短［4－5］.

目前国内外有关电站历史数据稳态检测问题的研究较少，普遍采用针对过程变量建立的稳态评价指标来进行稳态判断，且方法大多建立在具体工业过程基础上，不具有普遍适用性［6－8］.基于数据的稳态检测方法是针对数据变化趋势的研究，不需考虑检测对象的机理特征.现有的基于数据的稳态检测方法主要有基于统计学理论和基于趋势提取两类方法.组合统计检验法（CST）［9］、置信度法（MTE）［10］和R检验法［11］等均建立在统计学理论上.此类方法主要通过对检测数据划分等量区间，利用区间方差或均值来建立统计量，结合假设检验以判断稳态.采用不同的数学理论对检测数据进行趋势提取，进而构建稳态检验量，确定适当的阈值进行稳态判断的方法即为基于趋势提取的稳态检测方法，如小波分析法［12］、自适应多项式滤波法［13］和 BP神经网络法［14］等.由于采用假设检验进行判断，基于统计学理论的方法得到的是稳态与否的检测结果，而基于趋势提取的方法可给出具体接近稳态的量化程度.稳态检测结果的准确性对阈值的依赖度很高，基于趋势提取的方法阈值的确定需建立在历史稳态数据基础之上，而基于统计学理论的方法给出了确定置信度下阈值确定的理论方法，相比较而言，基于统计学理论的稳态检测方法具有更高的可靠性.稳态检测方法各有优劣，需结合具体情况进行选择.

稳态检测方法对数据波动敏感，而由于仪表安装位置、布线和环境等多种因素的影响，监测到的数据信号中含有噪声.对数据进行去噪处理可以有效地提高检测结果的准确性.笔者引入一种基于高斯滤波器的自适应去噪算法［10］对电站历史数据稳态检测问题进行研究.

1 稳态检测原理

历史数据库中混杂了大量变化状态，从中检测出趋势平缓的数据区域即称为稳态检测.如图1所示，x（t）在［t1，t2］内的数据为稳态数据.

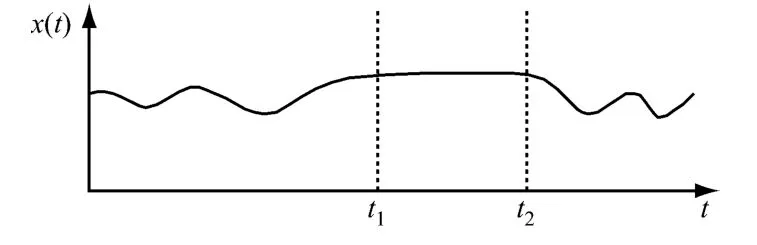
图1 稳态检测示意图Fig.1 Schematic diagram of the steady－state detection

本文稳态检测原理如图2所示.高斯噪声是检测信号中常见的一类噪声，对应的高斯滤波器克服了传统滤波片相位移动和设计复杂的缺点.但传统的高斯滤波器对信号进行相同的处理时易平滑掉突变信息，而发生突变的区域必然处于非稳态，突变信息的保留对稳态检测结果的准确性有很大影响.笔者选用的基于高斯滤波器的自适应去噪算法具有良好的去噪效果且突变信息保留能力较高，可在滤去噪声的同时最大程度地保留原始信号的变化信息.

图2 稳态检测流程图Fig.2 Flow chart of the steady－state detection

相比于基于趋势提取的方法，基于统计学理论的方法在检测阈值的确定上具有更加可靠的理论依据.组合统计检验法和置信度法等基于统计学理论的方法需要对信号划分时间区间，并假设区间内为稳态，仅在区间之间状态发生变化，因此所检测出的稳态数据区域的边界不准确，区域划分对数据长度有要求，对于实时更新的数据库，每次更新均需要重新划分区域，因此也不能进行在线检测.而Rhinehart等提出的R检验法不采用时间窗处理数据，利用变量滤波前后方差估计值的比值来构建稳态检验量，从而进行稳态判断.R检验法是对相邻两时刻点的状态变化进行判断，且每一时刻检验量的计算仅与上一时刻的测量值、滤波值和方差估计值等有关，占用的存储空间小，计算速度快，适用于在线检测.另外，Rhinehart等对相关参数和阈值的选取还进行了统计分析及仿真［11］，方法的可靠性较高.因此，笔者选取R检验法进行电站历史数据的稳态检测.

2 自适应高斯滤波器

2.1 高斯滤波器的基本原理

高斯滤波器的基本思想是将高斯核函数与原始信号进行卷积得到滤波输出后的信号［15］.设一维高斯函数为

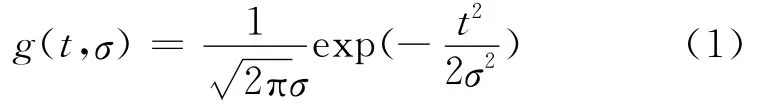
其一阶导数为

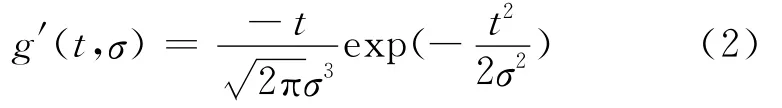
式中：g′（t，σ）称为高斯滤波器.

函数f（t）滤波后的结果为

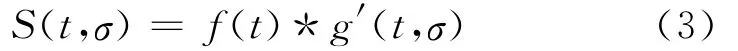
式中：“＊”为卷积运算符；σ为高斯函数的标准方差，为恒定参数.

2.2 算法原理

设m为采样时间点；f（m）为历史数据信号；fk＋1（m）为第k＋1次迭代平滑滤波后的输出值；wk（m＋j，σ）为窗内各点的权值；滤波窗长度为2 M＋1（M为非0整数）.则有

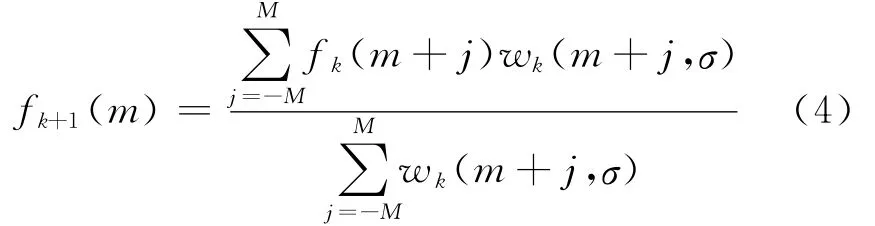
权值wk（m）是影响滤波效果的关键参数.当时，由式（4）推得，即滤波器对全部信号序列进行了平滑，突变点信息未被保留；当， 突变点信息得到了保留.为满足突变点信息保留和信号平滑的双重需求，利用模板中心点的导数来自适应调整滤波器的权值，避免了人工调整权值的繁琐程序，即

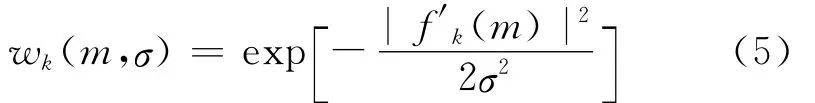
式中：k为迭代次数；f′k（m）为信号值fk（m）的一阶导数.

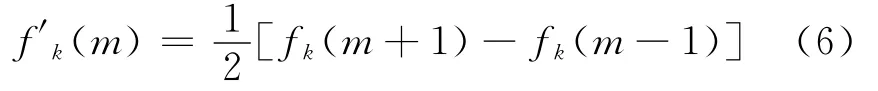
一阶导数f′k（m）与σ的比值决定了权值wk（m，σ），改变参数σ的取值可以控制去噪后信号的平滑程度和突变点信息的保留程度.

2.3 参数性能

唐良瑞等［15］仿真分析了 wk（m，σ）取值对滤波器效果的影响，得出如下结论：当wk（m，σ）较大，即σ＞f′k（m）时，若干次迭代后，去噪效果明显，但会平滑掉突变点信息；当 wk（m，σ）较小，即σ＜f′k（m）时，若干次迭代后，不能实现去噪目的，反而会放大包括突变点信息在内的噪声信息；当wk（m，σ）近似为0，即σ≈f′k（m）时，迭代运算后，突变点信息可以得到保留，且去噪效果良好.

另外，信号滤波后的平滑程度随迭代次数k的增加而增强.滤波窗长度越长，即M取值越大，则滤波效果越平滑，但取值不宜过大，否则会使结果过于平滑，失去原始信号的波动特性.

2.4 实现步骤

图3给出了基于高斯滤波器的自适应去噪算法的具体实现步骤.参数M根据需设置的滤波窗口大小进行设置，考虑尽量保留突变点信息以及序列点相互关联的特点，采用1×5模板进行滤波，因此令M＝2.

算法具体实现步骤如下：

（1）计算信号f（m）的长度L，即取样点个数.

（2）设置迭代次数K，初始化次数标志量k＝0.

（3）计算信号每点的导数值f′k（m），并求取所有点导数的平均值.

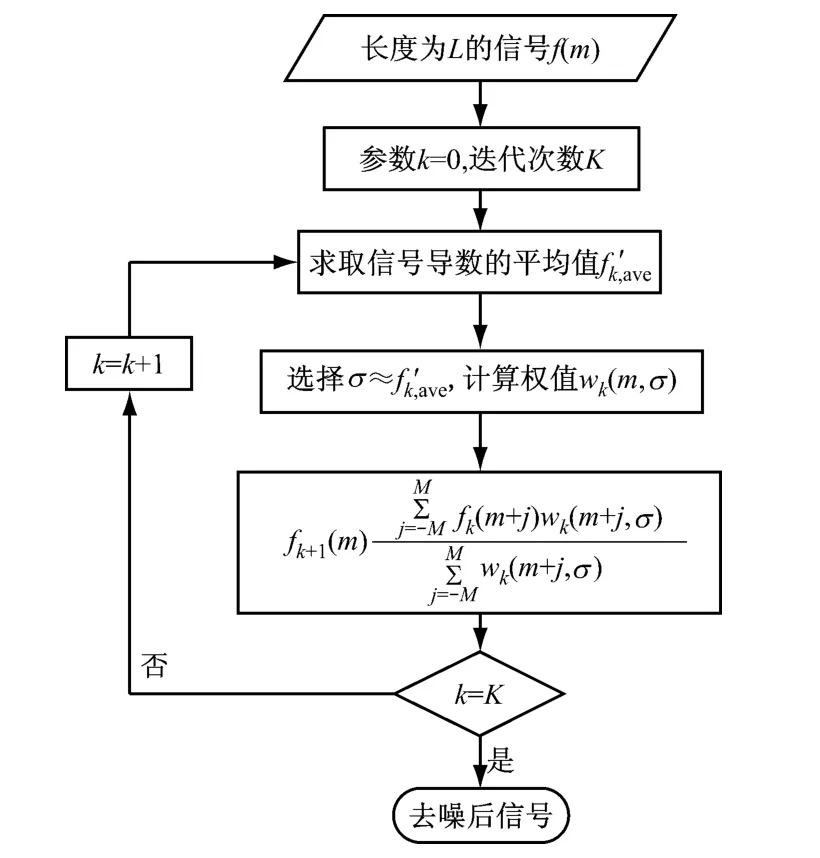
图3 自适应高斯滤波去噪算法流程Fig.3 Flow chart of the de－noising algorithm based on adaptive Gauss filter

（5）判断迭代次数，若k＝K，结束迭代，否则令k＝k＋1，用当前滤波后的数据代替原始数据，继续执行步骤（3）.

3 R检验法

3.1 检验原理

设待检测时间序列X第i时刻的测量值为xi，滤波系数设为λn∈（0，1］（n＝1，2，3）；利用式（7）和式（8）分别计算一阶滤波后的滤波值xf，i和均方差；然后利用某时刻第i序列测量值xi与前一时刻第i－1序列测量值xi－1，根据式（9）计算方差的无偏估计.

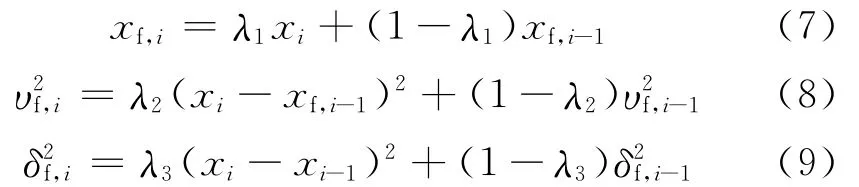
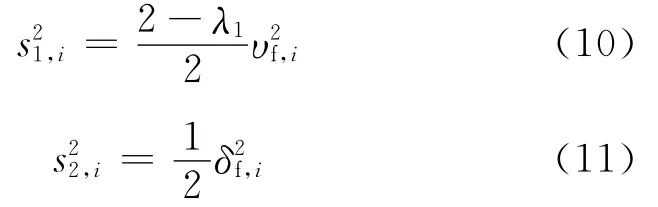
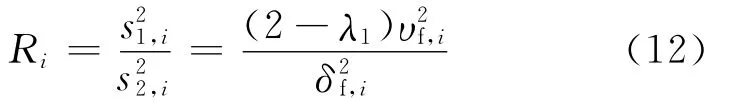
Rhinehart等通过理论和仿真分析给出了在确定的置信度α下阈值Rcrit和滤波系数λn的推荐取值表.通过比较Ri和Rcrit可以检测过程变量是否处于稳态.当Ri＜Rcrit时，过程变量处于稳定状态，记状态标志量Ssi＝1；当Ri＞Rcrit时，过程变量处于非稳态，记为Ssi＝0.

3.2 参数性能分析

为分析参数选取与检测效果之间的关系，仿真生成一组服从正态分布的时间序列数据（10 000点），改变滤波系数λn的取值，由式（7）～式（12）分别计算出每组取值下对应的统计量R，并绘制R的概率密度函数分布图（见图4）.图中λ1、λ2和λ3的取值共有4组，分别为：（1）λ1＝0.1，λ2＝0.1，λ3＝0.1，标记为（0.1，0.1，0.1）；（2）λ1＝0.01，λ2＝0.01，λ3＝0.01，标记为（0.01，0.01，0.01）；（3）λ1＝0.1，λ2＝0.01，λ3＝0.01，标记为（0.1，0.01，0.01）；（4）λ1＝0.01，λ2＝0.1，λ3＝0.1，标记为（0.01，0.1，0.1）.

分析图4中的概率密度分布趋势可知：λ1的取值对R值概率分布的影响很小，主要影响因素为λ2和λ3的取值；λ2和λ3取值增大，则R的概率分布相对分散，且R的取值范围增大.Rhinehart等［16］给出了置信度为0.05下的推荐取值：滤波系数λ1＝0.2，λ2＝0.1，λ3＝0.1，检测阈值Rcrit＝1.44.

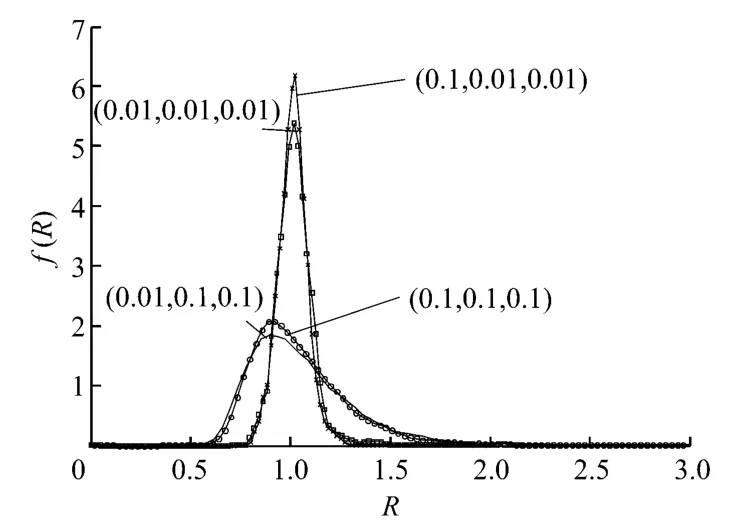
图4 不同滤波系数对R值概率密度分布的影响Fig.4 Probability density function of Rat different filter factors

但是在实际仿真应用中发现，对于不同的检测对象，推荐参数取值不能保证检测结果均符合期望，因而对滤波系数取值做进一步分析.设置λ1、λ2和λ3为以下3种取值组合：（1）λ1＝0.2，λ2＝0.1，λ3＝0.1，标记为（0.2，0.1，0.1）；（2）λ1＝0.2，λ2＝0.1，λ3＝0.01，标记为（0.2，0.1，0.01）；（3）λ1＝0.2，λ2＝0.01，λ3＝0.1，标记为（0.2，0.01，0.1）.

3种滤波系数取值组合所对应R值的概率密度分布曲线见图5.由图5可知，在相同阈值下，当λ2＝λ3时，R值的概率分布过于集中，易于出现第II类错误；当λ2＜λ3时，R值的概率分布更离散，临界值较小的情况下易于出现第I类错误.因而，最终选择滤波系数取值为：λ1＝0.2，λ2＝0.1，λ3＝0.01.

3.3 检测步骤

基于前述分析，结合基于高斯滤波器的自适应去噪算法进行信号的稳态检测，具体步骤如下：

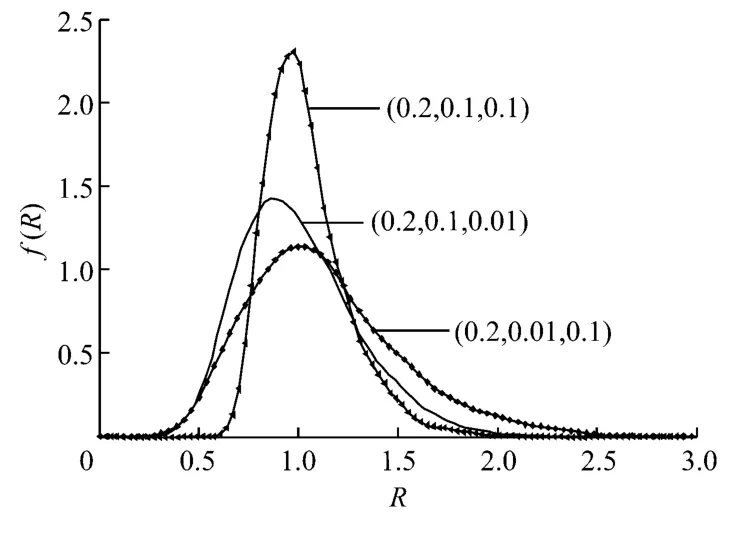
图5 滤波系数具体取值分析Fig.5 Analysis for determination of filter factors

（1）将采用基于高斯滤波器的自适应去噪算法处理后的信号作为待检测对象X.

（2）初始化滤波值xf，i、均方差以及方差的无偏估计，取序列前10个测量值的平均值作为滤波值的初始值xf，0，其方差为均方差初始值取.

（3）确定检测参数取值：滤波系数λ1＝0.2，λ2＝0.1，λ3＝0.01，检测阈值Rcrit＝1.44.按序列时间顺序，根据式（7）～式（12）顺次计算统计量R.

（4）比较Ri和Rcrit，当Ri＜Rcrit时，状态标志量记为Ssi＝1；当Ri＞Rcrit时，记为Ssi＝0.

（5）状态标志量Ssi＝1所对应的原始数据序列区域即为稳态部分.

将上述检测过程称为基于自适应高斯滤波的稳态检测方法.

4 电站历史数据的稳态检测

选取某电厂1 000MW机组总风量历史数据对检测方法的有效性进行验证.选取1 000点数据，采样时间为3s，如图6所示.R检验法取置信度为0.05，确定滤波系数λ1＝0.2，λ2＝0.1，λ3＝0.01，检测阈值Rcrit＝1.44.对该组样本数据先后采用中值滤波法和基于高斯滤波器的自适应去噪算法进行处理，2种方法均选用1×5模板.

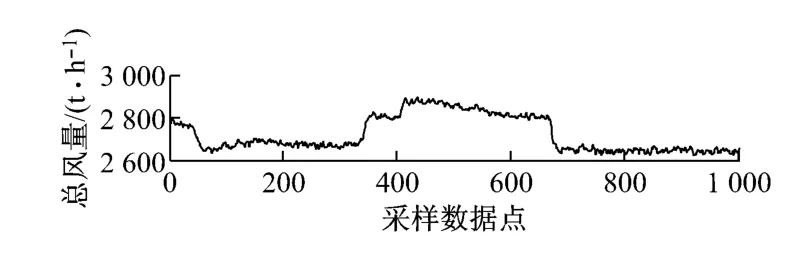
图6 某电厂1 000MW机组总风量历史数据Fig.6 History data of total air volume in a 1 000MW unit

图7和图8分别为采用2种滤波方法进行稳态检测的仿真图像.其中（a）图为采用不同滤波方法处理后的风量数据；（b）图为对应时刻点稳态检测变量R值的变化情况；（c）图为根据阈值Rcrit＝1.44进行稳态判断后的检测结果，状态标志量为1的区域对应为稳态区域，状态标志量为0的区域对应为非稳态区域.

对比图7（a）与图8（a）滤波后的总风量数据曲线可以看出，在选用相同大小滤波模板的情况下，对于同一样本数据的去噪效果，基于高斯滤波器的自适应去噪算法要优于中值滤波法.在采样数据点i为45、334、403和661等风量曲线发生突变的位置，与图7（a）相比，在图8（a）中对应数据点处的趋势突变幅度更大，因此采用基于自适应高斯滤波的稳态检测方法可以有效提高下一步稳态检测边界的精确性.

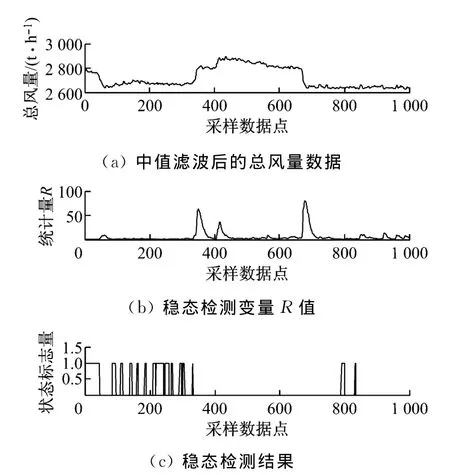
图7 采用中值滤波去噪的稳态检测Fig.7 Steady－state detection based on median filter

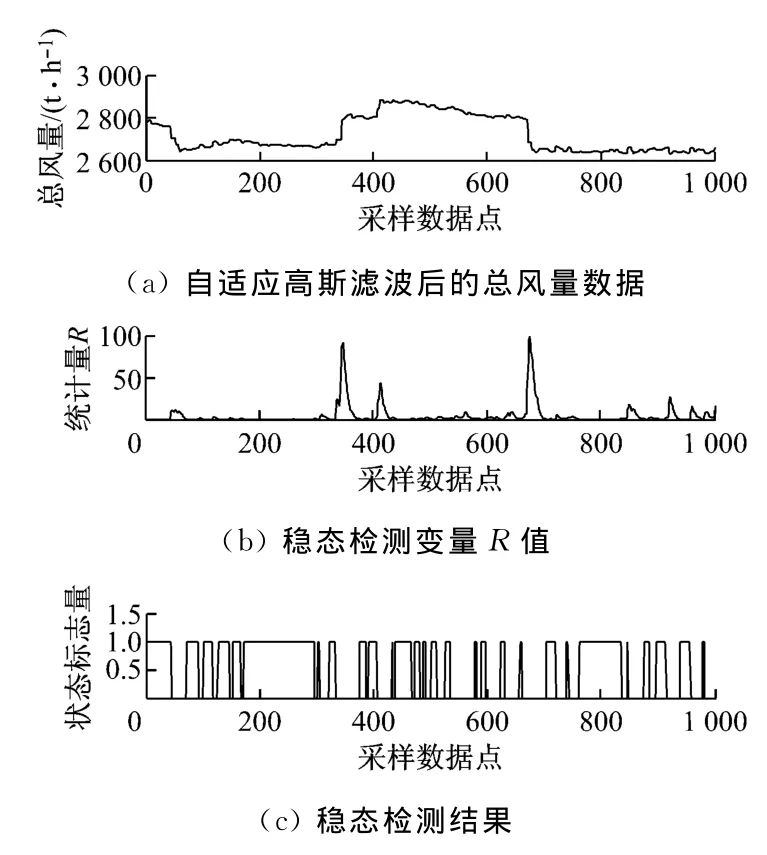
图8 基于自适应高斯滤波的稳态检测Fig.8 Steady－state detection based on adaptive Gauss filter

对比分析图7（b）与图8（b），在［45，83］、［334，374］、［403，440］和［661，701］等数据曲线处于波动状态的区域，显然图8（b）中R值的尖峰幅值相对较大，且平稳区域检验量R的取值远远小于波动区域R的取值，因而平稳区域与波动区域的边界更加清晰，说明基于高斯滤波器的自适应去噪算法对突变点信息的保留能力优于中值滤波法，状态转换边界清晰也有效降低了利用阈值进行稳态判断发生误判的可能性.

由图7（c）与图8（c）可以看出，应用基于高斯滤波器的自适应去噪算法进行稳态检测对检测效果的提高有较大贡献.图8（c）的检测结果中有［70，297］和［760，836］等较长时间的稳态区间，而图7（c）对应范围内的稳态区域狭小且分散，结合图7（a）与图7（b）分析可知，中值滤波法的去噪效果不佳，使得表征趋势波动情况的R值偏大，因而发生了将稳态区域检测为非稳态区域的误判情况.

对比分析以上2组仿真结果，基于自适应高斯滤波的稳态检测方法可以有效去除待检测信号中的噪声干扰，对趋势波动的突变点信息保留能力较强.与采用中值滤波的稳态检测方法相比，对较短区域的稳态具有更高的灵敏度，而且对稳态与非稳态区域的边界点识别更准确.

5 结束语

电站在线监测系统所存储的历史数据是对机组运行情况的最真实反映，并且包含全工况、多因素下的各种数据.从海量的历史数据中提取稳态数据，可以为热工对象建模和优化控制等相关研究提供大量数据信息.笔者首先选用基于高斯滤波器的自适应去噪算法对电站在线监测历史数据进行消噪处理，然后采用具有较高可靠性和计算速度的R检验法进行稳态检测.选取某1 000MW机组的总风量数据，对方法的有效性进行了仿真验证，并在选择相同滤波模板和相同检测方法的前提下，对本文方法和采用中值滤波的稳态检测方法进行了对比分析.仿真结果表明，本文的稳态检测方法具有更高的检测灵敏度和准确度，并且具有较快的运算速度，相较于其他的稳态检测方法，更适合进行在线检测，对于实际工况运行的实时状态监测与操作维护等工作具有很重要的现实意义.

［1］周洪煜，张振华，陈晓锋，等.应用径向基函数神经网络－信息融合方法改进超临界锅炉燃料量控制［J］.动力工程学报，2010，30（11）：833－837.ZHOU Hongyu，ZHANG Zhenhua，CHEN Xiaofeng，et al.Application of RBFNN－data fusion method to improvement of supercritical boiler fuel flow control［J］.Journal of Chinese Society of Power Engineering，2010，30（11）：833－837.

［2］赵征，刘伟，刘吉臻，等.基于信息融合的锅炉燃烧优化技术［J］.动力工程，2009，29（1）：53－56.ZHAO Zheng，LIU Wei，LIU Jizhen，et al.Combustion optimization technique of boiler based on information fusion［J］.Journal of Power Engineering，2009，29（1）：53－56.

［3］杨红权，陶丽，丁士发，等.电站锅炉炉内壁温测量技术的研究［J］.动力工程，2009，29（8）：717－721.YANG Hongquan，TAO Li，DING Shifa，et al.Study on measuring technology for tube wall temperature in the furnace of utility boilers［J］.Journal of Power Engineering，2009，29（8）：717－721.

［4］谷俊杰，高建峰.基于动态特性机理分析的带再热汽温状态观测器控制系统的研究［J］.动力工程学报，2011，31（2）：109－114.GU Junjie，GAO Jianfeng.Study on control system with reheat steam temperature state observer based on dynamic characteristic analysis［J］.Journal of Chinese Society of Power Engineering，2011，31（2）：109－114.

［5］李超顺，周建中，向秀桥，等.基于超平面原型聚类的水轮机调速系统模糊模型辨识［J］.动力工程，2009，29（4）：363－368.LI Chaoshun，ZHOU Jianzhong，XIANG Xiuqiao，et al.Fuzzy model identification of hydro－turbine governing system with clustering based on hyperplane prototype［J］.Journal of Power Engineering，2009，29（4）：363－368.

［6］程浩斌，周怀春，娄新生.新型燃煤锅炉燃烧过程稳定性评价指数 CSI［J］.工程热物理学报，1997，18（4）：512－516.CHENG Haobin，ZHOU Huaichun，LOU Xinsheng.A new combustion stability index CSI for utility coalfired boilers［J］.Journal of Engineering Thermophysics，1997，18（4）：512－516.

［7］赵虹，杨建国，常爱英，等.煤粉燃烧稳定性指数的建立［J］.燃烧科学与技术，2003，9（4）：364－366.ZHAO Hong，YANG Jianguo，CHANG Aiying，et al.Establishment of combustion stability index of pulverized－coal［J］.Journal of Combustion Science and Technology，2003，9（4）：364－366.

［8］刘吉臻，杨光军，谭文.一种基于数据驱动的电站状态稳定性能评价指标［J］.热力发电，2008，37（1）：45－49.LIU Jizhen，YANG Guangjun，TAN Wen.An index based data－driven for evaluating the state stability in power plant［J］.Thermal Power Generation，2008，37（1）：45－49.

［9］NARASIMHAN S，MAH R S H，TAMHANE A C，et al.A composite statistical test for detecting changes of steady states［J］.American Institute of Chemical Engineering Journal，1986，32（9）：1409－1418.

［10］NARASIMHAN S，CHEN S K，MAH R S H.Detecting changes of steady states using the mathematical theory of evidence［J］.AICHE J，1987，33（11）：1930－1932.

［11］CAO Songling，RHINEHART R R.An efficient method for on－line identification of steady state［J］.Journal of Process Control，1995，5（6）：363－374.

［12］JIANG Taiwen，CHEN Bingzhen，HE Xiaorong，et al. Application of steady－state detection method based on wavelet transform［J］.Computers ＆Chemical Engineering，2003，27（4）：569－578.

［13］付克昌，戴连奎，吴铁军.基于多项式滤波算法的自适应稳态检测［J］.化工自动化及仪表，2006，33（5）：18－21.FU Kechang，DAI Liankui，WU Tiejun.Method of adaptive steady－state detection based on polynomial filtering［J］.Control and Instruments in Chemical Industry，2006，33（5）：18－21.

［14］毕小龙，王洪跃，司风琪，等.基于趋势提取的稳态检测方法［J］.动力工程，2006，26（4）：503－506.BI Xiaolong，WANG Hongyue，SI Fengqi，et al.A method based on tendency distillation for ascertaining state steadiness［J］.Journal of Power Engineering，2006，26（4）：503－506.

［15］唐良瑞，祁兵，杨雪，等.一种基于高斯滤波器的电能质量信号去噪算法［J］.中国电机工程学报，2006，26（10）：18－22.TANG Liangrui，QI Bing，YANG Xue，et al.A denoising method of power quality signal based on Gaussian filter［J］.Proceedings of the CSEE，2006，26（10）：18－22.

［16］CAO Songling，RHINEHART R R.Critical values for a steady－state identifier［J］.Journal of Process Control，1997，7（2）：149－152.