导管螺旋桨不同桨叶的叶梢泄露涡分析
2014-09-21周军伟王大政
周军伟,王大政
(哈尔滨工业大学(威海)船舶与海洋工程学院,264209山东威海)
导管螺旋桨作为一种先进的船舶推进器,具有推力大、效率高、噪音低等优点[1].已有研究表明,当导管螺旋桨工作于高负荷情况下,其空化首先发生在叶梢附近[2-3],且梢涡空化是其主要的空化形态[4-5].Rains[3]的进一步研究表明,叶梢泄露涡(short of tip leakage vortex,TLV)的空化是梢涡空化的主要形式,而其他梢涡空化大多由于局部分离导致,能够通过桨叶局部导圆而消除.因此,探讨叶梢泄露涡的流动机理对深入研究导管螺旋桨的空化具有十分重要的意义.Chen等[6]基于相似理论推导了不可压流中TLV的轨迹,但没有考虑叶梢间隙的影响;张军等[7]对TLV的速度场进行了测量,Oweis等[8]以及 Wu 等[9]对梢涡空化进行了研究;Park 等[10]、朱志峰等[11]以及Wang等[12]采用求解 NS 方程[10-11]或面元法[12]进行了数值研究.
关注叶梢泄露涡的涡核压力以及与之相关的叶梢泄露流、速度环量[13]等流动参数,对于深入了解导管螺旋桨叶梢泄露涡的空化机理,探索推迟空化的方法具有十分重要的意义.
为了深入探索叶梢泄露涡的流动机理,本文将探讨不同桨叶设计参数对TLV涡核压力与轨迹的影响.桨叶设计参数将选取螺距比与盘面比来展开研究.同时,由于不同桨叶下导管螺旋桨叶梢流场将发生变化,对比分析不同叶梢流场下叶梢泄露涡、叶梢泄露流及叶梢翼型负荷之间的关联关系.本文选取导管螺旋桨19A/Ka4-55作为基准桨叶进行研究,采用CFD方法对导管螺旋桨的流场进行模拟.
1 导管螺旋桨的设计
1.1 基准导管螺旋桨
基于荷兰MARIN实验室的19A/Ka4-55导管螺旋桨展开研究.该导管桨采用19A导管,其设计长径比为0.5;4片桨叶,设计盘面比0.55.采用的基准桨叶螺距角为0.963,该桨叶的敞水性能曲线已经通过实验测量得到,可以用于数值方法的校验.
本文采用的导管在19A导管的基础上进行加长,使其能够适应具有更大盘面比与螺距角的桨叶.导管长径比在原来的基础上增加一倍,加长后的导管定义为19AL2,与19A的外观对比如图1所示,二者的外壁面都为锥面.19AL2/Ka4-55导管螺旋桨的整体外观如图2所示.

图1 导管19A与19AL2的几何对比

图2 19AL2/Ka4-55导管螺旋桨的外观
1.2 不同桨叶的设计
保持翼型不变,采用等螺距角设计,得到不同螺距比的桨叶;将不同半径处的翼型沿弦向等比例拉伸,保持桨叶最大厚度不变,得到不同盘面比的桨叶.
本文在常用螺距比与盘面比范围内选取了若干设计参数进行分析,如表1所示,螺距角0.963、盘面比0.55的桨叶为基准桨叶.
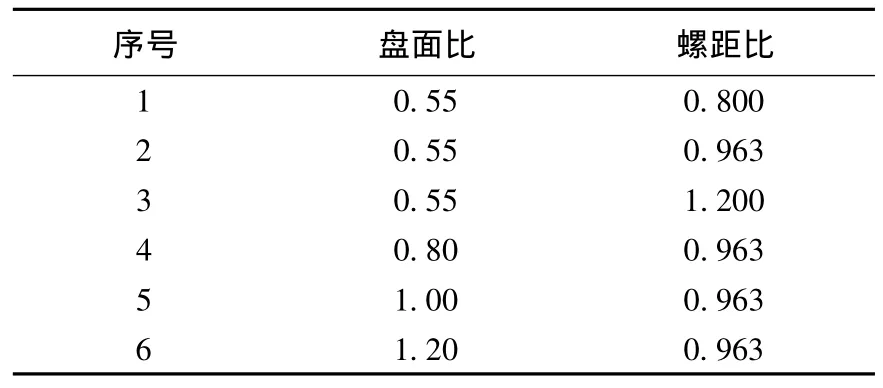
表1 不同盘面比与螺距比的列表
2 数值方法
导管螺旋桨完全浸入水中,且不受自由液面的影响,因而可以将绝对压力分解为相对压力与水压头,即在方程求解的过程中仅求解相对压力,而在分析流场时加上水压头即可得到绝对压力.
模拟循环水槽中的实验状态,导管螺旋桨固定位置转动,通过控制来流速度实现不同进速系数.来流方向与螺旋桨轴线平行,且压力、速度均匀分布,因而相邻螺旋桨叶片周围流场满足周期性边界条件.为了节省计算量,在数值计算过程中仅模拟1/4的流场.
将管螺旋桨的流动域分为螺旋桨周围的旋转域I与其他范围的固定域II,如图3所示,分别在旋转坐标系与固定坐标系下对两个域的流动进行求解.两个域的接触面采用转静交界面边界条件.

图3 网格区域划分与边界条件
采用混合网格对流场进行离散,以保证导管壁面有足够密的附面层网格.流场子午面网格如图4(a)所示,图中旋转域中的网格为周期性边界网格在子午面的投影.为了使求解域的上、下游边界与半径方向边界上流动尽量均匀,固定域II的范围在螺旋桨前方、后方及半径方向分别为10倍、20倍、10倍螺旋桨直径.该流域充分延伸,能够保证边界流动的均匀性[14].螺旋桨桨叶周围划分附面层网格,如图4(b)所示,为50%半径处回转面网格.为了更加清楚地显示网格质量,图中结构化网格的每个序列仅给出了1/4的网格点.图4(b)中给出的翼型前缘与尾缘的网格为实际加密状态.壁面网格尺寸控制在y+<1.0.
边界条件如图3所示,进口给定轴向速度,出口给定静压,所有物面包括叶片表面、导管表面与轮毂表面,都为无滑移边界,外边界给定速度矢量.
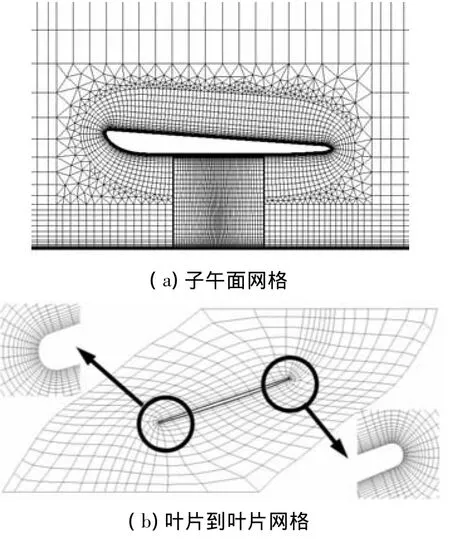
图4 导管螺旋桨流场网格
用Ansys公司的CFX 13.0软件对模型流场进行求解,其采用的方法为求解雷诺平均NS方程.湍流模型选用k-ε模型.为了与性能曲线实验情况相对应,螺旋桨转速选为2.5 r/s,得到不同进速系数下的导管螺旋桨性能参数如图5所示,图中实验数据来源于Kuiper的研究报告[15].为了验证不同网格疏密度对计算结果的影响,对比了60万、80万与100万网格时导管螺旋桨的性能参数,可以看出,不同网格下螺旋桨性能的模拟结果基本一致,并且与实验结果吻合.其中,推力系数与扭矩系数的误差在3%以内,效率误差在高进速系数区域较大,在设计点附近能够保证误差在5%以内.由于缺少该导管螺旋桨流场的详细测量,这里仅给出了性能校验.

图5 导管和螺旋桨的性能曲线
由于本文将针对叶梢泄漏涡流场进行分析,因此对漩涡流场的分辨率要求较高.本文中所采用的数值方法能够清晰地分辨导管螺旋桨叶梢常见的叶梢泄漏涡与叶梢分离涡等漩涡结构.
3 结果与讨论
在以往的研究中发现,导管螺旋桨在启动状态下最容易发生空化,本文中给出的导管螺旋桨都工作在临近零进速情况下.
3.1 TLV涡核压力的分布
图6为TLV涡核空化数沿叶梢翼型弦向的分布曲线.不同弦向位置的压力值选取为当地垂直弦向截面上的最低压力.相对空化数σ为

式中prel为相对压力,即涡核压力相对等水深无穷远处压力.由于导管桨通常工作在固定转速下,而当进速发生变化时,桨叶翼型相对速度也会发生变化,而叶梢切线速度保持不变,因而这里选取叶梢切线速度U为参考速度.图中s为当前截面至叶梢翼型前缘的距离,c为叶梢翼型弦长.

图6 不同桨叶参数下叶梢泄露涡空化数沿叶梢弦向分布
图6(a)中给出的是盘面比为0.55,不同螺距比情况下的TLV涡核空化数分布.可以看出,当螺距角增大,涡核空化数曲线明显降低.随着螺距比的增大,最低空化数快速降低,螺距比从0.800增加到0.963的过程中,涡核最低空化数降低了约42%;而从0.963增加到1.200的过程中,涡核最低空化数降低了约67%.随着螺距比的增大,最低空化数位置逐渐向叶梢前缘靠近,在螺距比为1.200的情况下,最低空化数位置出现在叶梢翼型前缘.
图6(b)给出了螺距比0.963时不同盘面比导管螺旋桨TLV涡核空化数的分布曲线.随着盘面比的增大,涡核空化数逐渐提升,最低空化数位置逐渐向叶梢前缘靠近,但最低空化数位置始终在20%~50%的弦长范围内,即最低空化数不会出现在叶梢前缘位置.
从图6可以看出,在大多数情况下,TLV涡核空化数沿叶梢弦向的分布曲线近似为抛物线.由于叶梢流场的复杂性,对这一现象还很难解释.
3.2 TLV的轨迹分析
了解TLV的发展轨迹是建立TLV水动力模型的基础[6].描述TLV轨迹的参数包括涡核中心至叶片吸力面的距离yc及涡核中心至叶梢的距离zc.由于在对TLV流场的分析中发现TLV形成的环形流线中心与最低压力点并不重合,如图7所示,难以确定涡核中心位置,因而以下分别给出了这两点的坐标值.
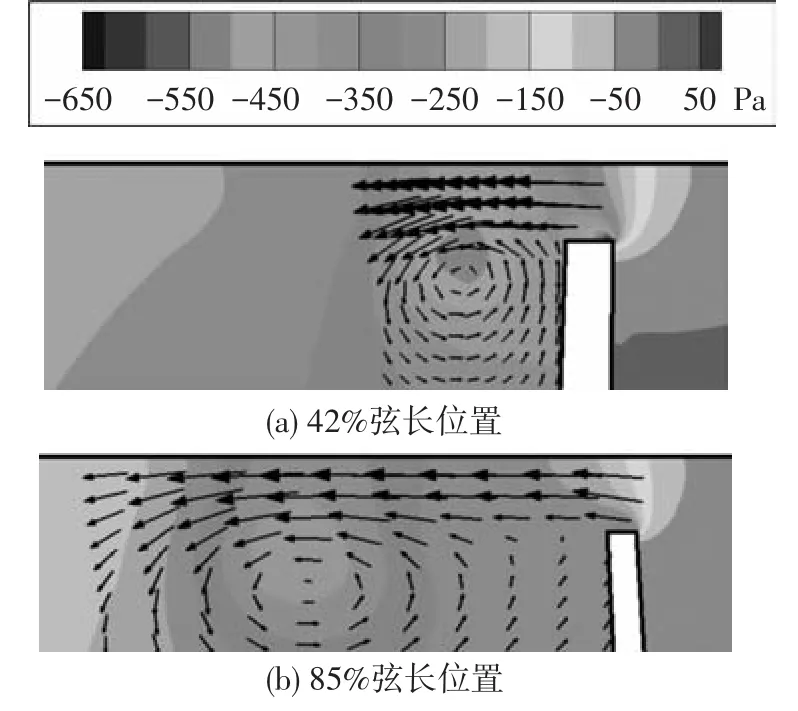
图7 TLV的压力云图与速度矢量图
图8分别给出了TLV环形流线中心点与最低压力点的两个坐标沿叶梢弦向的分布曲线.图中坐标yc采用叶梢翼型弦长c进行无量纲化,用于描述在blade-to-blade面上TLV涡核轨迹与叶片之前的夹角;zc采用叶梢间隙τ来进行无量纲化,用于描述TLV至叶梢的距离大小.
从图8(a)中可以看出,随着桨叶螺距比的增大,TLV逐渐远离桨叶吸力面.在TLV向下游发展的过程中,yc值开始变化比较缓慢,越到下游增加越快,这一点在图8(b)不同盘面比的TLV轨迹中也能显示出来.图中每条yc曲线都包括两条紧靠在一起的曲线,其中一条为环形流线的中心点,另一条为最低压力点.可以看出,这两点的yc坐标变化曲线基本一致.从图8(b)中不同盘面比桨叶的TLV轨迹曲线可以看出,盘面比的变化对TLV的yc坐标变化几乎没有影响.
从图8(c)与(d)可以看出,最低压力点的分布曲线几乎不随桨叶的改变而发生变化.环形流线中心点的分布曲线随桨叶螺距比的增大以及盘面比的增大而增大,其沿弦向的分布规律近似为直线,距离叶梢的最大距离约为1倍叶梢间隙,距离叶梢的平均距离约为0.6~0.8倍的叶梢间隙.通过以上TLV zc坐标的无量纲分析可以得出:减小叶梢间隙能够降低TLV的影响半径范围,从而减小TLV对流道的堵塞;而增大盘面比同样会引起流道的堵塞,这也是引起螺旋桨效率降低的因素之一.

图8 不同桨叶的TLV轨迹曲线
3.3 TLV的流场分析
对TLV轨迹的分析发现,在垂直叶梢弦向的截面上环形流线中点与最低压力点并不重合.如果TLV为自由发展的漩涡,显然这两点应该重合.这种流场特点从侧边反映了TLV是一种受迫涡,而对其发生作用的是叶梢泄露流(short of tip leakage flow,TLF),这一点能够从图7中的速度矢量图上看出,TLF的流速明显高于TLV的流速,从而在二者的交接处产生剪切,改变了TLV的运动规律.
为了能够清楚的显示TLF与TLV之间的剪切作用,图9给出了基准桨叶在27%、56%、85%弦向位置截面的流线与涡量云图.可以看出,除叶梢分离涡位置外,最大涡量点近似与最低压力点重合,与环形流线的中心点有一定的偏差.这也说明最大剪切位置近似在最低压力点位置.

图9 基准桨叶垂直叶梢弦长截面上的流线图与涡量云图
另外,从图9还可看出,在叶梢间隙中,靠近叶梢的流场存在明显的剪切作用,表明该位置附面层与流动分离占据了主导地位;而靠近导管内壁的位置流场涡量几乎为零,几乎没有剪切流动.
3.4 TLF分析
叶梢泄露流的成因主要有两个方面:其一为桨叶相对导管内壁的运动,在相对坐标系下,相当于有以叶梢切线速度U流过间隙的流动;其二,由于桨叶两侧存在压差,因此迫使水从压力面向吸力面流动.除此之外,叶梢分离流与流体黏性等因素也会对TLF产生一定的影响.
图10给出了不同盘面比与螺距比桨叶的叶梢泄露流流速云图,图中RP为螺距比,RS为盘面比.图中所取截面为50%间隙处的圆柱面.虚线所示为叶梢翼型.来流速度自下而上,桨叶旋转自右向左.从图中可以看出:1)TLF速度最大值大部分出现在叶梢前缘附件位置,当桨叶螺距比变小时,TLF速度最大值逐渐向弦长中部靠近;2)随着螺距比的增大,TLF的速度迅速增大,螺距比从0.8至1.2的变化过程中,TLF的速度增大了约10%;3)随着盘面比的增大,TLF的速度逐渐降低,盘面比从0.55增大到1.20的过程中,TLF的速度降低了约5%.

图10 不同螺距比与盘面比桨叶叶梢泄露流速度云图
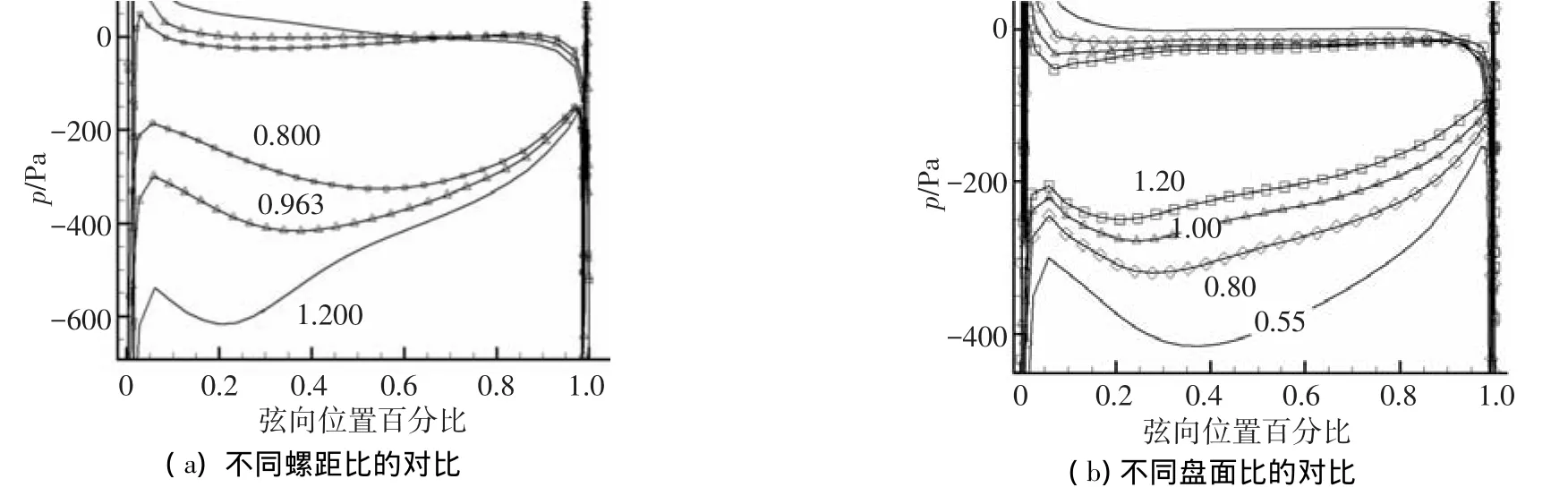
图11 不同螺距比与盘面比桨叶叶梢翼型压力分布曲线
分析TLF与叶梢翼型负荷的关联,图11给出了不同桨叶叶梢翼型表面的压力分布.为了排除叶梢绕流对桨叶表面的压力干扰,选取了距离叶梢半径1倍间隙处的翼型来进行分析.
从图11(a)可以看出,较大螺距比的桨叶吸力面压力较低,且最低压力点更靠近叶片前缘位置,约在20%弦长位置;螺距比为0.963的基准桨叶,其叶梢吸力面最低压力约在35%弦长位置;而螺距比为0.8的桨叶,其叶梢吸力面最低压力约在55%弦长位置.由于桨叶压力面压力几乎一样,显然3个桨叶两侧的最大压差位置基本与吸力面最低压力位置重合.对比该结果与图10(a)~(c)中叶梢泄露流的速度云图,可以发现,最大TLF速度的位置大致与叶梢桨叶两侧最大压差位置一致.
从图11(b)可以看出,较大盘面比的桨叶吸力面压力较高,且最低压力点更靠近叶片前缘位置.盘面比为0.55的基准桨叶,其最低压力位置约在35%弦长位置;盘面比为0.80的桨叶,其最低压力位置约在27%弦长位置;盘面比为1.00的桨叶,其最低压力位置约在23%弦长位置;盘面比为1.20的桨叶,其最低压力位置约在20%弦长位置.同样,由于桨叶压力面压力几乎一样,4个桨叶两侧的最大压差位置基本与吸力面最低压力位置重合.对比该结果与图10(d)~(f)中叶梢泄露流的速度云图,发现最大TLF速度的位置大致与叶梢桨叶两侧最大压差位置一致,这与不同螺距比桨叶中的现象一致.由此可以说明,TLF的大小变化主要与叶梢两侧压差相关.
4 结论
1)增大螺距比使TLV涡核空化数降低,且最低空化数位置向叶梢前缘靠近.在本文中螺距比为1.2的情况下,最低空化数位置移动到叶梢前缘.增大盘面比使涡核空化数提高,最低空化数位置同样向叶梢前缘靠近,但并不能达到叶梢前缘.
2)增大螺距比使TLV轨迹逐渐远离桨叶吸力面,但盘面比的变化几乎不会对TLV的yc坐标产生影响.TLV最低压力点的zc坐标几乎不随桨叶的变化而改变,但环形流线中心点的zc坐标随螺距比的增大而增大,随盘面比的增大同样增大.
3)叶梢泄露流与TLV之前存在明显的剪切作用,其速度明显高于TLV的外缘切线速度,这使得TLV的流线中心点与最低压力点并不重合.分析表明,最低压力点出现在最大涡量处.影响叶梢泄露流的主要因素为叶梢两侧压力,且最大叶梢泄露流速度的位置与最大压差位置基本一致.
[1]吴光林,严谨.船用螺旋桨的应用与发展趋势[J].广东造船,2008(4):49-51.
[2]朱月锐,席德胤.自然通气降低导管螺旋桨空泡噪声试验和理论分析[J].中国造船,1984(1):18-31.
[3]RAINS D A.Tip clearance flow in axial compressors and pumps[D]. [S.l.]:California Institute of Technology,Hydrodynamics and Mechanical Engineering Laboratories,1954.
[4]叶元培,周连第,郑永敏.导管螺旋桨空泡性能系列试验研究[J].中国造船,1980(4):27-41.
[5]CHESNAKAS C,JESSUP S.Tip vortex induced cavitation on a ducted propulsor[C]//Proceedings of the 4th joint fluids engineering conference.Hawaii:ASME,2003:257-267.
[6]CHEN G T,GREITZER E M,TAN C S,et al.Similarity analysis of compressor tip clearance flow structure[J].Journal of Turbomachinery,1991,113:260-269.
[7]张军,张志荣,朱建良,等.导管螺旋桨内流场的PIV测量[J].实验流体力学,2007,21(2):82-88.
[8]OWEIS G F,CECCIO S L.Instantaneous and timeaveraged flow fields of multiple vortices in the tip region of a ducted propulsor[J].Experiments in fluids,2005,38(5):615-636.
[9]WU H,SORANNA F,MICHAEL T,et al.Cavitation in the tip region of the rotor blades within a waterjet pump[C]//Proceedings of the Fluids Engineering Conference.Florida:ASME,2008:193-202.
[10]PARK W G,JUNG Y R,KIM C K.Numerical flow analysis of single-stage ducted marine propulsor[J].Ocean Engineering,2005,32(10):1260-1277.
[11]朱志峰,方世良,王晓燕.空化螺旋桨非定常粘性流场特征分析[J].中国科学:E辑,2011(2):213-222.
[12]WANG Guoqiang,LIU Xiaolong.A potential based panel method for prediction of steady and unsteady performances of ducted propeller with stators[J].Journal of Ship Mechanics,2007,11(3):333-340.
[13]BREWER W H,MARCUM D L,JESSUP S D,et al.An unstructured rans study of Tip-leakage vortex cavitation inception[C]//Proceedings of 4th Joint Fluids Summer Engineering Conference. Hawaii:ASME,2003:193-200.
[14]洪毅,赫晓东.复合材料船用螺旋桨设计与 CFD/FEM计算[J].哈尔滨工业大学学报,2010,42(3):404-408.
[15]KUIPER G.The Wageningen propeller series[M].Netherland:MARIN Publication,1992.
