关于微积分解题的两个注记

金少华， 王金环， 邢小玉， 宛艳萍， 王 东

(河北工业大学，天津300401)

微积分是理工科大学生的一门非常重要的基础课.在微积分的教学过程中，正面临着一个无法回避却又日益突出的矛盾：一方面，微积分课的学时普遍减少；另一方面，后续专业课及考研对学生学习这门课又有很高的要求.本文给出了微积分中求未定式极限时需注意采取的一个措施及由微分方程的通解求相应的微分方程的一般方法，并给出了算例，希望对读者能有所启发.

求未定式的极限是微积分教学中的一个重要内容.我们知道洛必达法则是求未定式极限的一种有效方法，但不是万能的，而且也未必是最简捷的，所以在求未定式的极限时能化简应尽可能先化简，可以应用等价无穷小替代或重要极限时，应尽可能应用，这样可以使运算简捷[1].这里指出：当未定式的分子或分母中出现f(b)-f(a)的形式时，先使用拉格朗日中值定理将f(b)-f(a)表为f′(ξ)(b-a)，一般情况下比直接用洛必达法则能大大降低题目的难度及复杂程度.

.

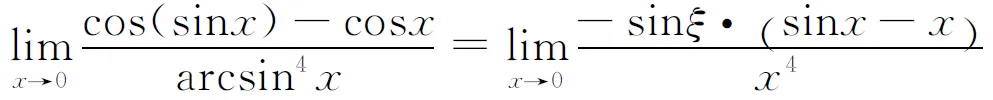
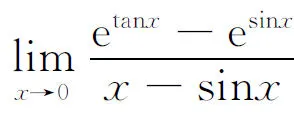
分析 本题含抽象函数f(x)，而且对f(x)除已知极限式外无任何信息，对本题不能使用洛必达法则.将cosx的带Peano余项的4阶麦克劳林公式代入已知极限式，是解此题的简捷方法.

注 在已知极限式中，设法分离出所要求的极限式，这是本题求解的关键所在.

下面用这种方法处理2008年全国考研数学一真题的第15题.

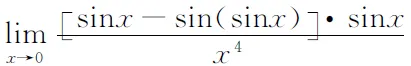
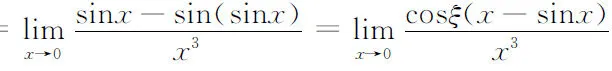
微分方程在几何、物理及数学建模中有重要应用[2].下面给出由微分方程的通解求相应的微分方程的一般方法.由于常微分方程的阶数、常微分方程中所出现未知函数最高阶导数的阶数、常微分方程通解中任意常数的个数及常微分方程初始条件的个数这四者是相等的，故应从常微分方程通解中所含任意常数的个数n确定方程的阶数n，对通解y=fx,c1,…,cn连续对x求导n次，得方程组

由该方程组解出c1,…,cn(用x,y′,…,y(n)表示)，并将其代入通解的表达式y=fx,c1,…,cn，便得所求方程.

例6求以函数x-c12+(y-c2)2=c2为通解的微分方程，其中c1,c2与c均为任意常数.

解在x-c12+(y-c2)2=c2中含有三个任意常数，所求方程必为三阶微分方程，因此必须将该式两边对x连续求导三次，得

x-c1+(y-c2)y′=0,

1+(y-c2)y″+y′2=0,

(1)

(y-c2)y‴+3y′y″=0.

(2)

[参 考 文 献]

[1] 同济大学应用数学系.微积分[M].北京：高等教育出版社,2002.

[2] 高等学校工科数学课程教学指导委员会本科组.高等数学释疑解难[M].北京：高等教育出版社,1992.