数学教辅书中的一类极值问题解答错误及修正

杨合俊

(长安大学理学院, 陕西西安710064)

1 引 言

近几十年来，各种微积分教辅书、考研数学复习指导书，层出不穷，这说明中国的大学教育、研究生教育得到了蓬勃的发展，也说明青年学生们日益重视对数学的学习.笔者最近就一个实际生活中的极值问题，查阅了一些相关的书籍，发现该题及其变形，作为导数与微分的应用，出现在各种版本的数学教辅书中. 但是，编者们提供的解法，有的违反了科学精神，主观臆断，导致了错误的结论；有的缺乏深入分析，结果自相矛盾.

2 一些高等数学辅导书中一类极值问题及其解答的分析

2.1 主观臆断，导致错误结论的解答

问题1大衣柜能搬进新居吗[1](1997年出版的《高等数学应用205例》中的第59例)：

老张临搬家前，站在自己大衣柜旁发愁.担心这大衣柜搬不进新居，站在一旁的小李马上拿了一把尺子出去了.不一会儿，小李对老张说：“从量得电梯前楼道和单元前楼道宽度，绝对没问题”.请问小李的根据是什么?

原书提供了如下解答(有删节)：

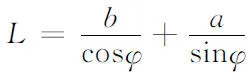
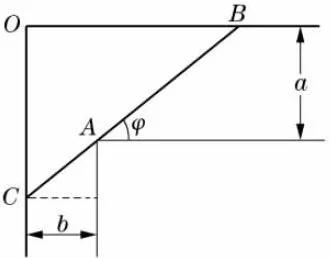
图1 搬运示意图

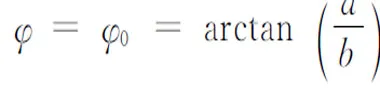
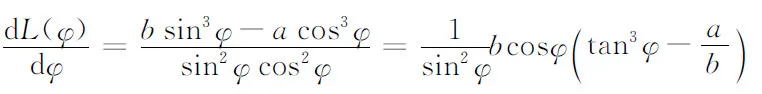
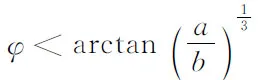
可是，现在却出现了一个问题：根据我们的生活经验，长度过大的大衣柜无法转过楼道拐角，客观上，确实存在着一个能够转过楼道拐角的大衣柜的最大值，而我们算出的却是最小值，那么，问题出在哪里呢？

实际上，根据生活经验，如果某一成功地转过了楼道拐角的大衣柜的长度恰好是最大的，那么，在转动它的最艰难的时刻，这个大衣柜的两端在某两点B，C处紧挨外侧墙壁，同时中部紧挨拐角A(如图1中所示)，这时点B、点C间的距离是经过拐角A且两端点分别在外侧墙壁上的线段的长度的最小值.若大衣柜的长度比这个值稍微大上一丝一毫，都会被卡死，不能转动，所以能转过楼道拐角的大衣柜，其长度当然不能超过这一数值，因而这一数值就是能转过楼道拐角的大衣柜的长度的最大值.

在这一实际问题中，相互垂直的两楼道的宽度是确定的，因而两端点分别在外侧墙壁上且经过拐角A的线段的长度是确定的，它是转角φ的一元函数，它有一个最小值，大衣柜能否转过楼道拐角，受制于这一最小值.因而，我们应该将研究对象转换为上述的线段，设其长度为y，则

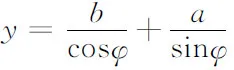
解出的y的最小值，就是能转过楼道拐角的大衣柜的长度的最大值.

2.2 缺乏深入分析，结果自相矛盾的解答

类似的题目还出现在马进业于1987年编的《高等数学典型试题分析》中，原题与解法如下(有删节)：

问题2[2]向宽为a米的河修建一条宽为b米的运河，二者成直角相交.问能驶进运河的船的最大长度为多少？

分析 求一个量的最大值，必须把该量写为某个量的函数.自变量的选取要由具体问题确定.本题求船长的最大值，船长与河宽a和运河宽b有关，而这种关系是通过角度α联系着的.所以应把船长s写成α的函数：

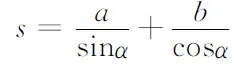
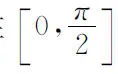
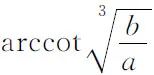
可见，编者并没有对该问题作深入的探究，当解出船长的最小值后，没有陈述这个最小值与能驶进运河的船的最大长度有何关系，解答就结束了.对于出现的矛盾，无视其存在，没有给出令人信服的解释.

为什么编者解得的结果与答案是矛盾的呢？事实上，如前所述，根源在于编者对该问题中量之间的关系，没有作深入的研究.

其实，该题目更早出现于1980年，是由费定晖、周学圣编演的《数学分析习题集题解(二)》(吉米多维奇著)中的第1587题[3]，编者提供了简短的解答，是正确的.

2.3 问题的变形中自相矛盾的解答

在王寿生于1996年主编的《考研数学常见题型分析及模拟试题》中，该题以下面的一个变化形式出现：

问题3[4]宽为a的走廊与另一走廊垂直相交.如果长为8a的细杆能水平地运过拐角，问另一走廊的宽度至少是多少?

题后提供了如下解法：

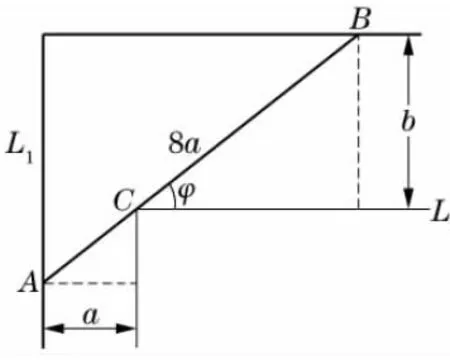
图2

解设另一走廊宽为b，细杆与壁夹角为φ(见图2)，则

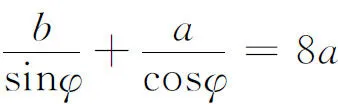
于是

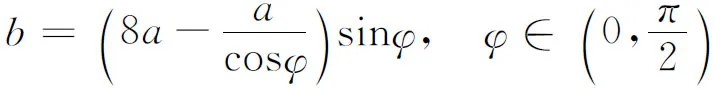
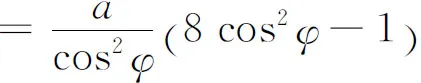
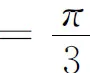
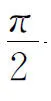
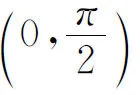
事实上，在这一问题中，已知走廊的宽度a是一定的，长为8a的细杆可理解为必须通过的消防设施(只是过长了些)，而另一走廊的宽度有待设计者确定.根据生活经验，另一走廊越宽，则细杆越容易通过，怎么可能有最大值的限制！但是，编者的计算并没有出错，那么，问题出在哪里呢？

其实，在编者给出的函数

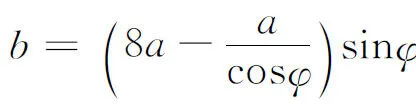
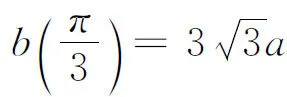
同样的题目以及类似的自相矛盾的解法还出现在参考文献[5-9]中.

[参 考 文 献]

[1] 李心灿. 高等数学应用205例[M].北京:高等教育出版社,1997:101.

[2] 马进业.高等数学典型试题分析[M].长沙： 湖南科学技术出版社，1987:204.

[3] 费定晖,周学圣.数学分析习题集题解(二)(吉米多维奇)[M].济南：山东科学技术出版社，1980:523.

[4] 王寿生.考研数学常见题型分析及模拟试题[M].西安：西北工业大学出版社,1996:28.

[5] 张孟秋.工科数学综合训练与应试指南(上册)[M].长沙：中南工业大学出版社,1997:208.

[6] 车向凯,谢崇远,王学理,孙艳蕊,付连魁,孔庆海.高等数学(上册)[M].沈阳：东北大学出版社，2005:.158-159.

[7] 陆子芬.高等数学解析大全—理论·问题·方法·技巧[M]. 沈阳：辽宁科学技术出版社，1991:227.

[8] 邵士敏.2001年研究生入学考试数学应试指导工学类[M]. 北京：北京大学出版社，2000：230.

[9] 王荷芬,王健生,归行茂,李重华,邵漪漪,桂子鹏,柴常智,曹助我.高等数学试题汇解(1978-1989)[M]. 上海：同济大学出版社，1990:215.