从几何的角度看微分中值定理
2014-09-22曾可依
曾可依
(重庆大学数学与统计学院,重庆401331)
1 引 言
数学分析中的微分中值定理是指Rolle,Lagrange,Cauchy三个微分中值定理.它们是数学分析中的基本内容.不同的教材处理这三个定理的方式也不尽相同.一般有两种方式:一种是按认识事物的过程来讲解,即先介绍Rolle中值定理,再利用它构造辅助函数来证明Lagrange中值定理,最后推广到Cauchy中值定理[1];另一种处理方式是先证明Rolle中值定理,然后统一地处理Lagrange中值定理和Cauchy中值定理[2].
关于微分中值定理的研究有很多方面, 主要涉及它的证明及其应用[4].例如,利用微分中值定理去判断函数的零点、函数的最值点、求函数的极限、证明一些特殊的不等式以及导数的估计等等.在证明或应用微分中值定理时,往往会提及中值定理的几何意义,一般不够深刻.本文将系统地阐述这三个中值定理背后所隐藏的几何背景,并不强调它们的证明或应用.几何上,我们将指出这三个定理本质上其实是一回事.
2 2合同变换
〈v,w〉∶=x1x2+y1y2,




O(2)={T是2×2矩阵|T·Tt=I2}.





3 2中曲线的相切
按照运动学的观点,平面上的曲线可以理解为一个质点在一段时间内在平面上运动的轨迹.数学上,平面上的曲线可以看成从开区间(a,b)到2的一个映射,即

下面我们给出曲线相切的定义,即



则称曲线γ1(t),γ2(t)在P点相切.

证设曲线
γ1(t)=(x1(t),y1(t)),γ2(t)=(x2(t),y2(t)),t∈(-ε,ε);



由已知条件并注意到P0是常值向量,可得
;

4 微分中值定理的几何观点
本节我们将利用前面的准备知识,从几何的角度去看这三个微分中值定理.
Rolle中值定理设f是[a,b]上的连续函数,在(a,b)内可导,且f(a)=f(b),那么存在一点ξ∈(a,b),使得f′(ξ)=0.

图1
如图1所示,Rolle中值定理的几何等价说法是:对于第一类可导曲线γ(x)=(x,f(x)),在定理的条件下,则存在γ(x)上的一点γ(ξ),ξ∈(a,b),以及一条直线lξ满足:
(i)lξ过点γ(ξ);
(ii)lξ的斜率k=0;
(iii)lξ与γ(x)相切于点γ(ξ).
Lagrange中值定理设f是[a,b]上的连续函数,在(a,b)内可导,那么存在一点ξ∈(a,b),使得


图2
类似于Rolle中值定理,如图2所示,Lagrange中值定理是说:对于端点不在水平直线上的第一类可导曲线γ(x),在定理的条件下,则存在γ(x)上的一点γ(ξ),ξ∈(a,b),以及一条直线lξ满足:
(i)lξ过点γ(ξ);

(iii)lξ与γ(x)相切于点γ(ξ).
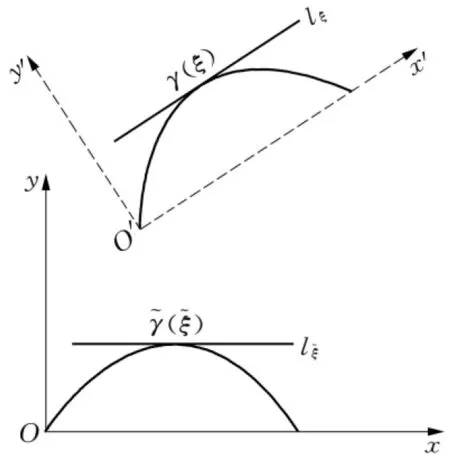
图3

Cauchy中值定理设f和g是[a,b]上的连续函数,在(a,b)内可导,且当x∈(a,b)时g′(x)≠0,那么存在一点ξ∈(a,b),使得
在Rolle和Lagrange中值定理的几何描述时,所遇到的曲线是第一类可导曲线.下面我们指出Cauchy中值定理事实上是Lagrange中值定理的第二类曲线版本.事实上,x∈(a,b)时g′(x)≠0,根据导数的介值性,我们可以假定当x∈(a,b)时g′(x)>0,即函数t=g(x)严格单调增.因此,函数t=g(x)可逆,记为x=g-1(t).因此,第二类曲线γ(x)=(g(x),f(x)),x∈(a,b),可以改写为第一类曲线:γ(t)=(t,F(t)),其中t∈(g(a),g(b)),F(t)=f(g-1(t)).
注意到,

从而对γ(t)运用Lagrange中值定理便得到Cauchy中值定理.
综上所述,我们可以说Rolle中值定理、Lagrange中值定理和Cauchy中值定理是欧氏几何学中曲线相切这一现象在不同坐标系中或在不同曲线的表示形式下的各种描述,其几何本质是相同的.
[参 考 文 献]
[1] 陈纪修,於崇华,金路.数学分析(上册)[M].北京:高等教育出版社,2004.
[2] 常庚哲,史济怀.数学分析教程(上册)[M].北京:高等教育出版社,2003.
[3] 彭家贵,陈卿.微分几何[M].北京:高等教育出版社,2002.
[4] 张庆娜.微分中值定理及其应用[D].安阳师范学院毕业论文,2010.
