永磁同步平面电动机的滑模控制器设计

王丽梅， 郑浩， 贾启

(1.沈阳工业大学电气工程学院，辽宁沈阳 110870;2华晨宝马汽车有限公司，辽宁沈阳 110044)

0 引言

许多传统的机械定位平台，多采用交叉轴型或龙门架型，由旋转电机配合传动机构驱动。而现代平面电机则是采用直线电机直接驱动的单层机械结构，按驱动用直线电机执行器的种类，可将平面电机划分为变磁阻型、感应型、永磁同步型3类，其中永磁同步平面电机在结构设计、控制精确度、推力密度、效率等方面具有明显优势，受到了学术界和工业界的广泛关注［1］。同采用旋转电机和直线电机叠加的传统XY平台相比，采用平面电动机构造XY工作台，具有直接驱动、结构简单、无传动机构、运动惯量小等特点，在现代制造装备中，具有很大的应用潜力。

目前，永磁同步平面电动机多基于4组永磁同步直线电机组合的方式实现，通过协调控制各个直线电机的电磁力来控制平面电机，以产生动子平移运动所需的X向推力、Y向推力及动子偏转所需的转矩。文献［2］研究了一种4组直线电机构成的平面电机，采用伪微分前馈控制实现三自由度的跟踪控制。文献［3］研究了一种4组直线电机构成的平面电机，采用基于状态方程的极点配置方法设计三自由度的位置伺服控制算法，达到预期动、静态指标。文献［4］研究了一种4组直线电机构成的平面电机，采用基于状态观测器的PID控制策略实现平面电机的定位控制。滑模控制对于由外界干扰等不确定因素造成的系统结构变化有很强的抑制作用［5－6］，干扰观测器对外部扰动估计并进行补偿［7］，应用在直线电机的位置控制中可以获得较高的控制精度和鲁棒性，但在平面电机上的应用还很少见［8－10］。

本文在合理假设的基础上分析了平面电机的动力学模型，建立了平面电机的运动控制模型，采用基于干扰观测器的二阶滑模控制方法进行位置控制器设计，利用饱和函数代替传统的切换函数，通过连续控制使滑模面及其时间导数在有限时间内趋近于零，削弱抖振的同时抑制不确定性因素对系统性能的影响，使平面电机定位精度达到高加工精度要求。

1 平面电机数学模型

由于动子在旋转中产生的偏转角对平面电机电磁特性的影响规律比较复杂，难以用简单的数学方法描述，所以假设动子偏转角很小，对各组直线电机电磁特性的影响忽略不计［3］。

1.1 平面电动机动力学分析

平面电机动子受4组直线电机推力的共同作用，作用点分别是每组永磁阵列的几何中点，动力学模型如图1所示。推力F1和F2与动子坐标系X0Y的X轴平行，推力F3和F4与动子坐标系X0Y的Y轴平行。动子采用气浮轴承，由于动子和定子之间没有直接接触，所以动子与定子之间的摩擦力可以忽略，根据经典力学原理可以得到动子的运动方程为

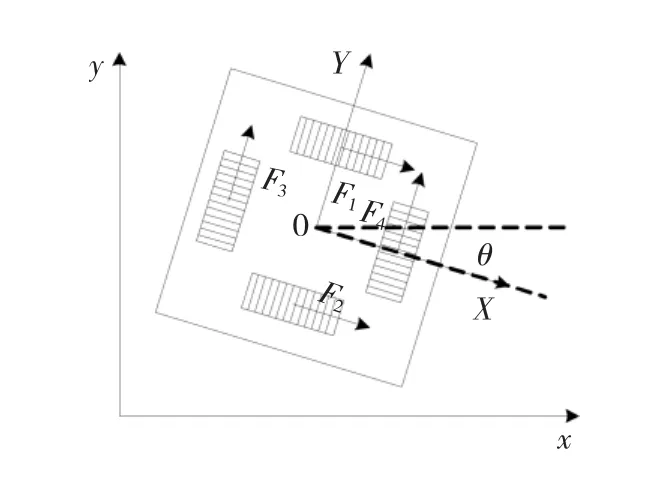
图1 动子受力分析Fig.1 The mover force analysis

其中:M和J分别为动子的质量和转动惯量;θ为动子绕Z轴的偏转角，d1、d2、d3、d4为各推力与相应平行坐标轴之间的距离。

1.2 永磁同步直线电机电磁力模型

假设永磁同步平面电机中所用永磁同步直线电机的性能均一样，由直线电机理论可知，永磁同步直线电机的电磁推力为

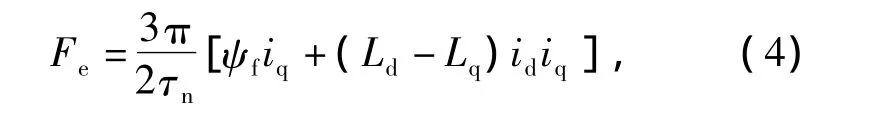
式中:id、iq、Ld、Lq分别为dq轴电流和电感;ψf为永磁体有效磁链;τn为极距。

为有效产生推力，采用id=0的矢量控制，则直线电机推力模型简化为

在利用动力学模型控制x、y、θZ方向运动时，电机推力、动子位置和执行器电流三者紧密相关，机电耦合过于复杂。为解决上述问题，在控制电机电流时无需考虑动子位置的微小变化，可以对3个自由度进行单独控制。

2 基于干扰观测器的滑模位置控制

永磁同步平面电机三自由度位置控制结构图如图2所示。

三自由度指令信号经过坐标变换得到4组直线电机的位置指令，位置控制器产生控制信号，各直线电机产生的电磁推力共同作用在永磁同步平面电机动子上，使动子向指定位置运动，完成平面电机的位置控制。

图2 位置伺服控制结构图Fig.2 Block diagram of position servo control

2.1 控制器组成结构

基于干扰观测器的滑模位置控制器由二阶滑模位置控制器和干扰观测器组成，如图3所示。图中Xr为位置参考输入，d为等效干扰，N、M为归一化的互质因子，ΔN、ΔM为系统不确定因素的归一化互质因子，X为位置输出，ζ为测量噪声，us为滑模控制器输出，u为控制输入，虚框内为干扰观测器部分，Q为低通滤波器，d^为干扰估计值。

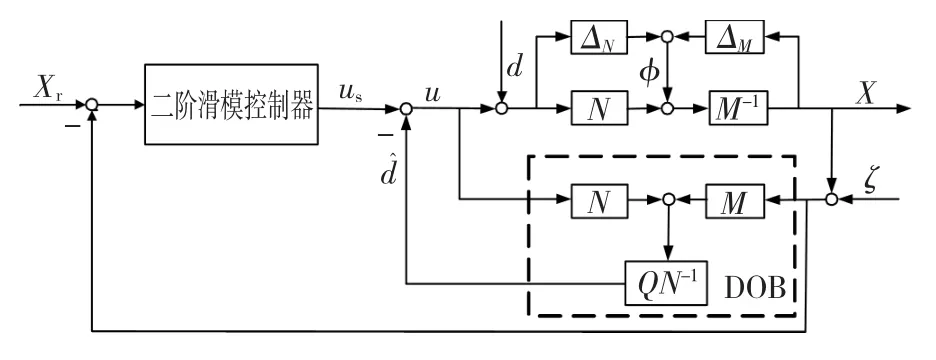
图3 控制器组成结构图Fig.3 Block diagram of the controller

2.2 干扰观测器设计

由框图可知，实际系统的传递函数为

系统的名义模型为

由图3可以求出系统输出对us、d、ζ和φ的传递函数为

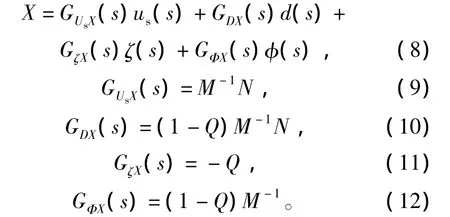
低通滤波器Q形式为

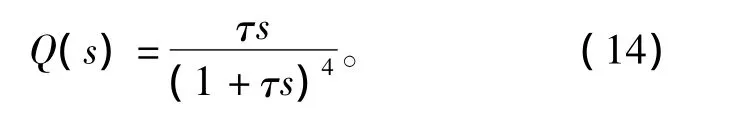
2.3 滑模控制器设计

令状态向量

x=［x1x2x3x4］T=［xvidiq］T，输入u=［u1u2］T=［uduq］T，则永磁同步直线电机的数学模型可表示为为二项式系数，m为分母阶数，n为分子阶数。低通滤波器选择有如下准则［11］:

准则1:随着低通滤波器Q的分子阶数增加，干扰抑制性能将得到提高，如果分子阶数相同，分母阶数越大干扰抑制性能越好;随着低通滤波器Q相对阶(m－n)增加，抑制测量误差的性能将提高，如果相对阶相同，分母阶数越小抑制测量性能越好。

准则2:滤波器时间常数越小干扰抑制性能越好。

准则3:采样时间T在低频范围内会影响干扰抑制效果。

综合考虑干扰抑制性能、系统对测量噪声的灵敏性和稳定性，取

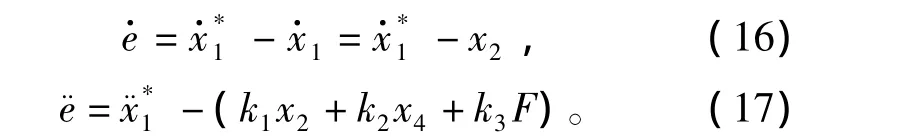
定义滑模面向量

其中，c1为正常数。滑模面的一阶和二阶导数分别为

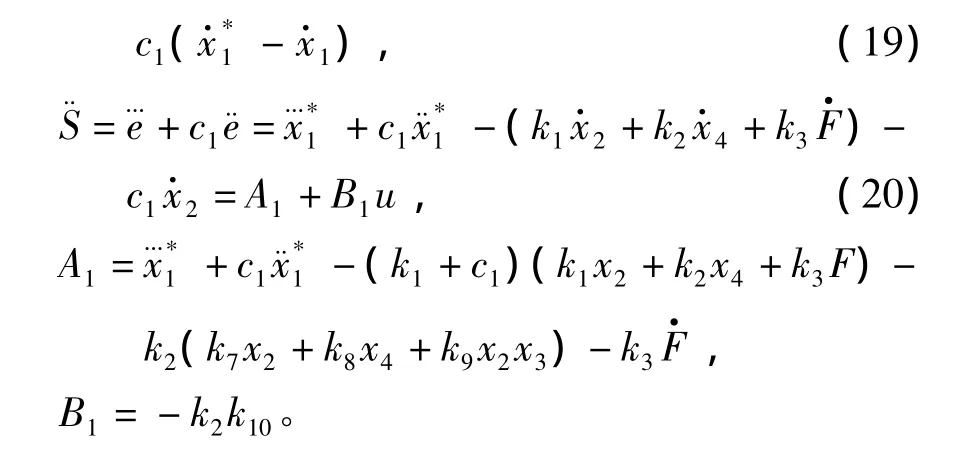
传统超螺旋算法仅适用于相对阶为1的系统，对于系统相对阶为2的情况，本文采用一种改进的超螺旋算法，设计控制器使状态轨迹在有限时间内螺旋式地收敛到原点，本文采用改进的超螺旋算法设计滑模控制器，此算法不需要计算滑模量导数及其符号信息，具有很强的鲁棒性，改进超螺旋算法的控制定义为

其中:sat(s)为饱和函数;λ、W、k、u0、Δ 都是正常数。有限时间内收敛到滑模面的充分条件为

其中，二阶滑模位置控制器如图4所示。

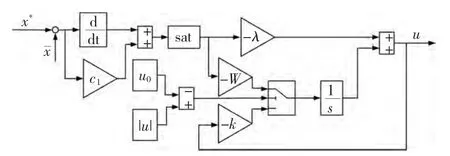
图4 二阶滑模位置控制器控制框图Fig.4 Block diagram of second order sliding model position controller

3 仿真结果及分析

本文针对永磁同步平面电机采用4组同型号直线电机进行研究，采用MATLAB7.1进行仿真，采样时间设定为0.000 1 s。电机参数为Rs=2.6 Ω，Ld=Lq=24.5 mH，τ=30 mm，kbemf=1.6 V·s/m，kf=1.6 N/A，p=3，M=2.8 kg。

经过多次实验后，根据式(18)、(24)选定滑模控制器的参数为c1=35，λ=25，k=4，W=1，u0=2，Δ=0.05;干扰观测器的参数τ=1 ms。

为了便于比较，对不加干扰观测器的滑模控制系统也进行了仿真，系统在0.25 s时外加最大推力20%的阶跃扰动，图5为两种控制方法对应的位置响应曲线。

由图5可以看出，与滑模控制器相比，基于干扰观测器设计的位置滑模控制器在突加扰动后系统响应超调较小，调整时间短，仍维持较高位置精度，具有很好的抑制作用，位置精度达到±0.1 μm，系统抗扰动能力较强，仿真结果表明基于干扰观测器的二阶滑模控制控制策略对于扰动具有较好的鲁棒性。

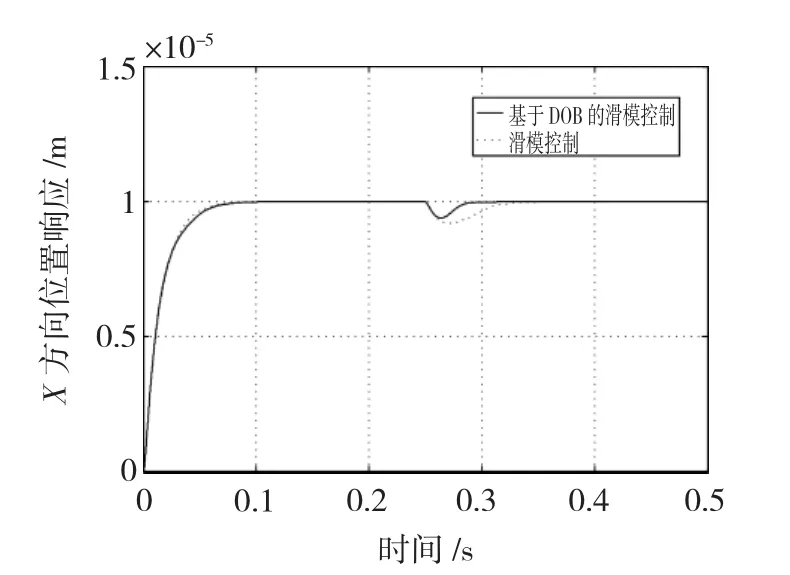
图5 平面电机X方向阶跃扰动下的响应曲线Fig.5 X direction step respond on the condition of step disturbance

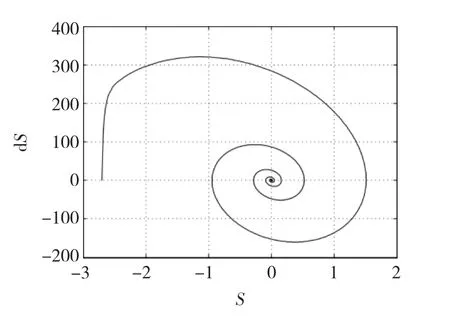
图6 滑模变量S相轨迹Fig.6 Phase trajectory of sliding mode variableS

系统引入外界干扰后进行各自由度定位仿真实验。X方向0.1 mm阶跃响应如图7所示，上升时间约为0.08 s，稳态误差平均值小于0.3 μm;Y方向最大受扰振幅为0.5 μm;θ方向最大受扰振幅为0.02 m·rad。

图7 X方向阶跃响应Fig.7 X direction step response

θ方向1 m·rad阶跃响应如图8所示，上升时间约为0.07 s，稳态误差平均值小于0.01 m·rad;X方向最大受扰振幅为0.48 μm;Y方向最大受扰振幅为0.5 μm。

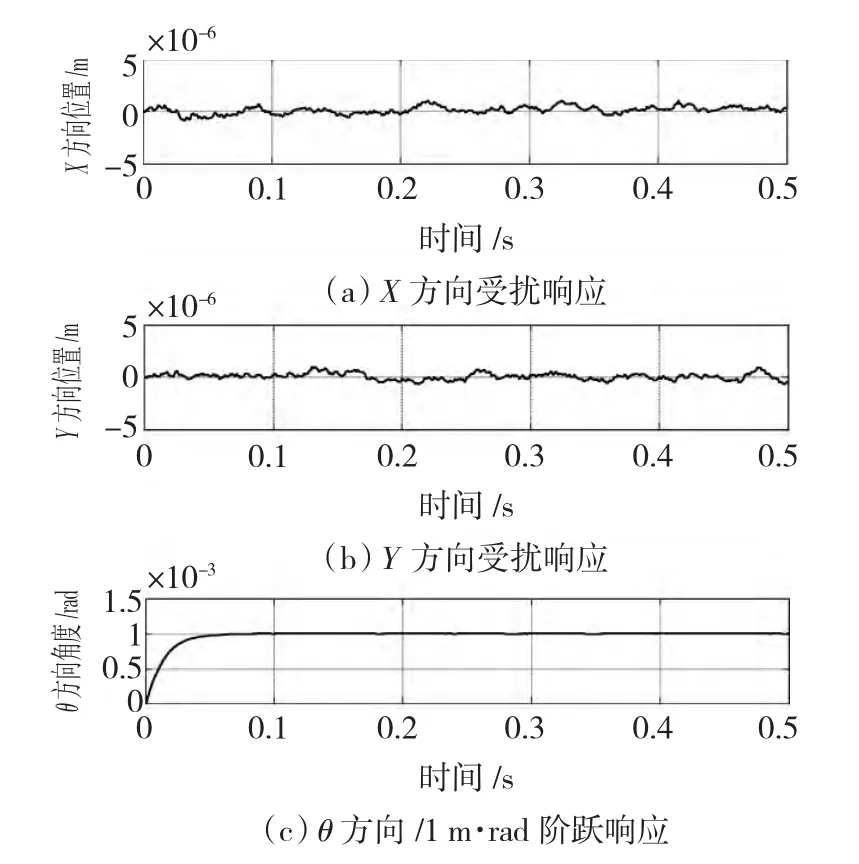
图8 θ方向阶跃响应Fig.8 θ direction step response

图9为平面电机三自由度同时定位响应曲线，X、Y方向0.1 mm阶跃给定指令，θ方向1 m·rad阶跃给定指令，X方向阶跃响应上升时间约为0.09 s，稳态误差平均值小于0.45 μm;Y方向阶跃响应上升时间约为0.08 s，稳态误差平均值小于0.8 μm;θ方向阶跃响应上升时间约为0.08 s，稳态误差平均值小于0.07 m·rad。比较图7和图8可以看出，进行三自由度同时定位控制，各个自由度的动态特性和稳态特性与单自由度定位控制时基本保持一致。

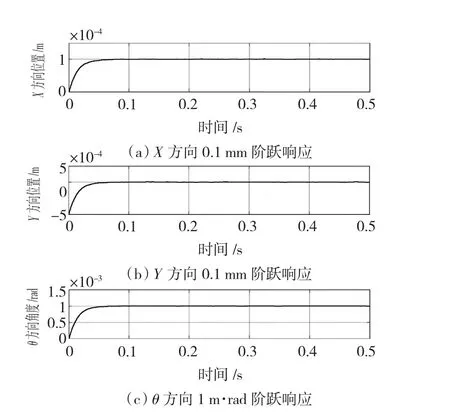
图9 三自由度定位响应Fig.9 The three degree of freedom position response

4 结语

本文针对永磁同步平面电动机的结构特点，提出了基于干扰观测器的滑模控制策略。设计了干扰观测器，对外部扰动进行补偿，设计了基于改进超螺旋算法的二阶滑模位置控制器，干扰观测器和滑模控制两者相互补充，提高了系统的抗干扰能力和鲁棒性。对系统进行单自由度定位和三自由度同时定位仿真实验，仿真结果表明所采用的控制策略和控制算法使系统获得较好的定位精度，同时具有良好的鲁棒性和稳定性。

［1］周赣，黄学良.三自由度永磁同步平面电机的控制策略［J］.电机与控制学报，2011，15(4):41－45.

ZHOU Gan，HUANG Xueliang.Control strategies of 3-degree-offreedom synchronous permanent－magnet planar motors［J］.Electric Machines and Control，2011，15(4):41－45.

［2］YEN J Y，KUO F T，LEE M C，et al，Planar motion stage control using PDFF controller［C］//Proceeding of the 2011 9th World Congress on Intelligent Control and Automation，June 21－25，2011，Taipei，China.2011:749－752.

［3］曹家勇，朱煜，汪劲松.永磁同步平面电动机三自由度运动控制器［J］.中国电机工程学报，2006，26(17):143－147.

CAO Jiayong，ZHU Yu，WANG Jingsong.A three degree of freedom motion controller for synchronous permanent magnet planar motors［J］.Proceedings of the CSEE，2006，26(17):143－147.

［4］DEJIMA Shuichi，GAO Wei，KATAKURA Kei，et al.Dynamic modeling controller design and experimental validation of a planar motion stage for precision positioning［J］.Precision Engineering，2005，29(3):263－271.

［5］刘金琨.滑模变结构控制MATLAB仿真［M］.北京:清华大学出版社，2005:4－6.

LIU Jinkun.MATLAB Simulation for Sliding Mode Control［M］.Beijing:Tsinghua University Press，2005:4－6.

［6］贾洪平，贺益康.永磁同步电机滑模变结构直接转矩控制［J］.电工技术学报，2006，21(1):1－6.

JIA Hongping，HE Yikang.Variable structure sliding mode control for PMSM DTC［J］.Transactions of China Electrotechnical Society，2006，21(1):1－6.

［7］张代林，陈幼平，艾武，等.基于观测器模型的直线电机干扰抑制技术的研究［J］.中国电机工程学报，2007，27(12):14－18.

ZHANG Dailin，CHEN Youping，AI Wu，et al.Research on disturbance suppression technology for linear motors based on a disturbance observer Model［J］.Proceedings of the CSEE，2007，27(12):14－18.

［8］孙宜标，郭庆鼎.基于推力观测器的直线式交流伺服系统滑模变结构控制［J］.电工技术学报，1998，13(2):1－5.

SUN Yibiao，GUO Qingding.Thrust observer-based sliding mode variable structure control for linear AC servo system［J］.Transactions of China Electrotechnical Society，1998，13(2):1－5.

［9］孙宜标，杨雪，夏加宽.采用鲁棒微分器的永磁直线同步电机二阶滑模控制［J］.中国电机工程学报，2007，27(33):6－10.

SUN Yibiao，YANG Xue，XIA Jiakuan.Second order sliding mode control for PMLSM using robust differentiator［J］.Proceedings of the CSEE，2007，27(33):6－10.

［10］张前，黄学良，周赣.永磁同步直线电动机的位置滑模控制器设计［J］.微特电机，2010，38(5):53－55.

ZHANG Qian，HUANG Xueliang，ZHOU Gan.Design of position servo controller based on sliding mode control for permanent magnet linear synchronous motors［J］.Small＆Special Electrical Machines，2010，38(5):53－55.

［11］YANG Kwangjin，CHOI Youngjin，CHUNG Wankyun，Performance analysis of discrete-time disturbance observer for second order systems［C］//Proceedings of the 42nd IEEE Conference on Decision and Control，December 9－12，2003，Maui，USA.2003，5:4877－4882.