双Y移30°PMSM两电机串联系统的谐波效应
2014-09-20刘陵顺张少一刘华菘
刘陵顺, 张少一, 刘华菘
(海军航空工程学院控制工程系,山东烟台 264001)
0 引言
全电舰船、多电飞机概念的提出,以及机车牵引、机器人、纺织、造纸等工业用电系统的应用要求,需要研究解耦运行的多电机交流传动系统,为此提出了一种基于广义零序谐波分量的单逆变器驱动双Y移30°PMSM两电机串联系统。该系统是由两台双Y移30°PMSM按照一定的定子绕组联结规则串联而成,可在同一逆变器和同一套控制平台下实现各台电机的解耦运行,有助于节省控制驱动装置及其外围电路,降低了系统的体积、重量与成本。目前对于单逆变器驱动多电机串联系统的研究多以原理可行性探索为主,研究对象主要集中在多相感应电动机串联系统,对于多相PMSM串联系统的研究还较为少见[1],已有文献主要研究了理想正弦波磁场分布下多电机串联系统的基本原理和控制策略[2-5]。由于电机的实际气隙磁场通常存在着一系列的高次谐波,将对串联系统的解耦控制产生影响。为此,文献[6]采用虚拟多电机机电耦合的概念就五相PMSM反电动势谐波对串联系统矢量控制的影响进行了分析,文献[7]分别研究了2台五相电机串联系统以及对称六相串联三相电机系统的定子绕组设计特点。考虑到双Y移电机可靠性更强,其力矩脉动平均值只有对称六相电机的14%,谐波电流较小,双Y移30°PMSM两电机串联系统具有更大的军事应用价值。本文以定子集中绕组的双Y移30°PMSM为研究对象,利用绕组函数的概念,研究了不同类别的高次空间谐波与另一台相串联的双Y移30°PMSM基波磁动势相互作用对系统解耦运行产生的影响规律,建立了该串联系统中其中一台PMSM包含5、7次空间谐波的多维空间数学模型,进行了变速、变负载的仿真研究,揭示了该串联系统多相PMSM定子绕组必须为正弦波分布的根本原因。
1 高次空间谐波的耦合效应分析
正弦波分布的双Y移30°PMSM基于自然坐标系下的数学模型经过全维空间解耦矩阵运算后,变换到由dq-xy-o1o23个正交基组成的正交平面上,其中电机的电磁转矩完全是由dq电流分量决定,而与它们的xy电流分量和o1o2零序分量无关[8-12]。因此,双Y移30°PMSM的磁通和转矩控制只需要dq平面上的两个电流分量即可,而xy平面的2个电流分量可以用来控制另一台双Y移30°PMSM,为此需将另一台电机的定子绕组与第一台电机的定子绕组通过适当的相序转换串联在一起,保证第一台电机的磁通和转矩生成电流分量不会在在第二台电机中生成磁通和转矩,反之亦然。2台双Y移30°PMSM串联系统与逆变器的联结图如图1所示。
为了分析图1串联PMSM定子绕组必须为正弦分布,下面利用PMSM1含有所有谐波的集中绕组研究各类谐波对解耦运行的影响情况,假设定子绕组分布不对称,则PMSM1中的高次谐波主要有:12i±1次(i=1,2,3,…)以及6i±1次(i=1,3,5,…)两大类奇次谐波以及各偶次谐波。
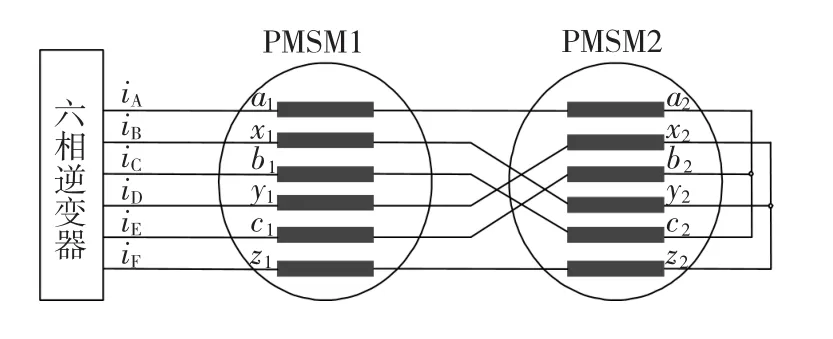
图1 两台双Y移30°PMSM串联系统Fig.1 Dual Y shift 30°PMSM series-connected system
根据图1中的联结关系,假设两台电机的基波电流的初始相位为零,则可得逆变器输出电流与2
台串联电机电流的关系为[7]
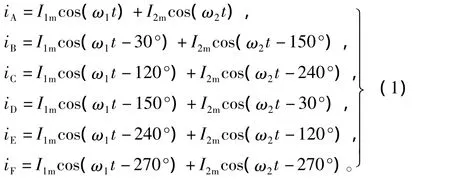
其中,I1m,I2m分别为2台电机基波电流分量的幅值,ω1,ω2分别为2台电机基波电流分量的角频率。
假定PMSM1短距集中绕组下a相的绕组函数如图2所示。

图2 短距集中绕组下a相的绕组函数波形Fig.2 Winding function waveform of short-pitched concentrated coil

设PMSM1每相绕组的总有效匝数为Ns1,δ为短距角度,各相绕组函数之间的关系为
所以PMSM1定子绕组的傅里叶函数推导为

利用式(1)中PMSM2的磁通、转矩基波电流以及式(3),可得PMSM1中的第j次谐波与PMSM2基波电流产生的磁动势表达式为

据此可以推导出PMSM1气隙磁场中各类谐波与PMSM2的耦合作用,具体讨论如下:

据此,PMSM1的(6i±4)次谐波(i=1,3,5,…)与PMSM2的基波电流耦合在PMSM1内产生旋转磁场。(6i+4)次谐波产生的旋转磁场转向与PMSM2的基波磁场相反,(6i-4)次谐波产生的旋转磁场转向与PMSM2的基波磁场相同。

据此,PMSM1的(6i±2)次谐波(i=1,3,5,…),与PMSM2的基波电流耦合在PMSM1内产生旋转磁场。(6i+2)次谐波产生的旋转磁场转向与PMSM2基波磁场相同。(6i-2)次谐波产生的旋转磁场转向与PMSM2基波磁场相反。
同理,对于PMSM1中的奇次谐波与PMSM2的

其中,i=1,3,5,…。
(6i±1)次谐波(i=1,3,5,…)与PMSM2的基波电流耦合在PMSM1内产生旋转磁场。其中(6i+1)次谐波产生的旋转磁场转向与PMSM2的基波磁场相反,(6i-1)次谐波产生的旋转磁场转向与PMSM2基波磁场相同。
此外,(12i±1)次奇次谐波(1,11,13,23,25…)以及3的倍数次谐波,将不会与PMSM2的基波电流产生耦合,因而,其产生的旋转磁动势为零。
由此可见,PMSM2的基波电流与PMSM1的某些高次谐波互相耦合,在PMSM1中产生旋转磁动势,其旋转速度由两台串联电机的同步转速ω1和ω2共同控制,通常情况下 ω2与 ω1不相等,会在PMSM1中产生电磁转矩脉动,从而影响PMSM1的正常运行。因此,在该串联系统中,务必要求两台串联电机的磁场分布呈正弦波,且在空间对称分布,从而消除各偶次谐波以及(6i±1)次奇次谐波,i=1,3,5,…。
另外,尽管PMSM1中的(12i±1)次谐波不与PMSM2的基波电流耦合产生旋转磁动势,但它们会与自身的基波电流分量作用产生高次转矩纹波,因此,在电机设计中需要消除这些谐波。基波电流相互耦合的效果分析如下:
25 、7次空间谐波对解耦控制的影响仿真
2.1 含5、7次谐波的串联系统数学模型
通常电机的定子绕组呈对称分布,偶次谐波自然消失。为了验证串联电机的(6i±1)奇次谐波(i=1,3,5,…),对该串联系统运行存在的耦合问题,假定PMSM1中包含5、7次谐波(其他更高次谐波由于幅值过小可忽略),PMSM2中气隙磁场只有基波,不存在高次谐波。
设Ns1Ns1为PMSM1的每相定子绕组匝数,φfm1φfm1为PMSM1永磁主磁通,θr1为PMSM1转子磁场轴线与定子A相绕组轴线之间的电角度,φfm1-5为PMSM1的5次谐波磁通,φfm1-7为PMSM1的7次谐波磁通,Ns1-5为PMSM1的5次谐波等效绕组匝数,Ns1-7为PMSM1的7次谐波等效绕组匝数,Ns2为PMSM2的定子绕组匝数,φfm2为PMSM2永磁主磁通,θr2为PMSM2转子磁场轴线与定子A相绕组轴线之间的电角度。
PMSM1的转子磁场与定子绕组交链的磁链为

PMSM2转子磁场交链在定子各相绕组中的磁链为
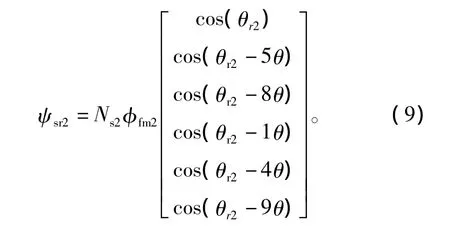
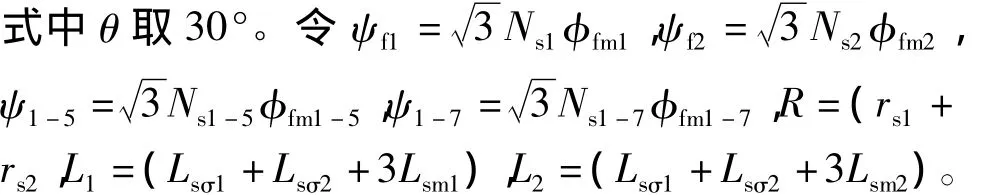
经同步旋转坐标变换后,可推出PMSM1和PMSM2电压方程为


图3 串联系统基于id=0的矢量控制系统图Fig.3 Vector control system based on id=0 for series-connected system

PMSM1和PMSM2的转矩方程分别为
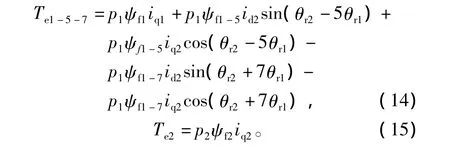
分析式(14)、式(15)可见,在PMSM2的id2或iq2id2非零时,PMSM1的电磁转矩必有脉动,脉动幅值主要与id2、iq2以及空间谐波 ψ1-5、ψ1-7的大小相关,脉动的频率和2台电机的转速都相关。PMSM2的转矩只与自身的iq2和ψf2有关,不受PMSM1的空间谐波影响。
2.2 PMSM1含5、7次谐波串联系统耦合性能仿真
为了验证PMSM1含有的5、7次空间谐波会影响串联系统的解耦控制,采用id=0的载波调制
PWM矢量控制策略对2台双Y移30°PMSM串联系统建模仿真,如图3所示。参数设置:极数p1=p2=4,磁通 ψf1=ψf2=0.2 Wb,ψ1-5=0.08 Wb,ψ1-7=0.06 Wb,摩擦系数B1=B2=0.05,转动惯量J1=J2=0.1 kg·m2,R1=R2=2.875 Ω,L1=L2=0.12 H。
PMSM1变负载仿真如图4所示:PMSM1含5、7次空间谐波,初始负载为1 N·m,在1 s从1 N·m增加到10 N·m,转速为200 r/min;PMSM2不含谐波,负载为2 N·m不变,转速为250 r/min。
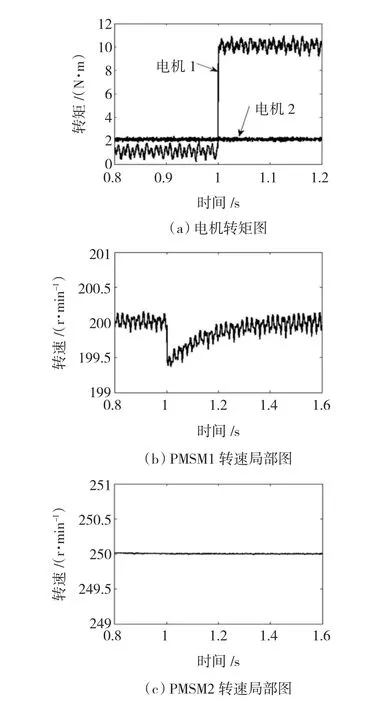
图4 PMSM1变负载运行Fig.4 Variable load operating of PMSM1
由以上仿真可知:
1)当PMSM1含5、7次空间谐波,PMSM2只有基波时,只要PMSM2带负载,即iq2存在,PMSM1就存在转矩和转速脉动,脉动的频率和幅值与PMSM1的负载变化无关。
2)PMSM1的负载增加对PMSM2的转速和转矩均无影响,这说明不含空间谐波的PMSM2在该串联系统中不受PMSM1的变载影响。
3)PMSM1的负载在1 s增加时,其转速小幅下降并迅速恢复。
PMSM2变负载仿真如图5所示:PMSM1含5、7次空间谐波,空载不变,转速设为200 r/min;PMSM2不含谐波,负载为2 N·m,在1 s时从2 N·m变为10 N·m,转速设为250 r/min。
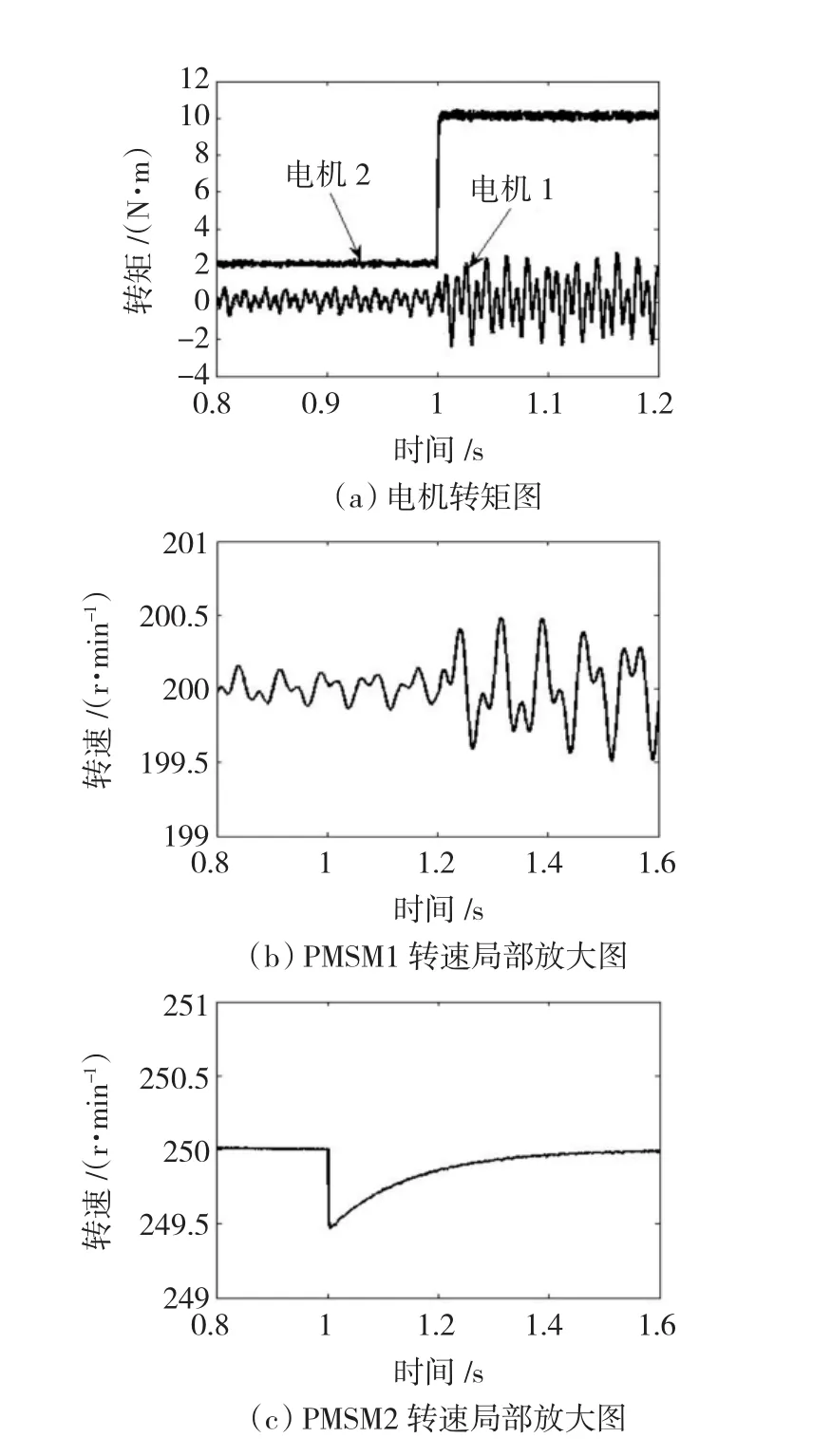
图5 PMSM2变负载运行Fig.5 Variable load operating of PMSM2
1)PMSM2的负载增大后,PMSM1的转矩和转速脉动幅值都增大,即PMSM1的转矩和转速脉动幅值受PMSM2的负载影响,脉动频率与PMSM2的负载大小无关。
2)PMSM2在1s负载增加后转速小幅下降,并迅速恢复。且不含谐波的PMSM2负载变化时,其自身的转矩和转速不存在任何脉动。
PMSM1变速仿真如图6所示:PMSM1含5、7次空间谐波,且空载运行,初始给定为200 r/min,在0.9 s从200 r/min加速到350 r/min;PMSM2不含谐波,其负载为2 N·m,给定转速为250 r/min。
1)PMSM1的转速增加对PMSM2的转速、转矩均无影响,这说明不含空间谐波的PMSM2在该串联系统中不受PMSM1的变速影响。
2)比较PMSM1变速前后的转速图,PMSM1的转速增加使其转速脉动的频率有所升高。
PMSM2变速仿真如图7所示:PMSM1含5、7次空间谐波,且空载运行,给定转速为200 r/min;PMSM2不含谐波,其负载为2 N·m,在0.9 s从100 r/min加速到400 r/min。
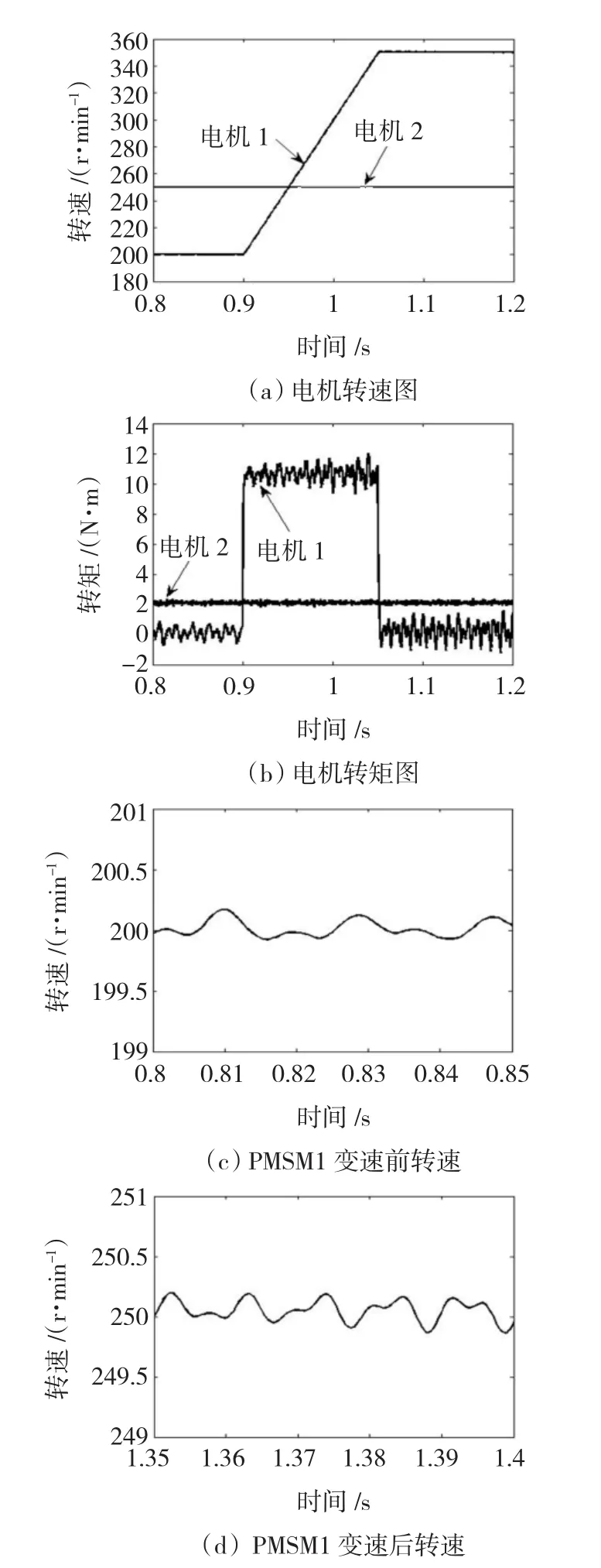
图6 PMSM1变速运行Fig.6 Variable speed operating of PMSM1
在PMSM2的转速增加过程中,PMSM1的转矩脉动幅值和频率均有所增大。但PMSM2的转速和转矩均不存在脉动。
从以上仿真可以得出结论:
1)含5、7次空间谐波的PMSM1转矩脉动与PMSM2的负载大小有关,脉动频率与PMSM1以及PMSM2的转速都相关,因此该串联系统中PMSM1的运行是不解耦的。
2)若PMSM2不含空间谐波,其运行不受PMSM1变载变速的影响。因此,若实现该串联系统中2台电机的解耦运行,每台电机均不能包含(6i±1)奇次谐波(i=1,3,5,…)。
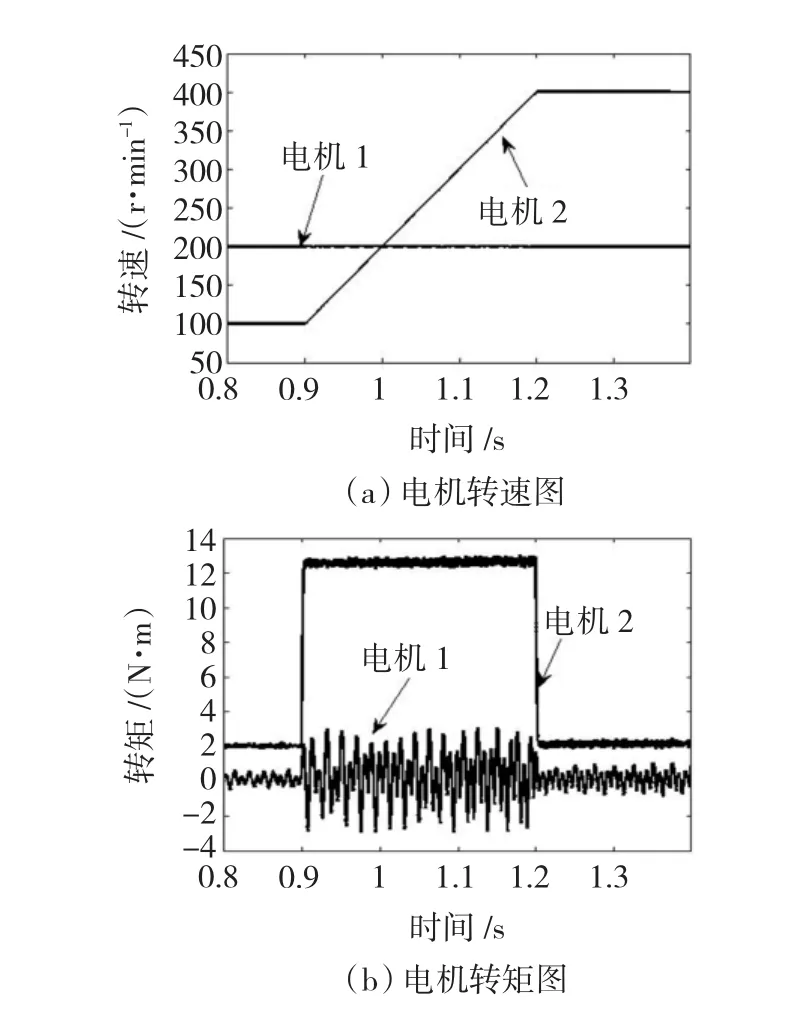
图7 PMSM2变速运行Fig.7 Variable speed operating of PMSM2
3 结语
为了分析电机高次空间谐波对串联系统解耦运行的影响规律,本文建立了双Y移30°六相PMSM集中绕组函数的傅里叶变换式,利用PMSM1高次谐波与PMSM2基波电流耦合的磁动势关系式,分析了不同类别的高次谐波对串联系统解耦运行的影响规律,建立了该串联系统的数学模型并进行了变速、变负载仿真,提出了串联系统多相PMSM定子绕组必须为正弦波分布的必然要求,为电机的优化设计及空间谐波补偿的解耦控制提供理论基础。
[1]LEVI E.Multiphase electric machines for variable-speed applications[J].IEEE Transactions on Industrial Electronics,2008,55(5):1893-1909.
[2]LEVI E,JONES M.A novel concept of a multiphase multimotor vector controlled drive system supplied from a single voltage source inverter[J].IEEE Transactions on Power Electronics,2004,19(2):320-335.
[3]LEVI E,JONES M,VUKOSAVIC S N,et al.Operating principles of a novel multiphase multimotor vector-controlled drive[J].IEEE Transactions on Energy Conversion,2004,19(3):508-517.
[4]IQBAL A,LEVI E.Space vector PWM for a five-phase VSI supplying two five-phase series-connected machines[C]//12th International Power Electronics and Motion Control Conference,August 30-September 1,2006,Portoroz,Slovenia.2006:222-227.
[5]LEVI E.Even-phase multi-motor vector controlled driver with single inverter supply and series connection of stator windings[J].IEE Proceedings-Electric Power Applications,2003,150(5):580-591.
[6]SEMAIL E,LEVI E,BOUSCAYROL A,et al.Multi-machine modeling of two series connected 5-phase synchronous machines:effect of harmonics on control[C]//European Conference on Power Electronics and Applications,September 11-14,2005,Dresden,Germany.2005:1-10.
[7]LEVI E,JONES M,VUKOSAVIC S N,et al.Stator winding design for multi-phase two-motor drives with single VSI supply[C]//International Conference on Electrical Machines,September 2-5,2006,Chania,Greece.2006:CD-ROM Paper No.OMM2-1.
[8]艾永乐,王玉梅,KAMPER Marrten.梯形波相电流控制的六相感应电机建模与控制[J].电机与控制学报,2012,16(3):71-76.
AI Yongle,WANG Yumei,KAMPER Marrten.Modeling and controlling of six-phase induction machine driven trapezoidal phase current waveform[J].Electric Machines and Control,2012,16(3):71-76.
[9]彭兵,王成元,夏加宽.六相永磁力矩伺服电机气隙磁场优化[J].电机与控制学报,2011,15(12):39-42.
PENG Bing,WANG Chengyuan,XIA Jiakuan.Air-gap magnetic field optimization for six-phase permanent magnet torque servo motor[J].Electric Machines and Control,2011,15(12):39-42.
[10]杨金波,杨贵杰,李铁才.双三相永磁同步电机的建模与矢量控制[J].电机与控制学报,2010,14(6):1-7.
YANG Jinbo,YANG Guijie,LI Tiecai,Modeling and vector control for dual three-phase PMSM[J].Electric Machines and Control,2010,14(6):1-7.
[11]欧阳红林,成兰仙.多相永磁同步电机模糊神经网络控制调速系统[J].电机与控制学报,2007,11(2):111-115.
OUYANG Honglin,CHENG Lanxian.Multiple phase permanent magnet synchronous motor speed control system based on fuzzy neural network control[J].Electric Machines and Control,2007,11(2):111-115.
[12]赵品志,杨贵杰,李勇.三次谐波注入式五相永磁同步电机转矩密度优化[J].中国电机工程学报,2010,30(33):71-77.
ZHAO Pinzhi,YANG Guijie,LI Yong.Torque density optimization for five-phase PMSM with third harmonic injection[J].Proceedings of the CSEE,2010,30(33):71-77.
