直线感应电机空载速度特性分析

司纪凯， 艾立旺， 韩俊波， 许孝卓， 上官璇峰

(河南理工大学电气工程与自动化学院，河南焦作 454000)

0 引言

弧形直线电机和直线感应电机结构简单，其初级铁心和绕组端部直接暴露在空气中，同时次级很长，具有很大的散热面积，热量很容易散发掉，所以这一类直线电机的热负荷可以很高;并且产生直线运动不需要传动机构，有广泛的工业应用领域。直线感应电机与旋转异步电机原理基本相同，但是性能指标差别较大，这与直线电机结构的特殊性有关——初级有限长。所以大多数研究人员重点研究了直线感应电机初级有限长引起的纵向端部效应对其主要性能参数的影响。

文献［1－4］利用麦克斯韦方程组建立电机的数学模型并分析考虑端部效应影响在内的电机的推力;文献［5－7］重点分析了纵向端部效应和横向端部效应的作用机理，详细推导了这两种端部效应下直线感应电机的气隙磁场，推力、法向力、效率和功率因数的详尽表达式，并利用Matlab软件进行仿真验证。文献［8－10］分别基于感应电势中端部效应波感应电势分量、推力中端部效应力分量和直线电机的结构参数提出了考虑纵向端部效应的修正系数。鲜有少数研究关于纵向端部效应对电机空载运行速度或同步速度的影响:文献［11－12］提出考虑纵向端部效应时，需要在电机两个端部各附加上一段考虑端部散漏磁通的等效漏磁区域长度。文献［13－15］提出了在低速电机中可能出现端部效应波半波长大于极距的情况即端部效应波的平移速度大于同步平移速度，此时纵向端部效应力作为正向作用力叠加在推力上，但未对空载运行速度和同步速度做详细的研究。

本文主要针对仿真实验时发现的特殊现象－空载速度超过所谓的同步速度，利用Maxwell方程组建立单边直线感应电机的数学模型进行考虑纵向端部效应影响的磁场分析计算，并采用有限元法(finite element method，FEM)仿真进行验证。

1 问题的提出

直线弧形感应电机(相当于只具有一半定子的常规实心转子感应电机)的定子内、外径、轴径分别为155 mm、98 mm、30 mm，转子外径依气隙厚度而定;极数为4、槽数为12、相电压为110 V。建立直线弧形感应电机的有限元模型如图1所示。

当气隙厚度以0.5 mm为间隔从0.5 mm到5 mm变化时，分别建立有限元参数化模型，经过仿真得到其空载转速变化情况如图2所示。在一定范围内，该电机的空载转速随着气隙厚度的增加而逐渐增加，甚至在气隙厚度为2.5 mm时开始出现特殊的现象:电机在电动运行状态下的空载转速超过了理想同步转速(4 500(°)/s即750 r/min)。

图1 直线弧形感应电机有限元模型Fig.1 Finite element model of linear arc-shaped induction motor

图2 直线弧形感应电机空载转速与气隙厚度的关系Fig.2 Corresponding no-load speed of different air gap thickness in linear arc-shaped induction motor

图3 单边直线感应电机空载平移速度与气隙厚度的关系Fig.3 Corresponding no-load speed of different air gap thickness in SLIM

2 建模和分析

图4为弧形直线感应电机模型的瞬态磁通分布图。可以看到由于定子铁心的开断造成铁心端部存在着一定数量的散漏磁通。相对于一个完整实心转子异步电动机而言，定子铁心开断在一定程度上会使漏磁通穿出铁心向外延伸再闭合，这样就产生了考虑漏磁通影响的等效纵向端部漏磁区域长度。所以，铁心开断的单边直线感应电机的纵向端部效应对电机的性能影响必须给与慎重的考虑。

至于横向端部效应主要是因为初级和次级的宽度有限长造成的。横向端部效应的特殊表现为:气隙磁通沿直线电机横向呈不规则分布，具体表现为边缘处的气隙磁通密度增加，中间处的气隙磁通密度减少，整体呈马鞍形状分布。横向端部效应导致的直接结果是损耗的增加，较好的计入方法是修正次级导电率和阻抗，故本文不考虑横向端部效应。

图4直线弧形感应电机的瞬态磁通分布图Fig.4 Distribution of flux lines in linear arc-shaped induction motor

分析直线弧形感应电机和单边直线感应电机的结构特征以及它们的特殊现象——空载运行速度超过所谓的同步运行速度，可以发现它们具有一个很重要的共同特征:定子铁心开断。由于铁心开断引起的端部效应对电机的性能影响应当引起慎重考虑(尤其是动态纵向端部效应)，我们可以借助对如图5所示单边直线感应电机(铜次级)电磁场量的计算来分析动态纵向端部效应对其理想空载平移速度的影响来分析铁心开断对电机同步运行速度的影响。

图5 单边直线感应电动机的物理模型Fig.5 Physical model of SLIM

为保证一定精确度，对单边直线感应电动机的物理模型作一些理想化的假定如下:

1)磁场是沿着电机初级运动方向x轴变化的，与其他方向无关;

2)各种场量在空间和时间上作正弦规律变化的;

3)初级铁心的磁导率很大，其饱和影响可以忽略不计，磁滞损耗和集肤效应均忽略不计;

4)所考虑的电流方向都是在z轴方向的;

5)认为初级是光滑的，以便用只有宽度没有厚度的电流层表示电机的初级电流。因为励磁电流是正弦变化的，所以其产生的对应的场量在时间和空间上也是正弦变化的。

根据文献［16］由Maxwell方程组并根据所假设的单边直线感应电机物理模型列写下列方程为

式中:j1，j2分别为初级和次级电流线密度且j1=J1ej(ωt－ax)，A3z为矢量磁位的z轴分量且A3z=A3z(x，t)=Azejωt。联立边界条件求解得

图6为该电机在实际长度2pτ和两个端部一定范围内(约一个极距39.27 mm)瞬态气隙磁密竖直分量随距离x不同而变化的情况。

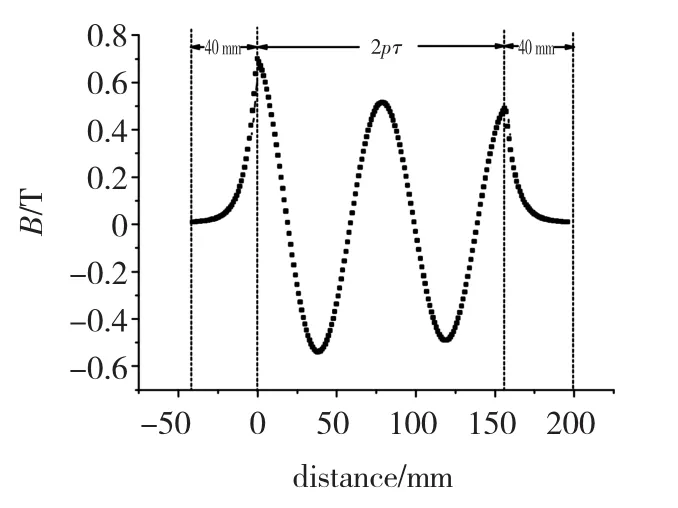
图6 瞬态气隙磁通密度分布图Fig.6 Distribution of air-gap magnetic flux density

由气隙磁通密度的变化情况可知在磁通密度在电机两个端部外一定范围内呈指数规律迅速衰减为零。为了满足磁通连续性原理，初级有限长即铁心开断在一定程度上会产生考虑纵向端部漏磁的等效漏磁区域长度附加在铁心长度上。设等效漏磁区域长度延长至端部磁通密度为0.368Bav处，则两个端部的等效外延尺寸d约为7 mm，相对于初级、次级无限长的情况而言，这样就导致初级绕组电流形成磁场的电磁极距大于电机本身的机械极距，这在电机端部两极表现的更为明显。因此，为了研究铁心开断对直线感应电动机同步速度的影响，提出一个新的物理概念——等效电磁极距τE，等效电磁极距为在一定极数下考虑电机的等效外延尺寸，电机的等效总长度除以极数而得的平均极距。由相对应于机械极距τ的修正系数k来计及不同极数情况下纵向动态端部效应对单边直线感应电机理想空载平移速度的影响。

在直线感应电动机中，端部效应随着极数的增加而减小。这是因为，极数较多时有助于分担恒定的端部效应影响，致使电机性能较好。则在同样条件下，不同极数的电机的k值不同，有

式中:d为考虑端部漏磁影响电机纵向的等效外延尺寸;p为极对数;τ为机械极距。

表1为电机在不同极数下k计算值。将数据进行曲线拟合得

表1 不同极数下的k的计算值Table 1 Corresponding k of different number of poles in analytical method

3 有限元仿真实验

图7为不同气隙厚度时气隙磁通密度随距离x变化的情况。可以看出:在0～2pτ范围内磁通密度幅值随着气隙厚度的增加呈现减少的趋势;在两个端部的一定范围内，磁通密度幅值随着气隙厚度的增加却呈现增加的趋势。众所周知，随着气隙厚度的增加，定、转子磁场之间的耦合度下降，相应的会使铁心开断的端部漏磁量增加。这样就使等效电磁极距变大以及相应的理想空载平移速度变大，本文对于气隙厚度与理想空载平移速度的关系只做定性的研究，重点研究极数与理想空载平移速度的关系。

图7 不同气隙厚度时的磁通密度分布Fig.7 Corresponding distribution of flux density of different air gap thickness

为对第2部分解析法的结果进行验证，在保持极距、槽形、气隙厚度等参数保持不变的情况下，当极数由3到10变化时，分别建立相应的有限元模型。图8为2p=4时的有限元模型以及相应的瞬态磁通分布图，可以看到由于初级铁心的开断造成铁心端部存在着一定数量的散漏磁通。

图82 p=4时的有限元模型以及相应的瞬态磁通分布Fig.8 (2p=4)finite element model of SLIM and corresponding distribution of flux lines

下面主要验证单边直线感应电机在不同极数下，动态纵向端部效应对电机空载平移速度的影响。图9为单边直线感应电机的空载平移速度随着极数增加时的变化情况，可见:随着极数的增加，空载平移速度越来越接近理想同步平移速度，但只是无穷接近于理想同步平移速度(3.927 m/s)。

图9 单边直线感应电机空载速度随极数增加的变化情况Fig.9 Corresponding no-load speed of different number of poles in SLIM

式中:τE，VE0为等效电磁极距，以及相应的空载平移速度;τ，VS为机械极距，以及相应的同步平移速度;f为电源频率。

表2为电机在不同极数情况下对应的k值。将数据进行曲线拟合，得

表2 不同极数下的k的仿真值Table 2 Corresponding k of different number of poles in simulation

图10 为修正系数k值解析解与有限元解图像的对比。可见:对于修正系数k的计算，有限元仿真计算k对应接近实际情况下电机的空载运行速度，解析法计算的k值由等效电磁极距得到，对应于电机的理想同步运行速度。有限元仿真计算结果对解析法计算结果趋势基本符合，并且前者低于后者3%～4%，即感应电机在电动状态下的空载运行速度接近同步速度但低于同步速度。

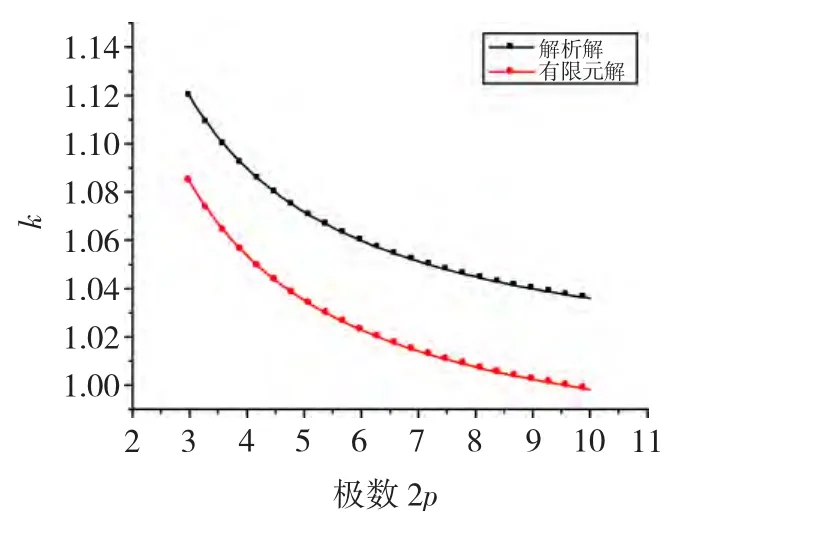
图10 修正系数k值解析解与有限元解的比较Fig.10 Comparison of calculation results of factor k by finite element method and analytical method

4 实验结果及分析

为了验证前文对空载运行速度超过所谓同步速度的理论分析的正确性，对图11所示样机进行实验测试。样机参数为:功率2 200 W、相电压220 V、效率0.75、极数为4、槽数为12、气隙厚度5 mm、极距39.27 mm。

图11 单边直线感应电机的实验模型Fig.11 Experimental model of SLIM

实验时，使电机工作在空载运行状态，并通过速度传感器测量其空载平移速度。取达到稳态后300 ms内的速度测量值，并与前文的解析法、有限元法进行比较，可以得出图12。

从图12可以看出:有限元法和实验实测得到的空载平移速度均超过了由电机本身机械尺寸所得的机械同步速度，却没有超过由解析法得到的同步速度。这就验证了:对初级铁心开断的单边直线感应电机，空载平移速度只是超过所谓的机械同步速度，并未超过本文提出的通过等效电磁极距计算得到的同步速度。

图122 p=4，δ=5 mm时不同方法得到的稳态速度对比Fig.12 Comparison of speed in steady state by different method

相对于实验法，有限元仿真是在较为理想的条件下进行的，忽略了机械磨损、风阻等因素的影响，所以有限元法得出的速度值超过机械同步速度更多，而实验测得的速度值超过很少。

5 结论

本文通过利用麦克斯韦方程组对单边直线感应电动机空载气隙磁通密度的解析计算和有限元仿真验证得出如下结论:

1)提出一个新的物理量“等效电磁极距”

基于电磁场分析，对于铁心开断的直线弧形电机或初级有限长的直线感应电机在两个端部的散漏磁通，本文提出了考虑纵向端部效应影响的“等效电磁极距”的概念。

2)空载速度并未超过同步速度

对于铁心开断的直线弧形电机或初级有限长的直线感应电机，通常所谓的同步运行速度是指由电机本身机械尺寸上的极距而计算得到的(VS=2fτ)，基于电磁场分析本文提出了考虑纵向端部效应影响的“等效电磁极距”的概念和计算同步运行速度的新的方法(VS=2fτE)。即:本文开头所述电机的空载运行速度只是超过了由机械极距而得的同步速度，并没有超过由等效电磁极距计算而得的同步速度。

3)同步速度与气隙厚度的关系

随着气隙厚度的增加，定、转子(初、次级)间的磁场耦合程度下降，气隙磁通密度的幅值减小，但在有限长初级端部的散漏磁通的数量增加，端部磁通密度呈现增大的趋势，这在一定程度上会导致电机的同步速度(等效电磁极距)增加。

4)给出不同极数下对机械极距的修正系数

为得出相对精确的同步运行速度，在保证其他条件不变的情况下，本文得出了电机在不同极数下对机械极距的修正系数。并绘制出修正系数以极数为变量的变化曲线。可以看到随着极数的增加，纵向端部效应对同步运行速度的影响逐渐减小，并趋近于机械同步速度。通常当极数大于6时，可以忽略端部效应对同步运行速度的影响。

［1］NASAR S A，BOLDEA I.Linear motion electric machines［M］.Sciense Press，1982:57－76.

［2］YAMAMURA S.Theory of linear induction motors［M］.University of Tokyo Press，1978:78－83.

［3］HAMZEHBAHMANI Hamed.Modeling and simulating of single side short stator linear induction motor with the end effect［J］.Journal of Electrical Engineering，2011，62(5):302－308.

［4］LIU Junyong，MA Weiming，LI Langru.Research on longitudinal end effect of high speed long primary double-sided linear induction motor［J］.Proceedings of the CSEE，2008，28(30):73－78.

［5］ZAREBAZGHALEH A，NAGHASHAN M R，MAHMOUDIMANESH H，MESHKATODDINI M R.Effective designparameters on the end effect in single-sided linear induction motors［J］.World Academy of Science，Engineering and Technology，2010，40(6):95－100.

［6］龙遐令.直线感应电动机的理论和电磁设计算方法［M］.北京:科学出版社，2006:62－67.

［7］SELCUK A H，HASAN Kürüm.Investigation of end effects in linear induction motors by using the finite-element method［J］.IEEE Transactions on Magnetics，2008，44(7):1791－1795.

［8］张宏.直线感应电动机端部效应研究［J］.榆林学院学报，2008，18(4):45－47.

ZHANG Hong.Research on end-effect of linear induction motor［J］.Journal of Yulin Institute，2008，18(4):45－47.

［9］上官璇峰，汪旭东，袁世鹰.直线电机纵向边端效应分析［J］.焦作工学院学报，1997，16(6):42－45.

SHANGGUAN Xuanfeng，WANG Xudong，YUAN Shiying.Analysis of longitudinal end-effect in linear induction motor［J］.Journal of Jiaozuo Mining Institute，1997，16(6):42－45.

［10］陈世坤.钢次级平面型直线异步电动机的一些设计计算问题［J］.中小型电机技术情报，1976，6(6):8－12.

CHEN Shikun.Design and calculation of linear induction motor with steel-secondary［J］.Medium or Small Electric Machine Technical Information，1976，6(6):8－12.

［11］高月春，熊光煜.直线异步电机空载气隙磁场的计算分析［J］.太原理工大学学报，1999，14(3):246－249.

GAO Yuechun，XIONG Guangyu.Analysis and calculation of airgap magnetic field in linear induction motor［J］.Journal of Taiyuan University of Technology，1999，14(3):246－249.

［12］陈红艳.直线感应电机电磁特性数值计算与仿真设计［D］.成都:西南交通大学电气工程学院，2008，6:11－21.

［13］GIERAS J F，DAWSON G E，EASTHAM A R.A new longitudinal end effect factor for linear induction motors［J］.IEEE Trans-actions on Energy Conversion，1987.3，EC－2:152－159.

［14］RENATO Crivellari Creppe，JOS＇E Alfredo Covolan Ulson，JOS＇E Francisco Rodrigues.Influence of design parameters on linear induction motor end effect［J］.IEEE Transactions on Energy Conversion，2008，23(2):358－362.

［15］焦留成，朱建铭，袁世鹰.直线感应电动机结构参数对功率因数及效率的影响研究［J］.焦作矿业学院学报，1995，14(6):71－77.

JIAO Liucheng，ZHU Jianming，YUAN Shiying.Research about effect on power factor and efficient of structure parameter in linear induction motor［J］.Journal of Jiaozuo Mining Institute，1995，14(6):71－77.

［16］黄波.直线感应电机的电磁力研究［D］.成都:西南交通大学电气工程学院，2007，4:7－24.