无线传感器网络中基于有效三角形判定的改进APIT定位方法*
2014-09-20汤大权史宗麟
谭 真, 汤大权, 史宗麟
(国防科技大学 信息系统工程重点实验室,湖南 长沙 410073)
0 引 言
无线传感器网络(wireless sensor networks,WSNs)是由大量具有独立数据采集功能传感器节点组成的、基于任务的信息采集平台。由于部署方便、快捷,其应用范围十分广泛,如环境检测、灾害防护、交通检测、目标跟踪等[1,2]。在无线传感器网络中,传感器节点自身位置的确定,即节点自定位是网络的基本功能,它在无线传感器网络应用领域中具有重要意义。它不仅可以确定发生感知数据的具体地理位置或者相对某一个参照系的位置,为进一步跟踪目标奠定基础;而且可以通过自定位信息选择最短的路径传输信息,使得在提高路由效率的同时减少通信开销。
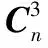
现阶段,很多人针对如何降低传感器能耗问题进行研究。Jung Deokwoo提出了一种交叉使用高能耗和低能耗的传感器来降低传感器的能耗,这种利用增加硬件来降低能耗的方法增加了使用成本[3];Coleri S和 Ergen M提出了一种混合数据模型的传感器生命周期分析方法[4],但其算法不满足节点随机分布的特性;Wu Lidong提出了一种用最少传感器覆盖所有探测区域的方法[5],该方法有效提高传感器的使用率,但无法进行节点自定位。
针对APIT定位算法存在的算法复杂度高、定位过程能耗较大的问题,本文提出了一种利用分离定理和面积法排除无效三角形的方法,该方法可以有效地减小定位方法的计算量,降低通信能耗,以此延长无线传感器网络的寿命。
1 APIT方法及其缺陷
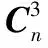
APIT定位算法的理论基础是三角形内点测试(perfect point-in-triangulation text,PIT)法。PIT的基本原理如图1所示,假设存在一个方向,节点M沿着这个方向移动会同时远离或接近顶点O,P,Q,那么节点位于△OPQ外;否则,M位于△OPQ内。在传感器网络中节点通常是静止的,文献[2]为了在静态的环境中实现三角形内点测试,提出了APIT法:假如在节点M的所有邻居节点中,相对于节点M没有同时远离或靠近3个信标节点O,P,Q,那么节点M位于△OPQ内;否则,节点M位于△OPQ外。
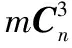
2 改进APIT方法
针对上述APIT算法的不足,研究人员提出了很多的改进方法,周四清提出了一种IAPIT方法,该方法提高了算法定位的精度,但大幅度地增加了硬件成本和能量消耗[6],本文提出了一种只针对有效三角形进行APIT的方法,即在进行APIT前判断该三角形是否为有效三角形,若为无效三角形,则不需要进行APIT算法。这样大大减少了APIT的次数,因此,减少了自定位过程中的通信量,降低了节点能耗,增加了网络寿命。
首先说明2个定理:
定理1 分离定理[7]:平面上2个三角形不相交,当且仅当在这2个三角形的所有边中至少存在一条边,这2个三角形位于这条边所在直线的异侧。
定理2 面积法[7]:如果△PBC,△PAB和△PAC的面积之和与△ABC的面积相等,即可判定点P在△ABC内(包括在三条边上)。
2.1 算法描述
本文提出的APIT改进方法使用了上述2个定理。其定位步骤如下:
1)初始化构造三角形:假设在目标定位区域存在一个三角形将所有的传感器节点包括在内。所谓构造三角形就是人为构造一个将未知节点包括在其内部的三角形。
2)遍历三角形:用面积法和分离定理判断所遍历的三角形是否是无效三角形,若为无效三角形,则排除;若为有效三角形,则进行APIT算法,然后判断有效三角形的面积是否小于构造三角形,若小于,则将当前的有效三角形视为构造三角形。所谓有效三角形就是与构造三角形相交或内含与构造三角形的三角形;反之,即为无效三角形。
3)求质心:对包含未知节点的所有三角形求交集,即为未知节点所在区域,求其质心,得到未知节点的位置。
2.2 算法举例
2.2.1 初始化三角形
如图1所示在目标定位区域设计一个大的△OPQ,记为最初的构造三角形,记录其所有边的函数,计算三角形的面积,将节点所感知区域内的所有的传感器节点都包括在内。
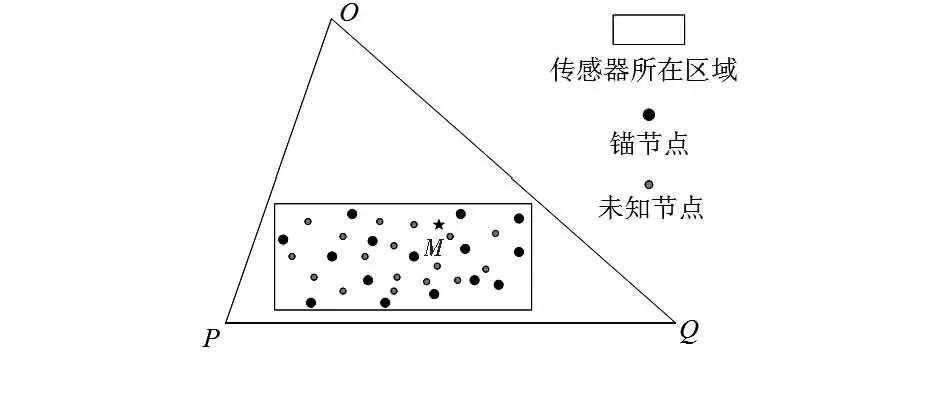
图1 初始化三角形
2.2.2 遍历三角形
1)对于任意一个所遍历的△ABC,利用面积法判断其是否包含传感器所在的△OPQ,若包含如图2(a),则△ABC内部的所有栅格加1,然后遍历下一个三角形(break)。
2)利用分离定理判断所遍历的△ABC是否与当前的△OPQ相交,若不相交,如图2(b),则△ABC内部的所有栅格减1,然后遍历下一个三角形(break)。
3)使用APIT算法,判断传感器节点是否在所遍历三角形内部:
a.若在传感器节点在所遍历△ABC内部,则将△ABC内部的所有栅格加1,然后比较△ABC同△OPQ的面积;若当前S△ABC
b.若在传感器节点在所遍历△ABC外部,如图2(d)所示,则△ABC内部的所有栅格减1,然后进行下一次遍历(break)。
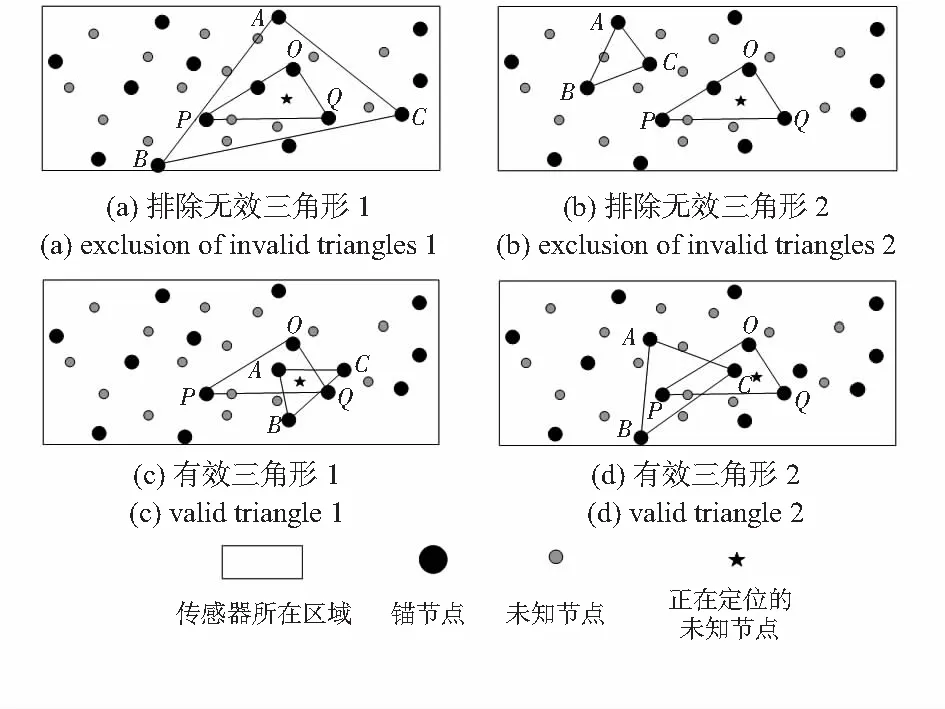
图2 遍历三角形
2.2.3 栅格法求质心
最终将栅格内的最大数所在区域记为传感器所在区域,所在区域栅格的个数记为Count,求出所在区域的质心(X,Y)即视为传感器的坐标所在地,如图3所示,质心公式如下
其中,Xi,Yj为每个栅格的中心点坐标。
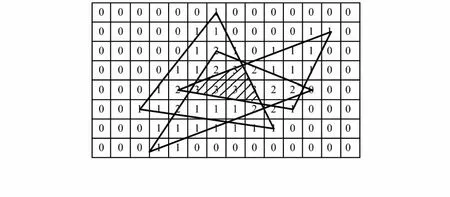
图3 利用栅格法求质心
2.3 算法设计
假设未知节点M周围有N个邻居信标节点,则每次APIT的算法复杂度为O(N),而利用分离定理和面积法判断三角形是否是无效三角形的算法复杂度为O(1),所以,排除无效三角形法可以有效降低算法复杂度。APIT改进算法如下:
square_random(1000,300,0.2);%布置节点 GPS误差为0
model=‘Regular Model’;%选择通信模型
Init Triangle();%初始化三角形
fori=unknown_node_index %遍历所有节点
fora=1:neighboring_anchor_n-2%遍历所有三角形
forb=a+1:neighboring_anchor_n-1
forc=b+1:neighboring_anchor_n
if(squaremethod( Triangle[a,b,c])>0)
%面积法排除无效三角形
break;
elseif(separate theorem(Triangle[a,b,c])>
0)
%分离定理排除无效三角形
break;
else
APIT(grid_length);%使APIT定位
end
end
end
end
gird(Triangle[a,b,c]) ;%栅格法求质心
end
3 仿真实验
在基于APIT的自定位算法过程中,影响定位精度与能耗的条件有很多:1)信标节点在节点中所占的比例:所占比例越大,定位的精度越高,但定位的复杂度就越高,能耗就越大。2)节点的分布状况:信标节点的分布对定位的精度有很大的影响,当未知节点不再任何一个信标节点构成的三角形内部时,就无法达到定位的效果。3)栅格的大小:栅格越小,定位的精度越高,但是太小的栅格就使传感器的能耗大大增加,进而导致传感器的使用寿命降低。
本文就APIT与其改进算法分别做仿真,以此比较两者的优劣。
3.1 仿真实验参数
本文采用Matlab进行仿真,仿真参数如表1所示。在仿真实验的过程中,着重考虑算法的精度和复杂度,并针对算法的复杂度进行分析,并以信标节点个数的变化作为条件统计APIT使用次数,以此项指标判断算法的有效性。
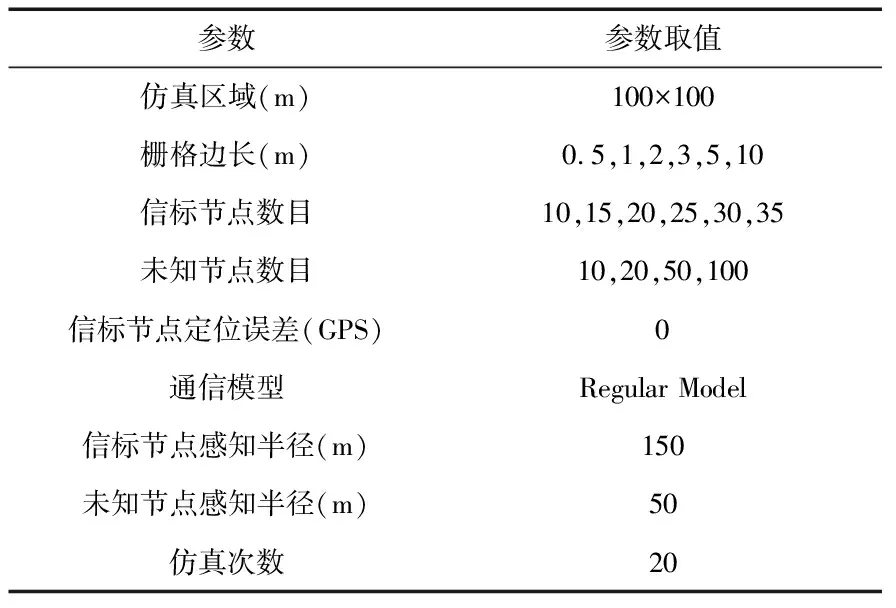
表1 仿真实验参数设置
3.2 实验结果比较
3.2.1 APIT次数统计比较
由文献[2]可知,每次进行APIT时,自定位节点都需要和周围的信标节点进行至少一次通信,而通信的过程即是消耗能量的过程,所以,在实验中可以通过统计每次定位过程中所需要的APIT次数来近似测算节点所消耗的能量。实验中假设在长、宽各为100 m的区域中部署了100个未知节点,信标节点的个数从10个一直增加到35个,图4展示了在信标节点个数不同的情况下APIT的次数。改进算法在APIT次数明显低于原算法,尤其在信标节点个数为30时改进算法的APIT次数较原算法降低了53 %。由此可见改进后的算法将大大降低计算量,以此为节点节省大量能量。
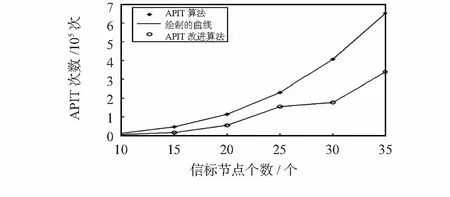
图4 APIT的次数
3.2.2 能耗比较
通常1 bit的信息传输100 m距离所需要的能量大约相当于执行3 000条计算指令所消耗的能量[8]。通过这一换算关系对算法的能耗进行仿真计算,结果如图5所示。相比较于APIT算法,改进后的算法在能耗方面有了很大的降低,当信标节点为20时降低大约42 %。这是由于改进算法在计算的过程中大大减少了未知节点与周围节点的通信。从而使能耗的大大降低,传感器的使用寿命延长。
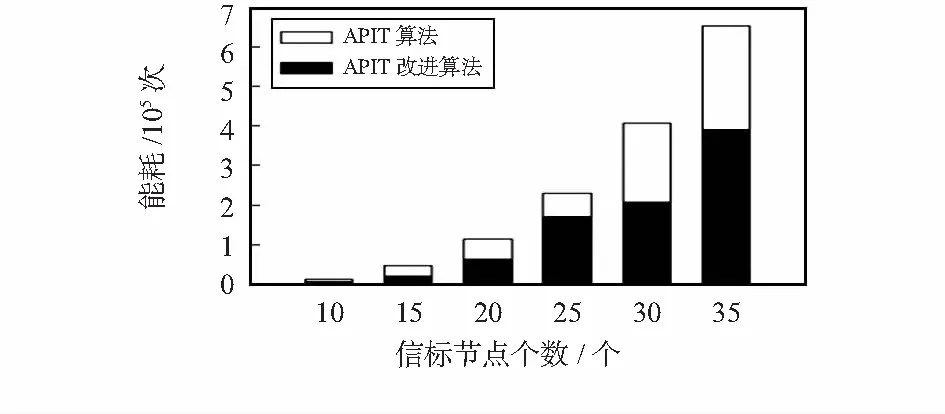
图5 能耗比较
3.3 定位误差比较
所谓定位误差,就是未知节点实际未知与估计未知之间的距离与通信半径之间的比值。
1)栅格大小对定位误差的影响
本文通过改变栅格大小仿真栅格边长对定位精度的影响。在仿真过程中,未知节点的通信半径为50 m,得到结果如图6。通过观察发现,当栅格边长较小时,改进的APIT算法定位误差略高于APIT算法的定位误差,当栅格的大小增加到通信半径的1/10时,改进后APIT算法的定位误差将高于原APIT算法的误差,这时不宜采用改进的APIT 算法。
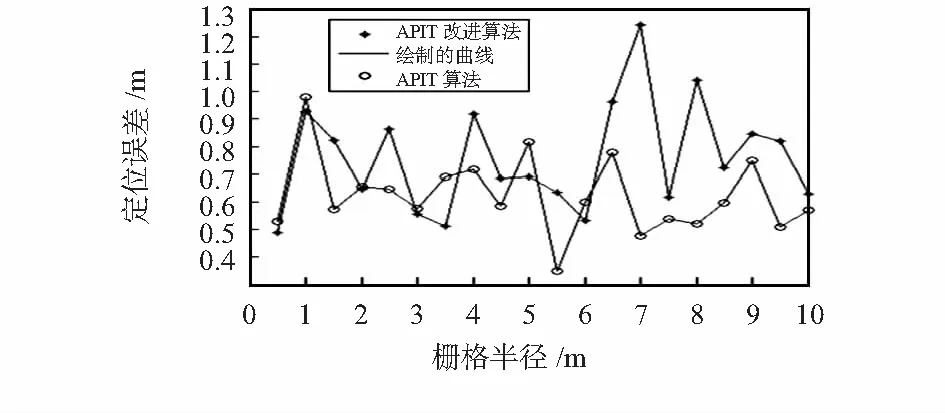
图6 栅格大小对定位误差的影响
2)信标节点个数对定位误差的影响
为了进一步研究信标节点个数对定位误差的影响,设置栅格边长为2 m,分别对信标节点个数为10,15,20,25的情况进行仿真实验,定位误差结果如图7所示。从结果来看,改进后算法的定位误差有所增大,但与原算法十分接近,因此,改进后算法的定位结果准确、可靠。
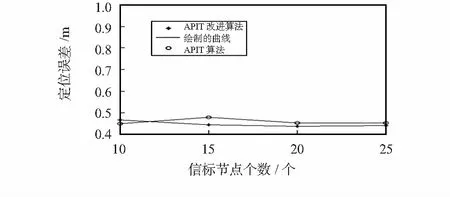
图7 信标节点个数对定位误差的影响
4 结束语
本文利用面积法和分离定理提出了一种排除无效三角形的方法来改进APIT算法,降低算法的复杂度,以此降低能耗,增加网络寿命。仿真实验结果表明:该方法可以在不失定位精度的同时大量减少APIT的次数、降低能耗、增加传感器网络的使用寿命,有效解决了原APIT能耗问题,满足了用户对增加网络寿命的需求。
参考文献:
[1] 孙利民.无线传感器网络[M].北京:清华大学出版社,2005.
[2] He T,Huang C,Blum B M,et al.Range-free localization schemes for large scale sensor networks[C]∥Proc 9th Annual Int’l Conf on Mobile Computing and Networking (MobiCom),San Diego,CA,2003:81-95.
[3] Jung Deokwoo ,Savvides Andreas .An energy efficiency evaluation for sensor nodes with multiple processors,radios and sensor-s[C]∥Proceedings of IEEE INFOCOM 2008 ,Palma De Mallorca,Spain,2008:1112-1120.
[4] Coleri S,Ergen M.Lifetime analysis of a sensor networkwith hybrid automata modeling[C]∥1st ACM International Workshop on Wireless Sensor Networks and Applications(WSNA),Turin,2002.
[5] Wu Lidong ,Du Hongwei,Wu Weili.Approximationsfor minimum connected sensor cover[C]∥Proceedings of IEEE INFOCOM 2013,Italy,2013:1188-1194.
[6] 周四清,陈锐标.无线传感器网络APIT定位算法及其改进[J].计算机工程,2009,35(7):87-89.
[7] 何大华,陈传波.两个三角形不相交的充要条件[J].应用数学, 2002 (1):37-41.
[8] 赵 静,潘 斌,王 进,等.无线传感器网络能耗分析与策略研究[J].通信技术,2010,10(43):85-89.
[9] Jung D,Teixeira T,Barton-Sweeney A.Model-based design exploration of wireless sensor node lifetimes[C]∥European Confe-rence on Wireless Sensor Networks,EWSN’07,Chicago,2007:277-292.
[10] Li Xinrong.Collaborative localization with received-signal strength in wireless sensor networks[J].IEEE Transactions on Vehicular Technology,2007,56(6):3807-3817.
[11] Wang C,Wang G.Reconciling privacypreservation and intrusion detection in sensory data aggregation[C]∥Proceedings of 31th IEEE International Conference on Computer Communications,Seoul,Korea,2011:336-340.
