液压衬套集总参数模型动态特性液－固耦合有限元分析

李 林，曾祥坤

（1．广东轻工职业技术学院 汽车系，广州 510300；2．华南理工大学 机械与汽车工程学院，广州 510641；3．广东技术师范学院 机电学院，广州 510665）

径向型液压衬套是汽车底盘隔振系统中广泛应用的新型隔振器，极大程度地改善了车辆操纵稳定性和平顺性［1－2］。液压衬套非线性动态性能的研究以集总参数模型分析为主，但动特性的计算结果是否与实验结果吻合，很大程度上取决于模型中物理参数的准确性［3］。目前，这些物理参数的获得大多依赖于实验测试或近似解析公式，这在识别精度及预测成本等方面有较大的局限性［4－5］。因此，提出一种不依赖实验样件制作的液压衬套集总参数及动特性的高效辨识预测方法尤为重要。

随着计算机及有限元技术的发展，液－固耦合有限元非线性分析方法采用 ALE（Arbitrary Lagrangian Eulerian）描述来处理液体－固体耦合边界的大位移运动，使直接预测计算液压衬套非线性动力学特性成为可能［6－11］。近年来，国内外一些学者采用非线性有限元技术主要对动力总成液阻悬置的液压阻尼特征进行了相关研究。Foumai等［6］采用有限元分析方法得到惯性通道式液阻悬置橡胶主簧的刚度、体积柔度和等效活塞面积，但文中仅给出了橡胶主簧轴对称结构的有限元模型、橡胶材料的超弹性本构模型和计算得到的橡胶主簧的力－变形曲线。Muller等［7］利用ANSYS和FLUENT有限元商业软件配合，计算一液压悬置轴对称橡胶主簧的体积柔度的方法，但该方法只能进行单向液－固耦合有限元分析，且文中未提及其他参数的识别方法。上官文斌等［12－14］在实验测试的基础上，研究了惯性通道－活动解耦盘式液阻悬置及其橡胶主簧静、动态特性的有限元分析方法，对液－固耦合有限元分析中有关的一系列计算和建模方法进行讨论，探讨了利用有限元仿真技术辨识集总参数的可行性。目前发表的文献，还未应用非线性有限元分析技术对液压衬套集总参数识别及动力学特性预测展开全面研究。

文中以径向型液压衬套为研究对象，建立其动力学特性分析的集总参数模型，基于ADINA有限元软件平台，采用双向耦合的液－固耦合有限元分析方法辨识模型中的主要物理参数，并对其动态特性进行计算分析。探讨了低成本前提下精确预测液压衬套集总参数模型的参数及动态特性的可行性。

1 双向液－固耦合的有限元分析理论

液 －固耦合（Fluid-Structure Interaction，FSI）问题中，液体的作用力引起结构的变形，同时结构的大位移又影响流场的形态，这种类型叫做双向耦合的液－固耦合分析。双向耦合的液－固耦合方程是非线性方程，因此需要用迭代的方法得到某一时刻的解。也就是说，计算得到的是液－固耦合问题的迭代解X1、X2、…，根据应力、位移或者两者的结合来检查迭代的收敛性［15］。

应力的标准是

位移的标准是

式中和分别表示液体和结构的位移和分别为液体和结构的应力，下划线表示这些值只定义在液－固耦合界面上，n为耦合边界上的法线方向；ετ、εd分别是应力和位移收敛的容许误差，ε0是事先给定的常数（≡10－8）。

2 径向型液压衬套动特性分析的集总参数模型

径向型液压衬套液室及惯性通道的布置情况见图1（a）。根据径向型液压衬套的工作原理，建立其集总参数模型见图1（b）。模型中，Kr与 Br分别为橡胶主簧的刚度和阻尼系数；Ap为活塞的等效面积；Ii、Ri分别为惯性通道中液体的惯性系数和惯性通道对其中液体流动的流量阻尼系数。KV＝Kv1＋Kv2，BV＝Bv1＋Bv2，其中Kv1与Kv2（单位为N／m5）表示两液室的体积刚度，Bv1与Bv2（单位为N·s／m5）为两液室的体积膨胀阻尼。KVV和BVV分别为 KV和 BV的等效线刚度和等效黏性阻尼［1］。

根据液体的连续方程和动量方程以及激励与动反力的关系，得到液压衬套的复刚度为：

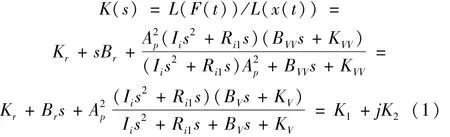
液压衬套动刚度，滞后角 φ＝arctg（K1／K2），阻尼系数 C＝Kdsin（h）／ω。

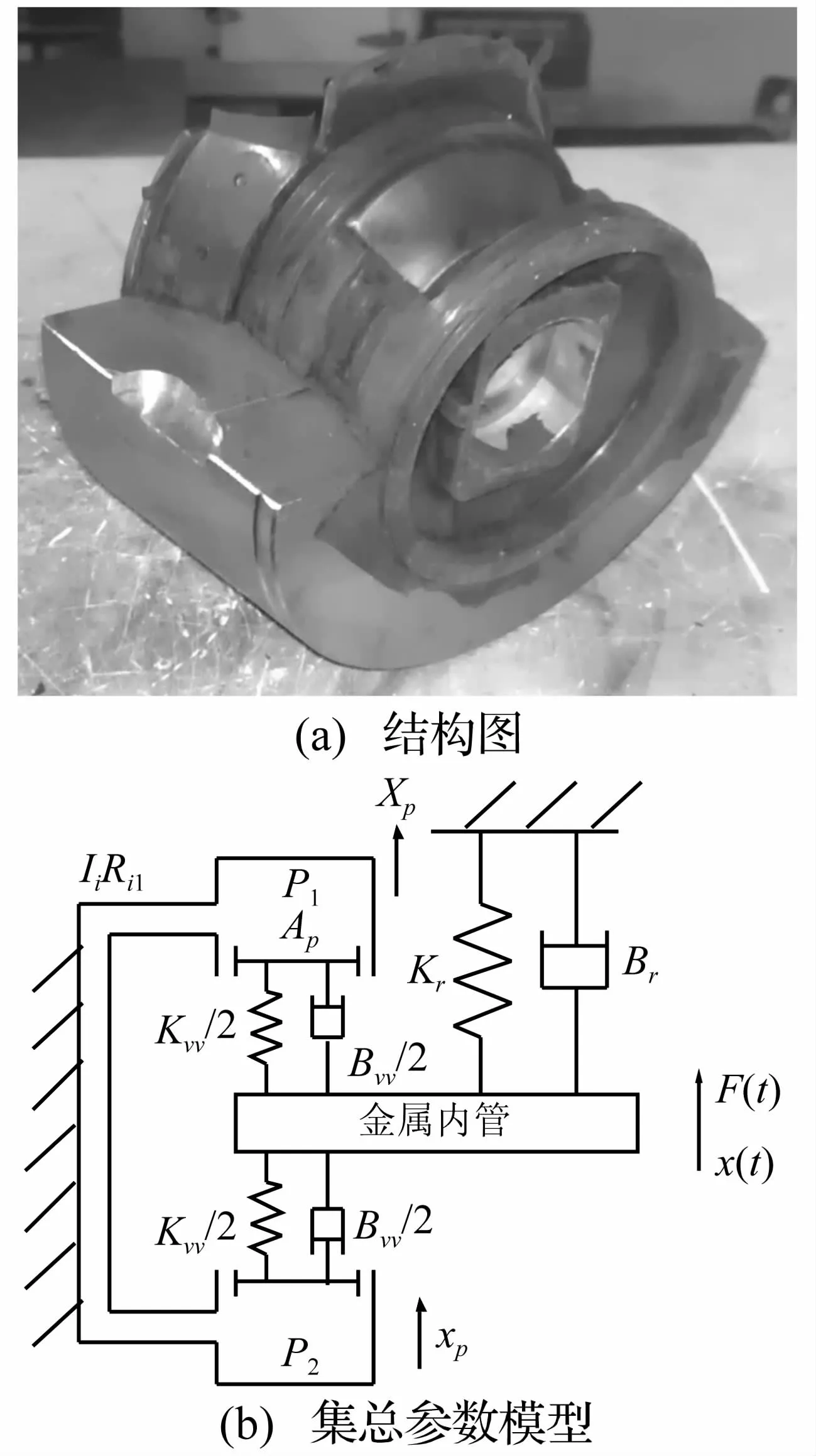
图1 径向型液压衬套Fig．1 The radial hydro-bushing

3 液压衬套集总参数模型有限元分析方法的参数识别

集总参数模型中的主要物理参数 Kr、Br、Kv1、Ap、Ii、Ri一般由实验方法或者由近似解析公式计算得到，但是通过这些方法获得的参数精度，与公式变化范围、实验条件和实验人员等因素有关，而且实验花费成本较高、周期较长，并且液压衬套内部流体的运动规律、压力分布等情况实验或解析公式是无法获取的。为了提高参数识别的精度，降低成本，文中采用非线性液－固耦合有限元分析方法辨识模型中的集总参数。

3．1 橡胶主簧的径向刚度Kr

橡胶主簧的动刚度可以由其静刚度Ks来表示：

式中：f为修正系数，取值范围为1．2～1．6之间。

图1（a）典型径向型液压衬套的结构图中，橡胶主簧的内外表面分别与金属内管、外管硫化在一起，起支撑和传力的作用。与橡胶的大变形相比，金属的变形可以忽略不计，不能影响主要流场的特性。按照有限元分析建模的简化原则，有限元模型中只考虑橡胶件对变形影响比较显著的特征，对变形影响较小的特征进行简化。金属外管固定安装在车架上，因此，在进行边界条件定义时，令该面上所有节点的位移为零。

图2为橡胶主簧的简化模型。橡胶材料选用超弹性本构关系中的Mooney－Rivlin模型，橡胶主簧内表面施加位移载荷。网格剖分采用Delaunay法，选用四面体的4／1单元，单元的最大尺寸为5 mm。橡胶主簧的有限元模型共有18 917个单元、4261个节点。

计算得到的橡胶主簧径向静刚度为320 N／mm，橡胶主簧在径向方向力－位移曲线的计算结果与前期研究实验结果的对比见图3。由图可见，随着位移的增加，橡胶主簧静刚度有所增大；计算值与实验值较吻合。取修正系数为f为1．6，计算得到橡胶主簧的动刚度为512 N／mm。

图2 橡胶主簧的简化模型Fig．2 The simplified model of rubber spring

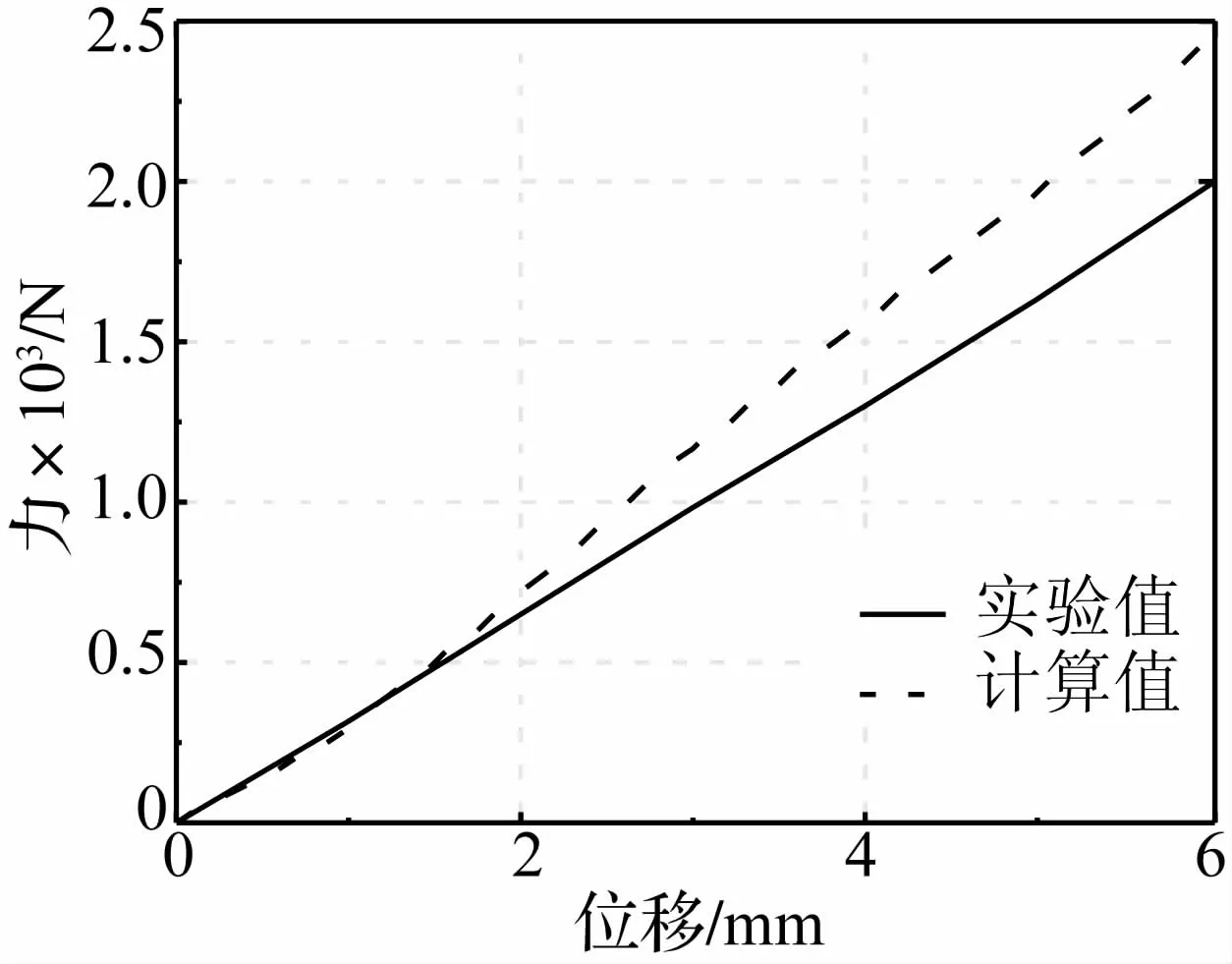
图3 橡胶主簧径向力－位移特性曲线Fig．3 Radial force-displacement curve of rubber spring

3．2 橡胶主簧的径向阻尼

橡胶主簧阻尼系数表达式：

其中：M为橡胶主簧的质量，ξr为橡胶材料的阻尼比，实验得到硬度为邵氏50度的天然橡胶的阻尼比为0．069，计算得到橡胶主簧的阻尼系数为138 N·s／m。

3．3 液室的体积刚度

在外部激励作用下，液压衬套金属内管相对金属外管发生位移，引起橡胶主簧膨胀变形时，液室内部压力变化与体积变化之比称为液室体积刚度。为计算体积刚度构建的固体模型如图4（a）所示。固体有限元模型中凹陷内腔表面为与液体相接触的面，定义为液－固耦合面，外管表面所有节点位移为零。

图4 计算液室体积刚度的有限元模型Fig．4 Calculated finite element model of chamber volume stiffness

图4 （b）为计算液室体积刚度所需的液体模型，液体的密度和黏度视为常数，定义为不可压缩流体。液体与橡胶衬套接触的内弧面定义为液－固耦合面；液体外表面与液压衬套外管接触，形成液室，定义为刚性不可滑移的壁面，同时在此面上加载速度载荷。

液体模型外表面施加均匀的速度载荷后，由于液体是不可压缩的，因此液室产生压力，使得橡胶衬套产生膨胀变形。通过液－固耦合有限元分析可以求出液室的均布压力；由加载速度、液体外表面的面积和加载时间可以求出流进液室的液体体积。对于不同加载速度，可以得到液室的压力与体积的关系，进而求出液室的体积刚度。计算得到液室的压力变化和体积变化之间的关系曲线见图5，液室的体积刚度计算值为57×108N／m5。

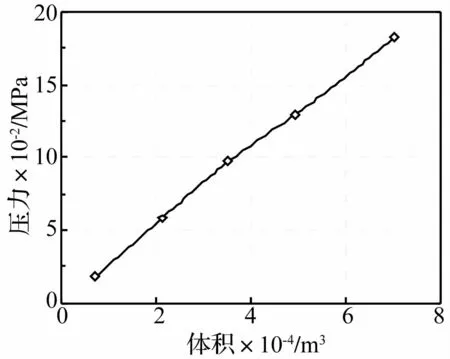
图5 液室的体积与压力的关系Fig．5 Volume-pressure of the chamber

3．4 橡胶等效活塞面积

外部激励作用下，橡胶主簧发生径向振动位移x时，液室内部液体体积的变化量等于等效活塞面积Ap所排出的体积。即：

计算橡胶等效活塞面积的几何模型与计算液室体积刚度的几何模型一致，有限元模型的定义也基本相同，只是载荷条件有所区别。固体有限元模型内管施加径向位移载荷x后，可以求出橡胶内腔的径向位移xp，由xp和液体外表面的面积即可求出液室体积的变化，即为所排出液体的体积。

记录不同径向位移载荷作用下xp的变化，计算得到的橡胶等效活塞面积和橡胶径向位移之间的关系见图6。由图可见，当橡胶的径向位移大于2 mm后，等效活塞面积基本保持不变，其大小与激励的振幅和频率无关。计算得到的等效活塞面积为4．13×10－2m2。

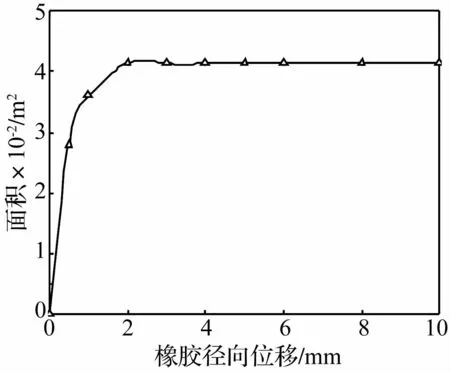
图6 橡胶等效活塞面积Fig．6 The equivalent rubber piston area

3．5 惯性通道中液体的惯性系数和流量阻尼系数

液体在惯性通道内的动量方程为：

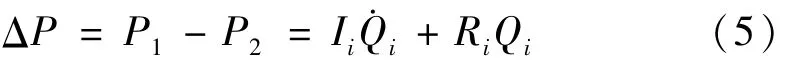
将式（5）进行拉氏变换，其频域表达式为：

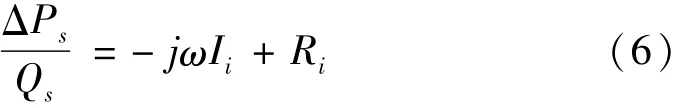
因而只要得到惯性通道两端压力差ΔP与流经惯性通道的液体流量之间的幅频特性，就可以识别出流体流经惯性通道时的惯性系数和流量阻尼系数。

计算所需的固体模型与图2所示的模型相同，液室内壁定义液－固耦合面。液体模型由两个液室和惯性通道内的液体组成，在一侧液室的外弧面上施加压力载荷；液室及惯性通道的外表面与外管接触，定义为刚性不可滑移的壁面；其他的面与橡胶接触，定义为液－固耦合面，如图7所示。

对图7所示的有限元模型进行液－固耦合分析时，液体模型所施加的压力载荷的大小与时间成正弦曲线变化关系，记录不同频率下惯性通道另一端流量的变化，根据式（6）计算可得液体流经惯性通道时的质量惯性系数Ii和流量阻尼系数Ri。

由图8可见，当惯性通道两端压力差的变化频率较低时，液体流经惯性通道时的惯性系数和流量阻尼系数基本变化不大，识别得到的参数 Ii＝1．56×104kg／m4，Ri＝2．5×106N·s／m5。

图9为激振频率40 Hz时惯性通道内液体流速的分布情况。随着频率的升高，惯性系数和流量阻尼系数都有增大的趋势，液体在惯性通道内的流动变得困难。这就导致液压衬套压力增加一侧的液室内部液体无法自由流向另一侧压力较低的液室，液压衬套传递的力相应增加，动刚度增大。

图7 液体有限元分析模型Fig．7 The finite element analysis model of the fluid

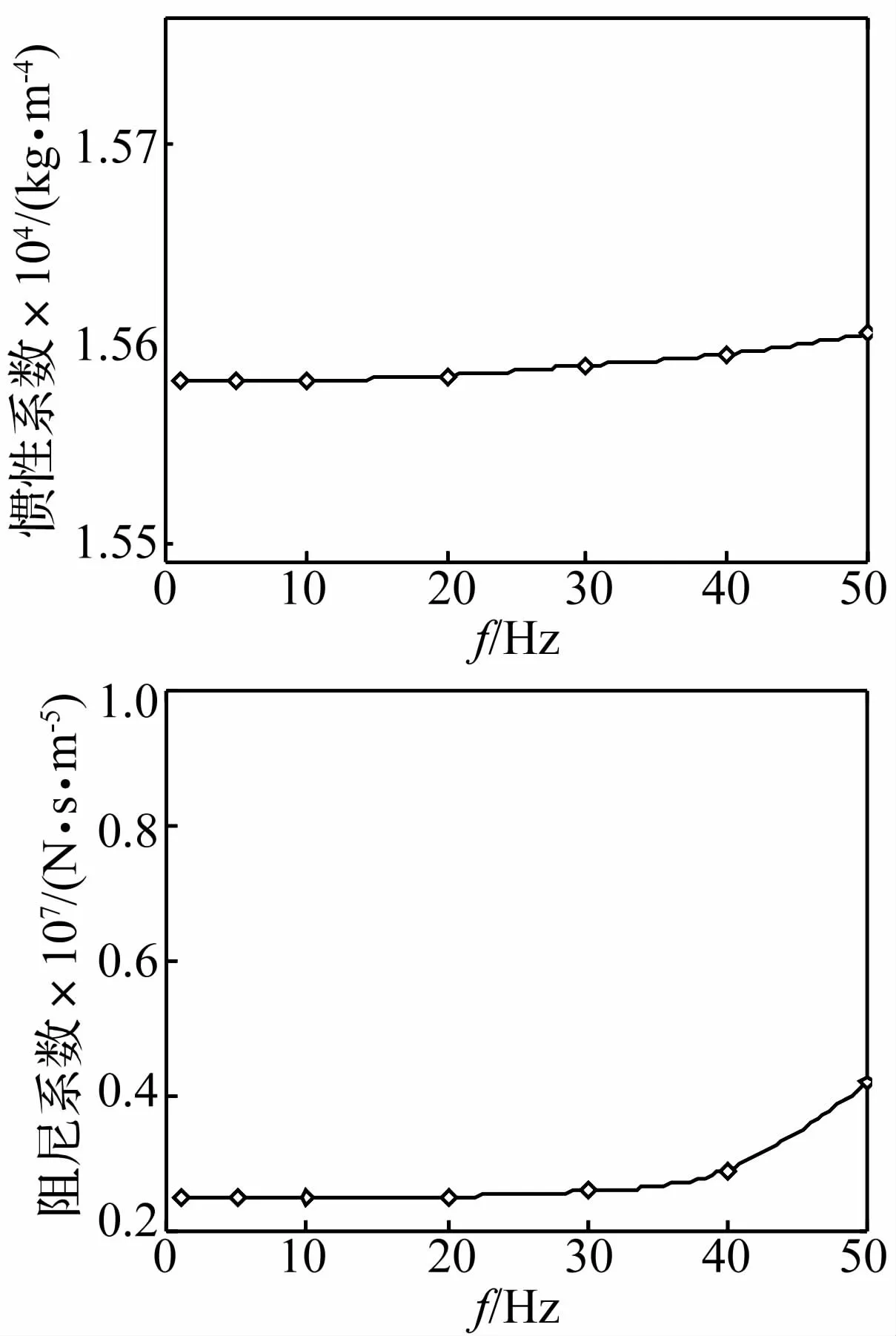
图8 不同频率下惯性通道惯性系数和阻尼系数Fig．8 Inertia and damping coefficients of inertia channel

图9 惯性通道中液体流速Fig．9 Fluid velocity in the inertia channel

3．6 集总参数识别结果分析

基于最小二乘参数估计的方法［16］和基于液－固耦合有限元集总参数识别的方法得到的结果以及两者之间的相对误差分析见表1。从表中可以看出，两种识别方法得到的大部分计算结果比较吻合，误差较小；只有橡胶主簧阻尼系数的识别误差相对较大，这主要是由于有限元计算过程中模型简化造成的。

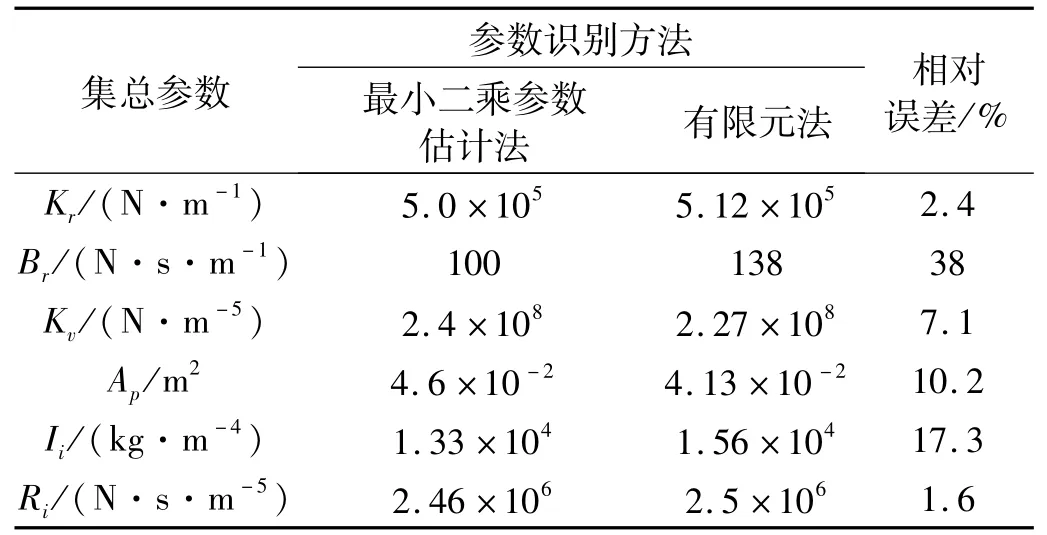
表1 两种参数识别方法结果及误差分析Tab．1 The results and error analysis of two parameter identification methods

4 径向型液压衬套动态特性的有限元计算分析

液压衬套动态特性的振幅相关性和频率相关性具有较强的耦合特征。采用图2所建立的固体黏弹性模型和图7液体模型对其动特性进行有限元分析，固体模型的分析类型选择动态显式算法，液体模型设置为瞬态分析模式。在进行动态特性计算时，不考虑温度及其对液体黏度、密度的影响，在橡胶衬套内管表面上施加径向谐波位移激励，其表达式为：

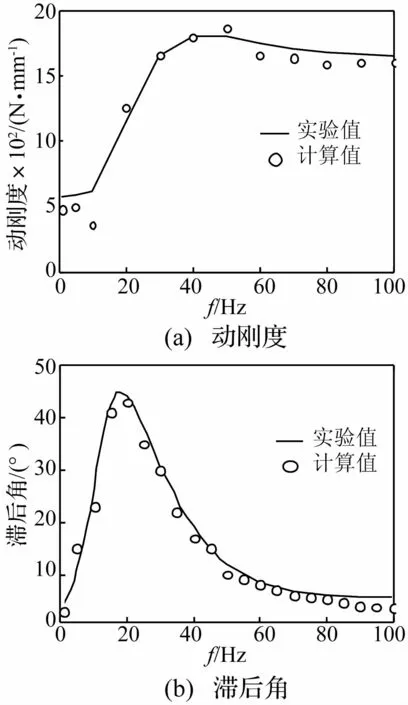
图10 径向型液压衬套动特性计算结果（振幅0．1 mm）Fig．10 Calculated dynamic characteristics of the radial hydro-bushing

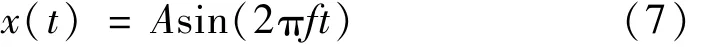
式中：A、f分别为动态位移激励的振幅和频率。

采用液－固耦合有限元方法计算得到的径向型单惯性通道式液压衬套的动刚度和滞后角见图10。通过与实验曲线的对比分析，其计算误差较小，而且较准确的预测了滞后角峰值出现的频率。与最小二乘参数估计得到的液压衬套的动态特性曲线相比较［16］，有限元法的计算结果与实验结果更加接近，因而可以认为利用有限元方法识别得到的液压衬套动态特性集总参数具有更高的精度。

5 结 论

（1）介绍了径向型液压衬套动特性分析的集总参数模型，建立了相应集总参数辨识的有限元模型，探讨了运用双向耦合的液－固耦合有限元分析方法识别集总参数模型中主要物理参数的计算方法和过程，对比分析了计算值与部分实验结果及最小二乘参数估计的结果，计算结果误差较小；

（2） 联合集总参数模型及液－固耦合有限元分析技术，对液压衬套动态特性进行仿真计算，通过与实验值及最小二乘拟合结果的对比，结果表明有限元法能准确的预测液压衬套的动力学性能，且其计算结果较最小二乘拟合结果具有更高的精度。

文中提出的研究方法在液压衬套产品开发设计阶段具有较高的工程应用价值，同样也适用于其他类型具有液压阻尼特征元件的设计优化。

［1］上官文斌，徐驰．汽车悬架控制臂液压衬套动态特性实测与计算分析［J］．振动与冲击，2007，26（9）：7－10．SHANGGUAN Wen-bin， XU Chi． Measurement and calculation analysis of dynamic characteristics for hydraulic bushing in controlling arm of vehicle suspension［J］．Journal of Vibration and Shock，2007，26（9）：7－10．

［2］Arzanpour S，Golnaraghi M F．Development of an active compliance chamber to enhance the performance of hydraulic bushings［J］．Journal of Vibration and Acoustics，2010，132：1－7．

［3］Gil-Negrete N．Predicting the dynamic behaviour of hydro-bushings［J］．Shock and Vibration，2002，12：91－107．

［4］Sauer W，Guy Y．Hydro bushings innovative NVH solutions in chassis technology［R］．SAE 2003－01－1475，2003．

［5］Arzanpour S．Active and semi-active bushing design for variable displacement engine［D］．Canada：University of Waterloo，2006．

［6］Foumani M S，Khajepour A，Durali M．Application of shape memory alloys to a new adaptive hydraulic mount［R］．SAE 2002－01－2163，2002．

［7］Muller M，Eckel H G．Reduction of noise and vibration in vehicle by an appropriate engine mount system and active absorbers［R］．SAE 960185．

［8］Christopherson J，Jazar G N．Dynamic behavior comparison of passive hydraulic engine mounts．Part 2：Finite element analysis［J］．Journal of Sound and Vibration，2006，290：1071－1090．

［9］Foumani M S，Khajepour A，Durali M．Application of shape memory alloys to a new adaptive hydraulic mount［R］．SAE 2002－01－2163，2002．

［10］Yoon J Y，Singh R．Indirect measurement of dynamic force transmitted by a nonlinear hydraulic mount under sinusoidal excitation with focus on super－harmonics［J］．Journal of Sound and Vibration，2010，329：5249－5272．

［11］ Garcia M J，Kari T L，Vinolas J，et al．Frequency and amplitude dependence of the axial and radial stiffness of carbon－black filled rubber bushings［J］．Polymer Testing，2007，26：629－638．

［12］Wang L R，Lu Z H，Hagiwara I．Integration of experiment and hydrostatic fluid－structure finite element ananlysis into dynamic characteristic prediction of a hydraulically damped rubber mount［J］．International Journal of Automotive Technology，2010，11（2）：245－255．

［13］Shangguan Wen-bin，Lu Zhen-hua．Experimental study and simulation of a hydraulic engine mount with fully coupled fluid-structure interaction finite element analysis model［J］．Computers and Structures，2004，82：1751－1771．

［14］Zhang Yun-qing，Shangguan Wen-bin．A novel approach for lower frequency performance design of hydraulic engine mounts［J］．Computers and Structures，2006，84：572－584．

［15］ Adina R，Adina D．Theory and Modeling Guide-ADINA-A and-F［M］．2010．

［16］李林．液压衬套动态特性实测分析及其集总参数模型建模研究［J］．振动与冲击，2013，32（22）：183－188．LI Lin．Experimental study and lumped parameter modeling analysis of dynamic characteristics for hydraulic bushing［J］．Journal of Vibration and Shock，2013，32（22）：183－188．