基于克隆选择和粒子群混合算法的导墙结构损伤识别

欧阳秋平，何龙军，2，练继建，陈媛媛，马 斌

（1．天津大学 水利工程仿真与安全国家重点实验室，天津 300072；2．交通运输部水运科学研究院，北京 100088；3．中水北方勘测设计研究有限责任公司，天津 300222）

结构损伤诊断可分为确定损伤是否存在、确定损伤位置、评估损伤程度以及预测结构剩余寿命4个层次［1］。近年来，利用模态信息的改变来检测结构损伤的方法已引起土木、机械和航空等工程界的广泛关注［2－5］。然而对于许多大型工程结构而言，人工激振是非常困难甚至是不可能进行的，所以，利用环境激励下的模态数据来识别结构损伤的方法已越来越引起人们的重视［6－7］。

导墙结构由于长期承受着高速水流和风等多种环境荷载的作用，在疲劳和腐蚀影响下容易发生开裂损伤，而若结构损伤发生在水下部分，则不易直接被发现，而且一旦发生损伤，在高速水流的激振作用下，破坏范围会迅速扩展，可能导致整个结构的失效［8］，如美国的Texarkana大坝、Trinity大坝和Navajo大坝的消力池导墙，均由于高速水流诱发了强烈振动而破坏［9］；我国的万安水利枢纽溢洪道导墙在运行中倒塌，乌江渡水电站左岸滑雪道右导墙出现强烈的流激振动现象等［10］。因此，为了保证水工结构的运行安全，就应对导墙结构进行定期的损伤检测，及早发现损伤并采取适当措施，避免造成人员伤亡事故和重大经济损失。由于大型水工结构的模态振型在实测中较难精确获得，且很多部位往往处于水下，测点布置受到很大限制，因此基于模态振型及其衍生指标的损伤诊断方法不适用于大型水工结构。因结构的模态频率比较容易获得且能保证较高的实测精度，所以在实际工程中更具应用价值［11］。

由于体积庞大及环境激励输入的未知性和随机性等因素，使结构损伤诊断在大型水工结构中的应用面临很大挑战。人工神经网络［12］、支持向量机［13］等智能算法都已在智能损伤诊断研究中采用。但是，人工神经网络和支持向量机算法在寻优时必须首先进行预测模型的训练，这就需要海量准确的样本信息作支持，工作量巨大。

基于智能算法的模型修正方法是近期结构损伤识别领域的研究热点之一［1，14－15］。它主要是通过智能算法的寻优能力，匹配结构的实测指标和有限元模拟指标以寻求反映结构真实性态的有限元模型，进而达到准确识别结构损伤位置和程度的目的。遗传算法和粒子群算法作为全局寻优算法，都力图在自然特性的基础上模拟个体种群的适应性，采用一定的变换规则通过搜索空间求解，而不需要海量的模态信息和预测模型训练。虽然遗传算法为全局寻优提供了一个比较可靠的工具，但是其在寻优性能上仍然存在很大的发展空间。粒子群算法自1995年被Kennedy等［16］提出以来，以收敛速度快、参数设置少、程序实现简单和具有深刻的智能背景等特点，在求解非线性不可微和多峰值的优化问题中表现出了较强的生命力。

因此，本文基于实数编码克隆选择和粒子群混合算法（A real encoding hybrid algorithm of clonal selection and particle swarm optimization，RCSA－PSO）优化模态频率指标，提出一种适合于环境激励下大型水工结构的智能损伤诊断方法。首先，提出了一种全局寻优能力更强的新型粒子群算法，通过不断更新有限元模型参数，可高效可靠地搜索到与实测信息匹配的结构损伤状态；其次，提出了基于低阶模态频率的损伤指标，并加入了损伤惩罚因子，以指导有限元模型与测试信息的匹配；第三，以某导墙的多工况损伤识别为例，研究了含噪声条件下该损伤诊断方法的识别效果，解决了导墙结构水下部分损伤检测难的问题，证明了该识别方法的适用性。

1 实数编码克隆选择和粒子群混合算法

1．1 实数编码粒子群算法

粒子群算法的基本思想是受他们早期对许多鸟类的群体行为进行建模与仿真研究结果的启发［17］。基本粒子群优化算法的思想可表述为：每个优化问题的潜在解都是搜索空间的粒子，所有的粒子都有一个被优化的函数决定的适应值，每个粒子还有一个速度向量决定他们飞行的方向和距离，然后粒子们就追随当前的最优粒子在解空间中的搜索。粒子群优化算法初始化为一群随机粒子，然后通过迭代找到最优解。在每一次迭代中，粒子通过跟踪两个极值来更新自己，第一个就是粒子本身到当前时刻为止找到的最好解，这个解称为个体最好值，另一个极值就是整个种群到当前时刻找到的最好解，这个值是全局最好值。在找到这两个极值后，粒子通过三方面来更新自己的速度和新的位置，包括粒子先前的速度，用来说明粒子目前的状态；个体的认知部分，使粒子有较强的全局搜索能力；以及社会共享信息，使粒子从其他优秀粒子中汲取经验，加强搜索能力［18］。于是微粒i在第d维子空间中的状态更新方程如下所示：

式中：上标k代表微粒i所在的步数，下标d代表微粒i的第d个维度，和分别为微粒i第d个维度在第k步和第k＋1步时的速度，和分别为微粒i的第d个维度在第k步时和第k＋1步时的位置，p为微粒i的历史最优位置，其与微粒i的当前位置之差的作用是指引该微粒向个体最优解靠拢；为微粒群的全局历史最优位置，其与微粒i当前位置之差的作用是确定当前微粒向全局最优值运动的分量；α为惯性权重；c1和c2为加速常数；r1和r2为（0，1）之间的两个相互独立的随机数；N为粒子群的规模；D为各粒子的维度。

为了同时对损伤位置和损伤程度寻优，本文采用实数编码形式来编写解变量。将可能产生损伤的位置和程度的数目作为粒子的维度，每一维度上的数值代表损伤发生的位置或程度，即按照［损伤位置1，损伤程度1，损伤位置2，损伤程度2，…损伤位置n，损伤程度n］进行编码。若对位置和程度进行归一化，则有xid∈［0，1］。例如，某结构共有3处可能存在的损伤，若算法寻找到的最优解为［0．2，0．5，0．5，0．3，0．7，0．4］T，则表明该结构的损伤位置发生在0．2、0．5和0．7位置处，相应的损伤程度为50%、30%和40%。可见，应用实数编码方式表示结构的损伤位置和损伤程度是十分方便和有效的。

1．2 实数编码克隆选择和粒子群混合算法

在粒子群优化算法的运行过程中，如果某粒子发现了一个当前最优位置，其他粒子将迅速向其靠拢，出现“聚集”现象，导致种群多样性的降低。如果当前所发现的最优位置是局部最优点，粒子群就有可能无法在解空间内重新搜索，算法陷入局部最优，出现早熟收敛现象。针对应用粒子群算法求解非线性优化问题过程中存在的早熟和收敛速度慢的问题，为提高粒子群算法的全局收敛性能，本文引入克隆选择算法［19－20］，提出了一种新型克隆选择和粒子群混合算法，并引入遗传算法中的变异操作作为克隆选择算法中的高频变异算子。

克隆选择算法是受到免疫系统启发而发展起来的仿生算法，是模拟自然界生物免疫系统的机理和功能而设计的算法，具有保持种群多样性的特点。本文在粒子群算法中融合免疫克隆选择算法的思想，首先根据粒子的亲和力对粒子执行按比例克隆复制，然后对克隆后的个体进行克隆高频变异，最后进行克隆选择，即从父代个体与子代个体中选择出最佳个体。成比例克隆复制可以使优良个体得到保护，加快算法收敛；高频变异为新粒子的产生提供了新的方法，维持种群多样性；克隆选择操作有效地避免了算法退化。因此，该混合算法可以增加种群的多样性，加快算法收敛速度，提高最优解的精度，具有更强的全局寻优能力。本文所提出的算法的实现思想如图1所示。

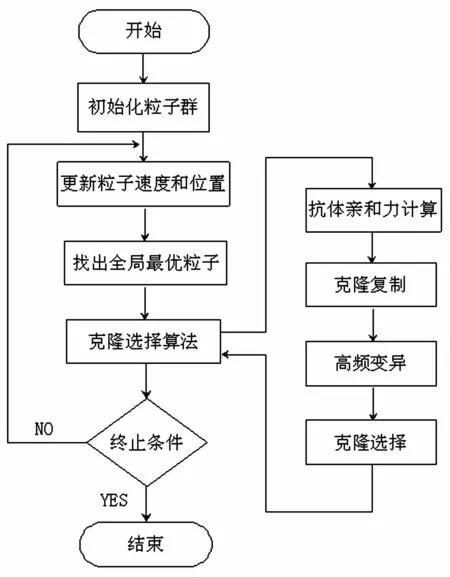
图1 实数编码克隆选择和粒子群混合算法的流程图Fig．1 RCSA-PSO flowchart

混合算法的关键步骤如下：

（1）初始化粒子。随机产生初始群体，初始化粒子的速度和位置信息。置迭代次数Iteration＝1，定义最大迭代次数MaxIter，得到相同适应度值的迭代次数Samecounter＝0。

（2）更新粒子速度和位置。计算每个粒子的适应度值，并根据粒子适应度值的大小确定个体极值pbest和全局极值gbest，依照式（1）和式（2）更新粒子位置。

（3）抗体亲和力计算。抗体亲和力是种群中抗体优良的度量标准。在克隆选择和粒子群混合算法中，将粒子视为抗体，因此抗体亲和力就等于粒子的适应度。

（4）克隆复制算子。根据抗体亲和力的大小，对亲和力高的抗体进行克隆操作。对亲和力高的前50%抗体群A，每个抗体进行一次细胞分裂，形成另一个相同的抗体群B。亲和力后50%的抗体群C保持不变。可见，该操作一方面通过克隆操作保护了优良基因，加快算法收敛速度，另一方面保留了每一个迭代步中亲和力较差的抗体，保持了群体的多样性。

（5）高频变异算子。本文中引入遗传算法中的变异算子进行高频变异操作。在个体亲和力较高的子种群A和B中引入的幅值变异算子，即以一定概率随机选取粒子中的某些维度进行小幅度的数值调整。在个体亲和力较低的子种群C中引入基因替换算子，即以一定概率随机选取粒子中的某些维度并替换为［0，1］之间的随机数。可见，幅值变异算子可以对较优的抗体在小范围进行调整，以达到局部寻优的效果；基因替换算子可对亲和力较差的抗体进行某些维度的替换，加速产生适应度更大的抗体。高频变异算子提供了产生新解的方法，使得新解的产生不受其它抗体的影响，提高了种群的多样性。

（6）克隆选择算子。抗体经过克隆复制、克隆高频变异后，如果子代个体的适应度高于其父代个体，则选择出一个适应度最高的子代个体替换对应的父代个体，将更新后的种群作为下一代个体。父代个体与子代个体的混合，避免了算法退化。

（7）比较本次迭代更新前和更新后全局最优适应度值，相等时Samecounter增加1，不相等时更新适应度值且Samecounter清零。

（8）当Samecounter达到50或者Iteration达到最大迭代次数时，终止迭代运算并输出最终结果；如不满足，转入第2步。

需要指出的是，在粒子优化和变异过程中，需添加约束保证粒子各维度的值在［0，1］范围内搜索。如果超出这一范围，则置该维度为［0，1］之间的随机数。

2 基于模态频率的目标函数

当导墙由于损伤出现裂缝时，其结构模态参数也相应发生改变。其中模态频率是实测中最易获得的模态参数，而且精度最容易保证。因此本文中选取导墙的低阶模态频率差作为智能算法寻优的目标函数。规定归一化的裂缝位置为L，归一化的裂缝长度为D，如果将L和D定义为待优化的变量，那么损伤识别问题就归结为一个有约束的非线性优化问题，其目标函数可用实测和数值模拟得出的模态频率差来表示。定义基于模态频率差的目标函数为：

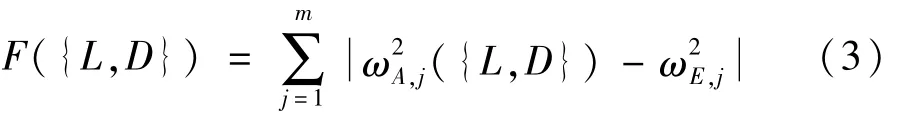
其中：m为测试模态数，下标A和E分别代表计算结果和实测结果，ωj代表结构的第j阶频率。

值得注意的是，在损伤识别过程中，不仅要追求测试信息与数值模拟结果的最优匹配，还应尽可能地找到最小程度的损伤模式。为此，引入了损伤惩罚因子，以避免由于噪声干扰等导致的损伤诊断失误。

因此，指导实测信息与数值模拟匹配的适应度函数可表示为：

其中：∑D为损伤模式对应的裂缝长度的总和；γ的取值取决于数值模型和试验数据的可信程度。可信程度越高，γ值应越小。

综上所述，该优化问题可定义为：

其中：n为结构可能产生裂缝的数目。式（5）将损伤识别问题转化为一个有约束条件的非线性最小化问题，即函数适应度值越小，匹配程度越高。

3 应用与验证

本文提出的损伤识别方法的整体思路为：在Mat-lab平台下对有限元计算软件进行二次开发，利用改进粒子群算法的寻优能力，不断更新有限元模型中损伤的位置和程度，以寻求模拟计算出的模态参数指标与实测模态参数指标的最优匹配，从而得到反映结构真实性态的有限元模型，达到准确识别结构损伤位置和程度的目的。基于智能算法优化模态频率指标的损伤识别方法的具体步骤如图2所示。

3．1 研究对象和模态阶次的选取

本文选取某水电站的中导墙作为研究对象。取两结构缝之间的24 m导墙段进行分析，导墙悬臂段高50 m。由于导墙上部悬臂部分刚度相对较小，本文将悬臂部分作为裂缝容易发生的部位进行重点分析，以验证本文所提出的新型智能损伤识别方法在环境激励下导墙结构损伤识别中的适用性。

有限元模型如图3所示，其中坐标原点选在导墙悬臂段的根部。模型采用8节点三维块体单元，利用实体楔形模拟裂缝，假定导墙悬臂段两侧均有可能产生裂缝且裂缝近似水平。模拟裂缝的长度和高度如图所示，分别利用悬臂段高度50 m和宽度24 m对裂缝位置和长度进行归一化。混凝土材料密度取2 400 kg／m3，弹性模量取35 GPa，泊松比取0．167。地基采用无质量弹性地基，弹性模量取30 GPa，泊松比取0．25。为模拟工程实际，以附加质量的形式考虑流体的影响，计算湿模态下导墙的模态频率。因为大型混凝土结构的低阶模态具有较大的振型参与系数，通常能够描述结构系统的动态特性，且结构的低阶模态参数通常较易获取并能保证足够精度，因此本文将该导墙的前6阶模态选作目标模态。不失一般性的，本文仅针对图3所示Y向振动特性进行损伤识别研究。

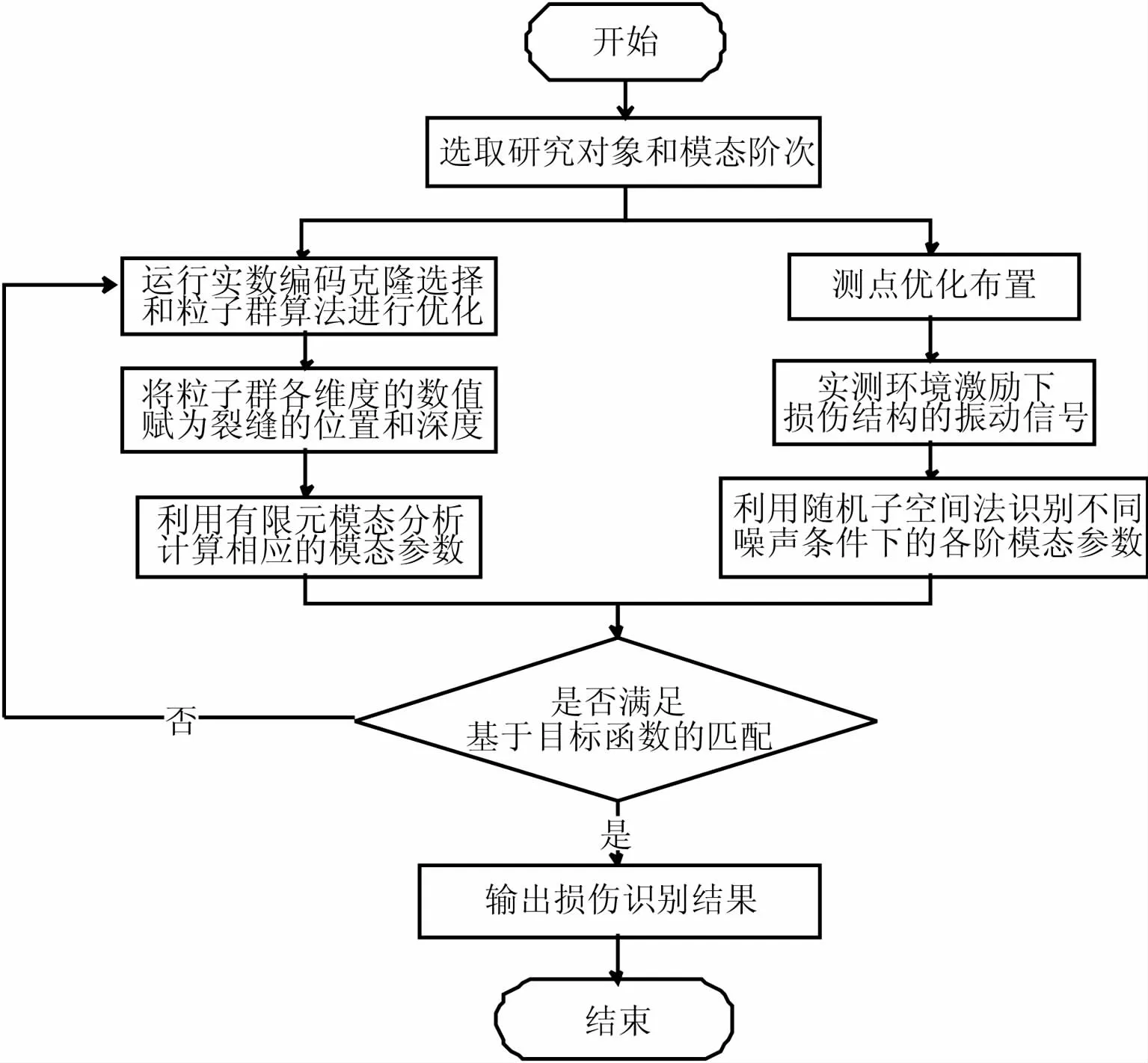
图2 本文提出的智能损伤识别方法的流程Fig．2 The procedure of the proposed method for intelligence damage identification

图3 导墙有限元模型Fig．3 FE model of the guide wall structure

3．2 考虑噪声影响的模态参数识别

本文中各损伤工况的实测信号均来自于环境激励下的有限元模拟。在有限元模拟中，以高斯白噪声作为输入（模拟环境激励），分析导墙的振动响应，其中时程信号的采样频率为100 Hz，采样时间20 s。在各测点的位移时程信号中加入白噪声数据，即：

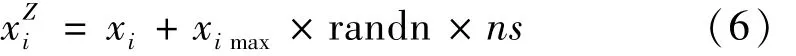
式中：xi和x分别是i测点加入噪声前后的信号，randn表示均值为零、标准差为1的高斯白噪声，ns表示时程信号中的噪声水平。因此，加入噪声的标准差为该测点时程数据最大值的ns倍。本文取ns为5%。测点可根据改进有效独立法［21－22］进行选择，这里不再赘述。

以两处裂缝损伤工况（一侧裂缝 L1＝0．7，D1＝0．2；另一侧裂缝 L2＝0．5，D2＝0．3）为例，图 4和图 5中分别为导墙结构在环境激励下添加5%白噪声时的位移时程信号图和通过现代谱方法得出的位移信号归一化的功率谱图。将识别出的前六阶模态频率作为有限元模型的匹配导向，利用智能算法搜索与实测模态信息最匹配的结构损伤模式。

3．3 方法的性能验证与比较

以噪声水平5%时，两处裂缝损伤工况（一侧裂缝L1＝0．7，D1＝0．2；另一侧裂缝 L2＝0．5，D2＝0．3）为例。经验证，损伤惩罚因子γ＝0．05时算法能获得较好的寻优效果。

假定该导墙两侧各有两处可能的损伤，则每个粒子的维度为8（包含裂缝位置维度和长度维度各4个）。运用实数编码克隆选择和粒子群混合算法结合适应度函数进行结构损伤识别。其中算法的基本参数如下：种群大小为100，c1和c2均取0．5。当算法到达最大迭代次数1 000，或者连续搜索50次最优适应度值不变时，算法终止。为了验证算法性能，选取实数编码粒子群算法（Real encoding particle swarm optimization algo-rithm，RPSO）和实数编码遗传算法（Real encoding ge-netic algorithm，RGA）与本文的新型算法进行全局寻优性能比较。其中实数编码粒子群算法的参数设置与实数编码克隆选择和粒子群混合算法一致，实数编码遗传算法的基本参数参照文献［1］中选取。针对目标函数，三种智能算法分别运行5次，典型的寻优过程如图6所示。由图6可以看出，本文中提出的实数编码克隆选择和粒子群混合算法在解决损伤识别问题的寻优效率上有明显优势，该算法的收敛速度较快，且寻优效果在三种算法中最接近理论最优解（0．025）。而实数编码粒子群算法虽然收敛也较快，但极易陷入局部最优值，寻优结果较实数编码克隆选择和粒子群混合算法有很大差距。实数编码遗传算法是一种改进遗传算法，该算法在损伤位置和程度的寻优中收敛速度较上述两种粒子群算法慢，寻优效果较实数编码粒子群算法好，但是相比实数编码克隆选择和粒子群混合算法仍有一定差距。综上所述，实数编码克隆选择和粒子群混合算法有较强的跳出局部最优的能力，在解决复杂的结构损伤识别问题时能够较快的向全局最优值逼近，是一种很有效率的全局优化算法。

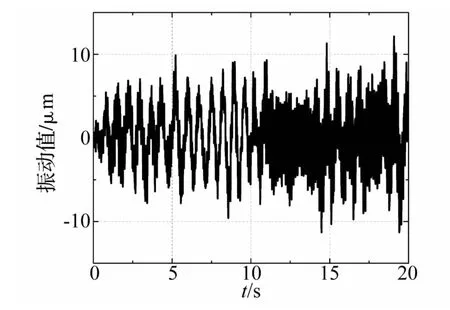
图4 典型位移时程信号图Fig．4 Time history signals of displacement

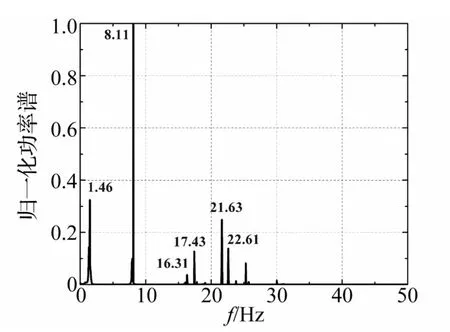
图5 位移信号的归一化功率谱图Fig．5 Normalized power spectrums of displacement

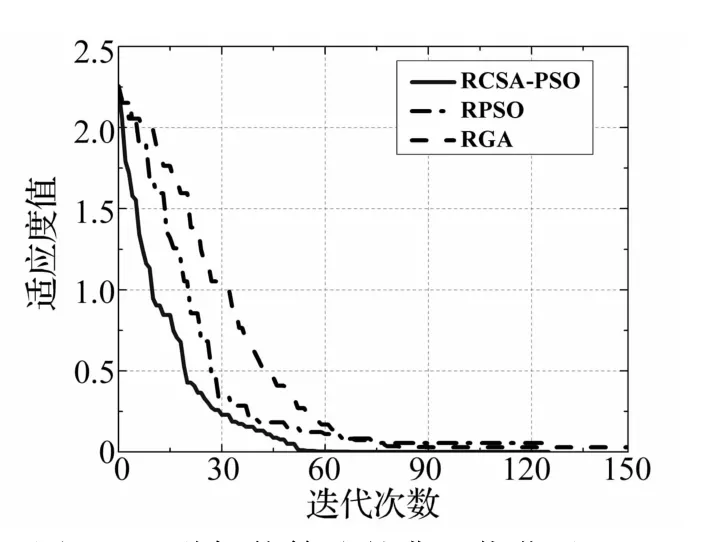
图6 三种智能算法的典型优化过程Fig．6 Fitness curves of the three intelligence algorithms

另外，从图6中还可以看出，基于模态频率的目标函数对于损伤的区分度很高，本例中的区分度约为225。本文中规定当识别出的裂缝长度小于0．03时，认为损伤对结构的影响较小，该损伤可忽略不计。利用本文的新型智能损伤识别方法能够搜索到的最匹配的损伤程度和位置和真实情况如图7所示。可见，该方法能够准确地识别出真实的结构损伤情况。

3．4 损伤识别结果

在5%噪声影响下，分别利用本文所提出的智能损伤识别方法及已有方法对一处损伤、两处损伤和多处损伤等工况进行裂缝位置和长度的识别，得到识别结果如表1所示。从表1可以看出，本文所提出的基于克隆选择和粒子群混合算法的智能损伤识别方法在5%噪声干扰下仍然能够较准确地识别出10个损伤工况下的裂缝位置和长度，证明本文提出的损伤识别方法具有一定的抗噪声能力和较高的识别精度；基于RP-SO算法的识别方法仅能识别工况1～3中一处损伤的情况，对于工况4～10中两处及以上损伤工况，由于RPSO算法易陷于局部最优值，因此识别结果的精度很低，甚至得到错误的损伤位置和程度值；基于RGA算法的识别方法在识别一处和两处损伤时较理想，对于工况7～10中两处以上的损伤情况则无法正确识别，说明RGA算法的识别能力较本文提出的混合算法有一定差距。

图7 基于本文方法的损伤识别结果Fig．7 Damage detected by the proposed method

综上所述，由于全局寻优能力的加强，本文所提出的基于RCSA－PSO算法的智能损伤识别方法对于结构损伤具有很高的识别精度，且在较复杂的损伤工况中更能体现出其优势。

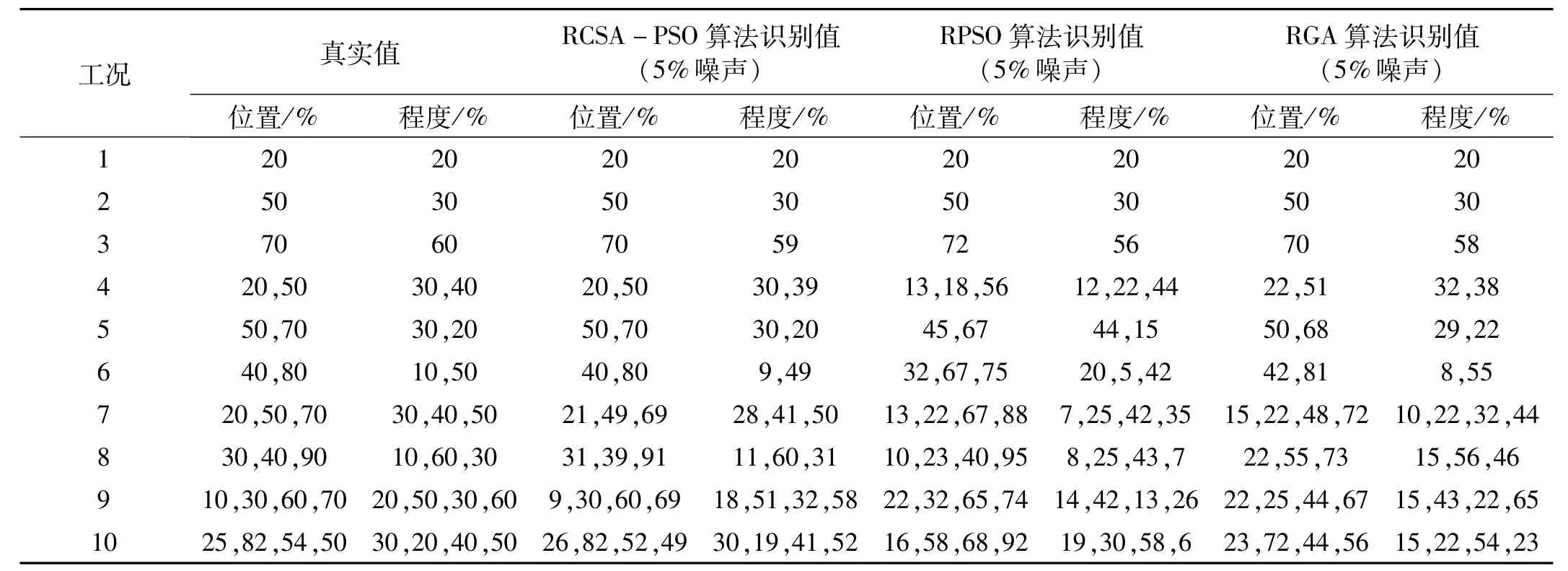
表1 损伤识别结果Tab．1 Results of damage detection

4 结 论

本文提出了一种基于实数编码克隆选择和粒子群混合算法优化模态频率指标的导墙结构智能损伤诊断方法，解决了导墙结构水下部分损伤检测难的问题。该方法仅需可测性强的低阶模态频率，且避免了神经网络和支持向量机预测时大量的样本计算和模型训练，适合于环境激励条件下的大型水工结构的无损动态损伤检测。结合在某导墙损伤识别中的应用，得到主要结论如下：

（1）经算法稳定性验证，本文提出的新型智能算法能够快速收敛于全局最优值。选取实数编码粒子群算法和实数编码遗传算法与本文的新型算法进行全局寻优性能比较，结果表明：实数编码克隆选择和粒子群混合算法收敛速度快，且有较强的跳出局部最优的能力，在解决复杂的非线性优化问题时能够较快的逼近全局最优值，是一种很有效率的全局优化算法。

（2）利用基于模态频率的适应度函数进行裂缝位置和长度的识别，结果表明：本文提出的基于模态频率的适应度函数能够准确地识别结构损伤的位置和程度，且该指标可测性较强，具有很强的实际可操作性。

（3）通过应用新型智能算法对有限元模型的参数进行优化，寻求与实际损伤结构模态频率指标的最优匹配，进而确定不同损伤工况下的损伤位置和程度。经验证表明：与现有方法相比，该智能损伤识别方法对噪声条件下各种损伤工况具有更高的识别精度，方法稳定可靠。

综上所述，本文所提出的基于实数编码克隆选择和粒子群混合算法优化模态频率指标的损伤诊断方法是十分有效的，能够准确地识别出导墙在不同损伤组合时的结构性态，可尝试在各类大型水工结构的损伤诊断中推广应用。

［1］Meruane V，Heylen W．An hybrid real genetic algorithm to detect structural damage using modal properties［J］．Mechanical Systems and Signal Processing，2011，25（5）：1559－1573．

［2］Doebling SW，Farrar CR，Prime M B．A summary review of vibration-based damage identification methods［J］．Shock and Vibration Digest，1998，30（2）：91－105．

［3］Qian J R，Ji X D，Zhang W J．Damage detection test of a substructure model of the National Swimming Center［J］．Science in China Series E：Technological Sciences，2008，51（7）：940－948．

［4］付春雨，单德山，李乔．列车行驶时桥梁结构损伤预警的时域方法［J］．振动与冲击，2011，30（1）：27－32．FU Chun-yu，SHAN De-shan，LI Qiao．Time domain method for bridge structural damage alarming when a train is running［J］．Journal of Vibration and Shock，2011，30（1）：27－32．

［5］杜永峰，李万润，李慧，等．基于时间序列分析的结构损伤识别［J］．振动与冲击，2012，31（12）：108－111．DU Yong-feng， LI Wan-run， LI Hui， et al． Structural damage identification based on time series analysis［J］．Journal of Vibration and Shock，2012，31（12）：108－111．

［6］ El-Ouafi Bahlous S，Smaoui H，El-Borgi S．Experimental validation of an ambient vibration-based multiple damage identification method using statistic al modal filtering［J］．Journal of Sound and Vibration，2009，325：49－68．

［7］常军，任永辉，陈忠汉．环境激励下结构损伤识别的综合指标法试验研究［J］．工程力学，2011，28（7）：130－135．CHANG Jun， REN Yong-hui， CHEN Zhong-han．Experimental investigation of structural damage identification by combination index method under ambient excitation［J］．Engineering Mechanics，2011，28（7）：130－135．

［8］练继建，张建伟，王海军．基于泄流响应的导墙损伤诊断研究［J］．水力发电学报，2008，39（1）：96－101．LIAN Ji-jian，ZHANG Jian-wei，WANG Hai-jun．Study on damage diagnosis of guide wall based on flood discharge response［J］．Journal of Hydroelectric Engineering，2008，39（1）：96－101．

［9］练继建，崔广涛，黄锦林．导墙结构的流激振动研究［J］．水利学报，1998，11：33－37．LIAN Ji-jian，CUIGuang-tao，HUANGJin-lin．Study on flow induced vibration of spillway guide wall［J］．Journal of Hydraulic Engineering，1998，11：33－37．

［10］练继建，李松辉．基于支持向量机和模态参数识别的导墙结构损伤诊断研究［J］．水利学报，2008，39（6）：652－658．LIAN Ji-jian，LI Song-hui．Damage diagnosis of spillway guide wall based on support vector machine and modal parameter identification ［J］． Journal of Hydraulic Engineering，2008，39（6）：652－658．

［11］李松辉．基于机器学习和模态参数识别理论的水工结构损伤诊断方法研究［D］．天津：天津大学，2008．

［12］熊仲明，王超，林涛．基于神经网络的大跨钢结构缺陷损伤的定位研究［J］．振动与冲击，2011，30（9）：191－196．XIONG Zhong-ming， WANG Chao， LIN Tao． Defect determination of large-span steel structure based on neural network［J］．Journal of Vibration and Shock，2011，30（9）：191－196．

［13］Song H Z，Zhong L，Han B．Structural damage detection by integrating independent component analysis and support vector machine［J］．International Journal of Systems Science，2006，37（13）：961－967．

［14］ He R，Hwang S．Damage detection by an adaptive real-parameter simulated annealing genetic algorithm ［J］．Computers and Structures，2006，84（31－32）：2231－2243．

［15］ Vakil-Baghmisheh M，Peimani M，Sadeghi M H，et al．Crack detection in beam-like structures using genetic algorithms［J］．Applied Soft Computing，2008，8（2）：1150－1160．

［16］Kennedy J，Eberhart R C．Particle swarm optimization［C］．In：Proc IEEE Conf on Neural Networks，Perth，1995：1942－1948．

［17］练继建，何龙军，王海军．基于PSO优化LS-SVM算法的水电站厂房结构振动响应预测［J］．中国工程科学，2011，13（12）：45－50．LIAN Ji-jian，HE Long-jun，WANG Hai-jun．Prediction of vibration response of powerhouse structures based on LS-SVM optimized by PSO［J］．Engineering Sciences，2011，13（12）：45－50．

［18］王星星，吴贞焕，杨国安，等．基于改进粒子群算法的最小二乘影响系数法的理论及实验研究［J］．振动与冲击，2013，32（8）：100－104．WANG Xing-xing，WU Zhen-huan，YANG Guo-an，et al．Theory and tests fo least square influence coefficient method based on an improved particle swarm optimization algorithm［J］．Journal of Vibration and Shock，2013，32（8）：100－104．

［19］Burnet F M．The clonal selection theory of acquired immunity［M］．Cambridge：Cambridge University Press，1959．

［20］De Castro L N，Von Zuben F J．Learning and optimization using the clonal selection principle［C］．IEEE Transactions on Evolutionary Computation，Special Issue on Artificial Immune Systems，2002，6（3）：239 251．

［21］Lian J J，He L J，Wang H J．Optimal sensor placement in hydropower house based on improved triaxial Effective Independence method［J］．Water Science and Engineering，2012，5（3）：329－339．

［22］何龙军，练继建，马斌，等．基于距离系数－有效独立法的大型空间结构传感器优化布置［J］．振动与冲击，2013，32（16）：13－18．HE Long-jun，LIAN Ji-jian，MA Bin，et al．Optimal sensor placement for large space structures based on distance coefficient-effective independence method［J］．Journal of Vibration and Shock，2013，32（16）：13－18．