基于拉普拉斯权重的低速重载设备声发射信号趋势分析

黎 敏，王晓景，阳建宏

（北京科技大学 机械工程学院，北京 100083）

趋势分析是设备状态监测与故障诊断中的一个重要环节。通常是对设备的特征参数进行连续监测，然后根据所得到的数据判断设备当前的运行状态，并对设备将来的运行状态做出估计，进一步预报设备的剩余寿命，这对设备维修决策的制定具有重要的意义。

对于低速重载的滚动轴承，声发射技术相对于传统的振动检测具有发现早期故障的能力，可以为设备的安全、稳定、长周期、满负荷优质运行提供有力保障［1］。但声发射信号的特征量主要有计数、能量、ASL等多个特征［2－3］。不同的特征量具有不同的物理含义，且对故障的敏感程度也不同，即某些特征量能够在故障早期发生相应的突变，而一些特征量的变化趋势平缓，无法为设备的故障状态提供预警。因此，需要针对低速重载设备的声发射信号进行特征选择。

特征选择是指在m个特征量中选出d个最能反映样本属性的特征（d＜m）［4］，其本质是一个组合优化问题，而求解组合优化问题最直接的方法就是搜索。理论上，可以通过穷举法来搜索所有可能的特征组合，以评价标准最优的特征子集作为最后的输出。但是，m个特征的搜索空间为2m！。穷举法的运算量随着特征个数的增加而呈指数递增，实际应用中经常碰到几十甚至上百个特征，因此穷举法虽然简单却难以实际应用。最常用的特征选择方法是直接用分类器的分类错误率来作为对特征子集优劣性的评价指标，即特征选择与分类器是相互关联的，因此称为“封装型”特征选择方法［5－6］。该类方法直接利用分类器的分类性能来评价特征子集的优劣。当固定分类器后，所找到的特征子集分类性能通常更好。但是，该方法选出的特征通用性不强，当改变分类器时，需要针对该分类器重新进行特征选择；此外，由于每次对特征子集的评价都要进行分类器的训练和测试，所以算法计算复杂度高，尤其对于大规模数据集而言，算法的执行时间更长。

为了减少特征选择过程受分类器性能的影响，发展了“过滤型”特征选择方法［7］。该方法的特点在于只利用数据本身的内在性质来决定哪些特征应该保留，哪些特征应该被删除，而不依赖于分类器的选择。方差是最简单的一种特征选择方法，一个特征的方差越大，说明该特征表征样本的能力越强，越能够说明样本的分布。因此，往往在m个特征中，按照方差大小，降序排列，来选择前d个方差最大的特征作为选择的结果。但是，方差不能体现样本的聚类信息。Dash等［8］提出了一种称为距离熵的度量，距离熵越小，数据点的聚类效果越好，采用该度量方法对特征进行排序，可以有效去除不相关的特征。He等［9］结合特征量的方差信息和样本的聚类特性，提出了拉普拉斯权重方法来进行特征的选择，使特征对样本具有更好的可区分度。本文利用拉普拉斯权重法对声发射的各特征量进行分析，得到衡量各特征量重要性的权重值；然后，将权重与对应的特征量进行线性加和，融合得到一个能反映设备状态的综合指标；最后，利用该综合指标对低速重载轴承进行趋势分析。通过工业现场高炉皮带轴承的声发射数据，验证了新方法的有效性。

1 基于拉普拉斯权重的趋势分析方法原理

拉普拉斯权重方法是以拉普拉斯映射为基础，基于一个基本假设而展开研究的，即高维空间中邻近的点，在低维空间依然保持邻近关系，并且任一数据点均可由其邻域内的其他数据点来线性表示［10］。假设在低维空间中的数据点可以表示为：

其中：数据点xi由k个邻近点的线性组合来表示，Wij为数据点xi与这k个邻近点间的距离。

在式（1）的基础上，通过核函数的变换，将低维空间中的数据点映射到高维空间中，则在高维空间中的点可以用式（2）来表示，其中φ（·）为核函数：

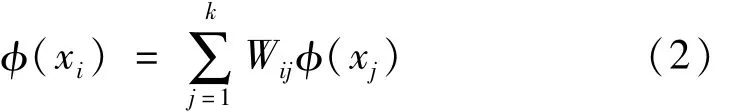
无论是在低维空间还是在高维空间中，由于数据点间存在相互依存的关系，可以将数据点分别向每个特征方向投影，若该特征方向依然能保持数据点间的邻近关系，则说明该特征方向是可以刻画数据内部性质的合适特征。

综上所述，评价一个特征的优劣，主要是考察该特征能否反映样本的局部保持特性，本质上是要求特征能反映样本的聚类特性，如图1所示。特征F1可以完全区分出两类样本，而样本在特征F2上则难以被正确识别。由此可见，特征选择的关键就是要找出能够反映样本在空间分布的特征。

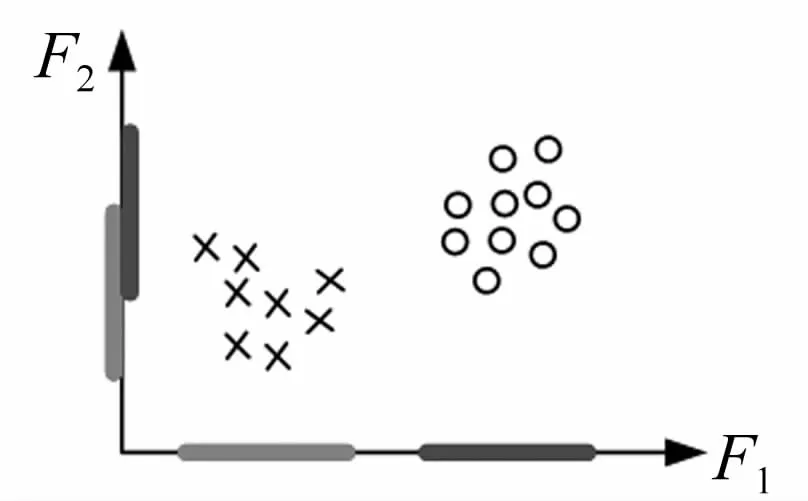
图1 特征选择的示意图Fig．1 Sketch of feature selection

根据上述思想，拉普拉斯权重方法首先构建样本的邻接图，再对图中每条边赋予不同的权重大小，并在此基础上，设计特征评价指标，该指标的值越小，说明特征越能反映样本的聚类特性，则该特征越重要。具体计算过程如下。

1．1 构建邻接图G

设有样本集Xn×m，其中n表示样本个数，m表示特征维数。计算每个样本点xi与其它样本点间的欧式距离。当xj是xi最近的k个邻近点中的一个，则邻接图G中xixj就有一条边存在，设为Gij＝1。反之，xj不是xi的邻近点，则Gij＝0。通过构建邻接图，可以确定样本集中各点之间的邻近关系。

1．2 计算邻接权重

当Gij＝1，利用热核法（Heat kernel）来确定该边的权重：

式中：t为常量，权重Wij是一个指数衰减的函数，即：若两点靠得越近，则Wij值越大，其取值范围是0＜Wij1。该权重Wij表示各点之间的靠近程度。当Gij＝0，则权重Wij＝0。利用两点之间的邻接权重作为惩罚因子，对靠得近的点赋予更大的权重，而离得远的点则被进行惩罚，使得权值很小。这样使得样本具有更好的可区分性。

1．3 特征评价指标

为了保持样本点之间的局部特性，就要让G中有边连接的点都尽可能地靠在一起，则要使得下面的目标函数达到最小，即：

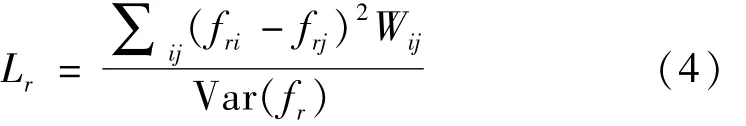
式（4）中的分母部分 Var（fr）表示特征的方差，该值越大，说明第r个特征对样本的表示能力越强；而分子部分∑ij（fri－frj）2Wij则主要是度量样本在第 r个特征上的分布情况，其中fri表示第i个样本的第r个特征值，frj表示第j个样本的第r个特征值。由此可以看出，fri和frj表示的是同一个特征值下的不同样本。此时，期望特征差（fri－frj）2会越小越好，这样就能越能反映样本的靠近程度。综上所述，分母部分希望越大越好，而分子部分则越小越好，因此特征评价指标Lr越小，则对应的第r个特征就越能刻画样本的聚类特性，该特征越重要。

1．4 趋势分析的新特征

声发射不同的特征量对故障的敏感程度也不同，利用拉普拉斯权重法对各个特征的重要性进行排序，以特征评价指标1／Lr作为系数，融合成一个新的特征LA，即：

其中：1／Lr表示第r个特征的权重，该特征越重要，则权重值越大。由于新的特征LA融合了n个声发射的特征量，不仅能够全面反映出声发射产生的物理过程，而且能突出关键特征量的作用，因此能更好地刻画设备状态的劣化趋势，也避免了由于特征选择不合适对趋势分析结果带来的影响。基于拉普拉斯权重的趋势分析方法的具体计算流程如图2所示。

图2 基于拉普拉斯权重的趋势分析方法流程图Fig．2 Flow diagram of trend analysis method based on Laplacian score

2 低速重载轴承的趋势分析

为验证基于拉普拉斯权重的趋势分析方法的有效性，以低速重载轴承为对象进行实验分析。高炉皮带是冶炼生产的关键设备，处于整个高炉的“咽喉”部位，其所在的位置如图3所示。如果皮带的任意一个元件出现故障，都会造成皮带的非正常工作，使得整个炼钢系统将趋于瘫痪。以4中编号为6的张紧改向滚筒的轴承为测试对象，分别命名为轴承1和轴承2，现场位置如图5所示。张紧改向滚筒两端的支撑轴承由于转速低（60 r／min）、负载重（皮带的堆比重为 2 000 kg／m3），常出现疲劳磨损、胶合等严重故障，其运行状态的好坏，直接影响着高炉的正常生产。

图3 高炉皮带的位置Fig．3 Location of belt in the blast furnace

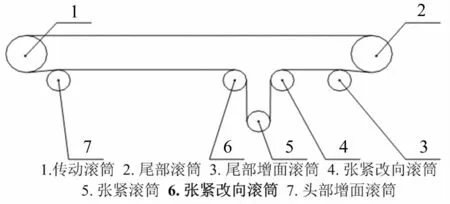
图4 高炉带结构简图Fig．4 Structural sketch of belt in the blast furnace

图5 轴承位置示意图Fig．5 Location of the bearings

两轴承于2009年4月更换过一次，原因是内圈和外圈存在多处严重的点蚀故障，最大的坑径达到10 mm×20 mm。经过4年的满负荷运行，在2013年3月初发现轴承又出现了异常振动的情况，随即展开了周期监测。利用美国PAC公司的多通道声发射检测设备对轴承进行数据采集，参数如表1所示。

表1 声发射采集参数Tab．1 Acquisition parameters of acoustic emission

根据拉普拉斯权重法的原理，要对声发射的各个特征量的重要性进行准确评价，首先需要对带标签的样本数据进行分析。在这里，取2009年4月轴承1解体前后的数据进行特征重要性的排序。采集到的原始声发射数据如图6所示，其中图6（a）表示轴承1解体前的故障状态数据，而图6（b）则表示轴承1正常状态下的数据。

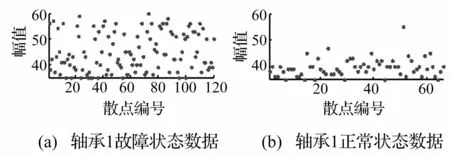
图6 用于特征重要性分析的声发射原始数据Fig．6 The acoustic emission data used for feature importance analysis

通常将图6中所示的每个数据点称为一个声发射事件，也称为散点。在相同的采集时间150 s，相同的门槛值35 dB的情况下，滚动轴承的故障越严重，则声发射事件数就越多。每个声发射事件都对应着一个4K的声发射波形，由每个波形数据可以计算出如下9个特征值：上升时间、计数、能量、持续时间、幅值、RMS、ASL、信号强度、绝对能量。因此，可以将每个声发射事件作为一个样本，每个样本用9个特征量来描述。于是，参与计算分析的故障数据为120×9的样本矩阵，正常数据则为80×9的样本矩阵。对声发射各特征量的重要性评价结果如表2所示。

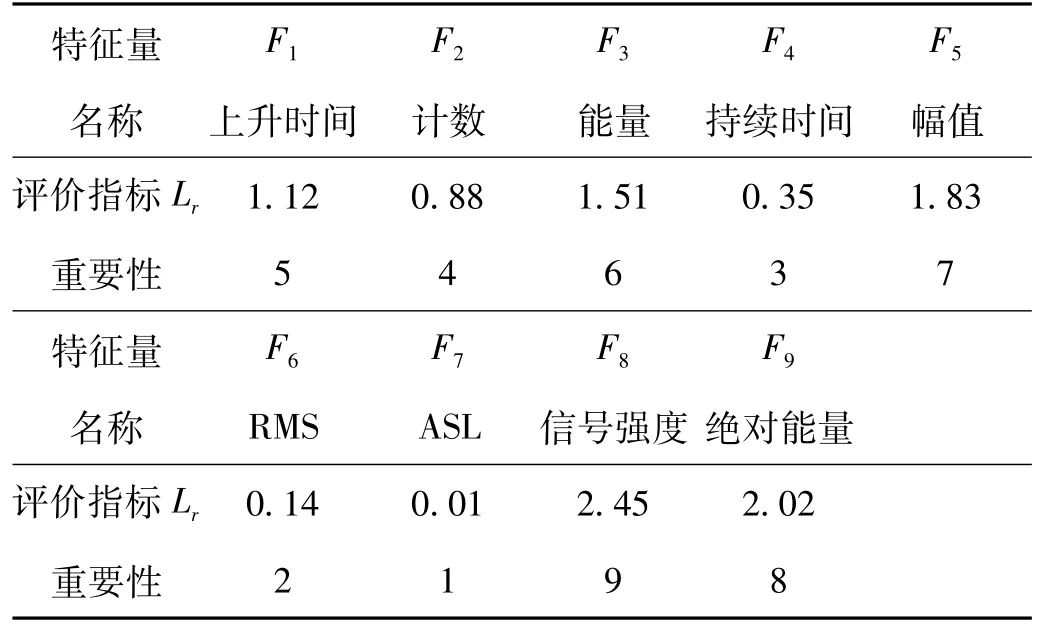
表2 声发射各特征量的评价结果Tab．2 Evaluation results of acoustic emission features

从表2中可以看出，F7特征量ASL（电平均值）的特征评价指标值最小，说明该特征最重要；而F8信号强度的特征评价指标值最大，则该特征的重要程度最低。根据式（5）对各特征量进行融合，可以得到一个新的特征LA，以此来描述2013年3月轴承出现异常振动后的劣化趋势。采集到的声发射原始数据如图7所示。

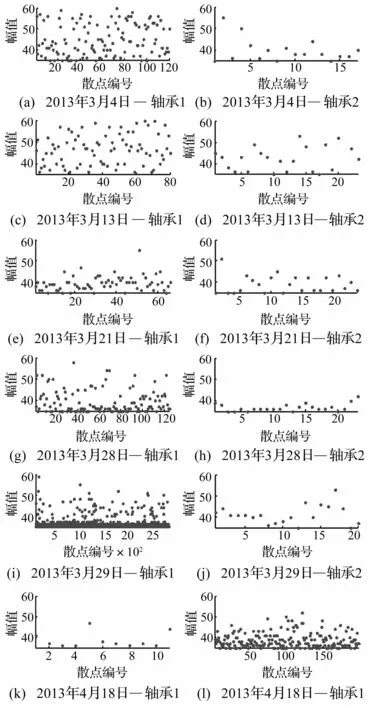
图7 声发射采集的原始数据Fig．7 The original acoustic emission data

在工业现场，于2013年4月1日更换了轴承1，但受到工艺检修时间的限制，未对轴承2进行更换。从图7中的整体趋势上可以定性地看出，轴承1随着故障严重程度的增加，声发射事件数也不断增加；当轴承1更换后，其声发射事件数则明显减少。而对于轴承2而言，前期变化不大，当更换了轴承1后，其状态劣化的程度变得较为明显。为做到定量分析，分别以表2中所列出的9个常用声发射特征量来分别进行趋势分析，结果如图8所示。

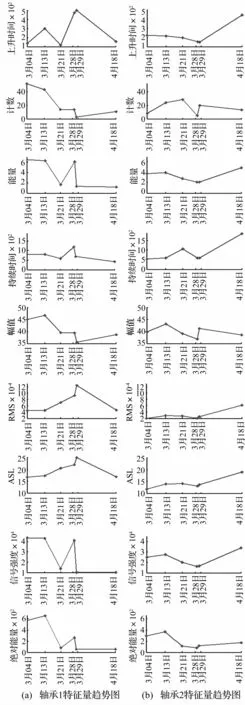
图8 利用声发射常用特征量进行趋势分析Fig．8 Trend analysis of common acoustic emission features

需要说明的是，每个特征量趋势图中都有6个数据点，分别代表了在2013年3月4日～2013年4月18日的时间段内对轴承1和轴承2进行的6次数据采集，每个数据点是对每次采集到的声发射数据进行特征值平均处理后所得到的。

从图8中可以看出，仅有RMS和ASL两个特征能够准确反映出该轴承的劣化趋势，而其他的七个特征则无法有效刻画轴承的趋势变化。由此可以看出，特征选择的正确与否直接影响了趋势分析的正确性。因此，需要综合考虑各个特征量的作用，利用新特征LA来综合评价轴承的劣化趋势，结果如图9所示。

图9 新特征LA的趋势分析Fig．9 Trend analysis of new feature LA

从图9中可以看出，直至3月29日，随着轴承1故障程度的不断加重，新特征LA一直处于上升趋势，在更换了轴承1后，于4月18日的测试数据中，新特征LA则回落到正常水平。由此可以看出，新特征LA可以反映轴承1的劣化趋势，克服了由于特征选择不正确所带来的影响。经现场拆卸验证，轴承1的外圈和滚动体存在明显的压痕，如图10所示。

图10 轴承1拆卸后的现场实物图Fig．10 Actual picture of disassembled bearing No．1

对于轴承2而言，在3月29日轴承1处于故障最严重的时候，轴承2的故障程度确实相对较低，无需更换。而在4月18日的测试数据中，新特征LA处于上扬的趋势，从一个动力学系统的角度来分析，当轴承1出现故障时，轴承2也不可避免地存在故障，只是故障的严重程度不同而已。目前只更换了系统中的轴承1，而对于同样满负荷运行的轴承2并未更换，在载荷、温度、速度等工况参数不变的情况下，轴承2势必将处于持续劣化的状态。由此可以看出，新特征LA可以反映出轴承2状态的变化，可为现场点检人员提供数据参考，需重点关注轴承2的劣化趋势，并制定合理的维修决策。

3 结 论

（1）拉普拉斯权重法同时考虑了特征量的方差信息和样本的聚类特性，得到特征评价指标Lr，该指标的值越小，说明特征越能反映样本的分布特性，则特征越重要。

（2）由于声发射信号的特征量多，且对故障敏感程度不同，利用拉普拉斯权重法可对声发射各个特征量进行重要性的排序，并以此作为权重系数，将多个特征量融合成一个新的特征LA，即可以全面反映声发射产生过程的物理现象，又能突出关键特征量的作用。

（3）提出基于拉普拉斯权重的声发射信号趋势分析方法，并将其应用在低速重载轴承的趋势分析中。实验结果表明，新特征LA可以有效地反映出轴承的劣化趋势，无需再在繁多的特征量中进行选择，克服了由于特征选择的不正确对趋势分析结果带来的影响。此外，新特征LA对故障严重程度较敏感，可有效区分出轴承所处不同的故障状态，为现场点检维修提供必要的数据参考。

［1］郝如江，卢文秀，褚福磊，等．声发射检测技术用于滚动轴承故障诊断的研究综述［J］．振动与冲击，2008，27（3）：75－79．HAO Ru-jiang，LU Wen-xiu，CHU Fu-lei，et al．Review of diagnosis of rolling element bearings defaults by means of acoustic emission technique［J］．Journal of Vibration and Shock，2008，27（3）：75－79．

［2］聂志军，高立新，胥永刚，等．低速重载设备声发射技术检测的现状与发展［J］．机械设计与制造，2008（7）：220－222．NIE Zhi-jun， GAO Li-xin， XU Yong-gang， et al． The present status and development of AE detect in low-speed heavy load equipment ［J］． Machinery Design and Manufacture，2008（7）：220－222．

［3］李修文，阳建宏，黎敏，等．基于频域形态滤波的低速滚动轴承声发射信号降噪新方法［J］．振动与冲击，2013，32（1）：65－68．LI Xiu-wen，YANG Jian-hong，LI Min，et al．A new de-noising method for acoustic emission signal of rolling bearings with low speed based on morphological［J］．Journal of Vibration and Shock，2013，32（1）：65－68．

［4］边肇棋，张学工．模式识别第2版［M］．北京：清华大学出版社，2000．

［5］John G H，Kohavi R，Pfleger K．Irrelevant features and the subset selection problem［C］．Proceedings of the Eleventh International Conference on Machine Learning，1994，129：121－129．

［6］Sun Z H，Bebis G，Miller R．Object detection using feature subset selection［J］．Pattern Recognition，2004，37（11）：2165－2176．

［7］Dash M，Liu H．Feature selection for classification［J］．International Journal of Intelligent Data Analysis，1997，1（3）：131－156．

［8］Dash M，Choi K，Scheuermann P，et al．Feature selection for clustering-a filter solution［C］．Proceedings of 2002 IEEE International Conference on Data Mining．2002：115－122．

［9］HE Xiao-fei，CAI Deng，Niyogi P．Laplacian score for feature selection［R］．Advances in Neural Information Processing Systems，2006，17，MIT Press，Cambrigde，MA．

［10］Belkin M，Niyogi P．Laplacian eigenmaps and spectral techniques for embedding and clustering［J］．Advances in Neural Information Processing Systems，2002，14：585－591．