火箭飞行姿态的可视化绘制方法*

淡 鹏，王 丹，侯黎强，马 宏

（1宇航动力学国家重点实验室，西安 710043;2西安卫星测控中心，西安 710043）

0 引言

在运载火箭（或导弹）的三维飞行视景可视化绘制中，为了更加真实地反映飞行过程中火箭与飞行速度、地平面、太阳等目标或矢量之间的关系，以及对火箭大角度调姿、火箭起旋过程等进行真实感展示，就需要对其飞行姿态数据进行可视化绘制。为此，文中基于OpenGL图形库和Visual C++编程技术，对姿态的获取及绘制方法进行了研究与实现。

1 火箭姿态常用参考坐标系

火箭飞行过程可视化的常用参考坐标系有以下几种:

1）发射系与发射惯性系:发射系坐标原点与发射点固连，OX轴在发射点水平面内并指向发射瞄准方向，OY轴垂直于发射点水平面指向上方，OZ轴为右手法则确定的方向。发射惯性系起飞瞬时与发射系重合，起飞后原点及各轴在惯性空间保持不动。

2）箭体坐标系:箭体坐标系［1－2］为火箭固连坐标系，随火箭一起运动，其原点为火箭质心，X轴沿着火箭体轴方向，并指向火箭的头部，Y轴在火箭纵对称面内，垂直于纵轴，指向第Ⅲ象限。

3）DX-2地心固联坐标系:DX-2地心固联坐标系（简称地固系），其坐标原点在地球质心，X轴在真赤道面内指向零子午圈;Z轴指向国际习用原点（CIO）;Y轴与Z轴、X轴垂直构成右手坐标系。

4）J2000地心惯性系:J2000平春分点平赤道地心惯性系，其坐标原点为地球质心，基本平面为J2000.0地球平赤道面，X轴在基本平面内由原点指向历元平春分点，Z轴过坐标原点指向北极，Y轴由右手规则确定。

2 姿态数据获取与处理方法

火箭姿态确定所用数据来自于火箭遥测，由于火箭飞行制导系统测量坐标系建立在惯性坐标系下，因而从火箭遥测获取的姿态参数一般为发射惯性系下的数据（有时为姿态导航系，可通过平移变换到发射惯性系）。根据火箭类型不同，其姿态参数传输的类型与个数也可能不同，具体可使用箭遥姿态数据中的姿态程序角、姿态角偏差以及火箭飞行的理论姿态角等综合计算出当前历元时刻的姿态角（俯仰角、偏航角、滚动角）数据［2］（需要根据箭遥参数种类等进行取舍）。

当有程序角与姿态角偏差时，可使用程序角加上偏差的方法得到当前姿态角，用公式表示为:

姿态角=程序角+姿态角偏差

当只有姿态角偏差时，可使用理论姿态角与偏差相加的方法得到当前姿态角，用公式表示为:

姿态角=理论姿态角+姿态角偏差

在对姿态数据的三维绘制过程中，当需要使用实测姿态数据时，由于姿态测量系统不可避免的存在各种噪声及野值数据，就必须对所取得的欧拉角参数进行平滑与剔野处理，以免显示过程中箭体方向出现较大幅度抖动。

关于火箭姿态野值的剔除问题，此类方法较多，常用的方法有合理范围法、差分检测法和多项式外推残差判断法等。合理范围法就是给定角度α的一个合理范围时认为是野值。差分检测法通过对前后两点角度进行差分来计算角度变化率，当变化率不满足给定阀值时认为是野值，也可进一步通过判断变化率的变化率进行更严格的限制。

多项式外推残差判断法需要对多点角度数据进行多项式拟合计算，如采用二次或三次多项式，其构造方法常用有最小二乘拟合法、样条函数法、拉格朗日插值法等。以最小二乘二次多项式为例，设角度α对时标t的拟合多项式为α=at2+bt+c（其中，a、b、c为待估系数），通过将多点测量值代入解算函数极值的方法可解算出系数，进而可估计出t时刻的估计值，当t时刻测量值αt与估计值差，以及门限值δ满足δ时，认为 αt为正常值，被接受，否则使用估计值代替αt。

需要注意的是，上面这几种方法使用中需要合理选择剔野的门限值。另外在姿态平滑及剔野中使用较多的是卡尔曼滤波方法，此类算法较多，如文献［3］给出的弱机动及强机动状态下的姿态EKF滤波算法，文献［4］给出的状态切换UKF滤波姿态确定算法，文献［5］使用的QCDKF算法等。

3 姿态三维绘制方法

火箭或导弹飞行过程三维绘制［6－7］时，主要涉及位置及姿态的绘制，当保持基准坐标系不动时，可先将火箭3D模型加载到视场中后，根据姿态数据进行模型旋转，然后再平移到火箭所在位置。

在火箭位置及姿态绘制中常采用地心固连系或J2000地心惯性系作为基本参考系（由于惯性系坐标与时间相关，故更多的使用地固系），对于地固系下位置矢量recf与J2000惯性系下位置矢量reci，两者间的转换关系为:

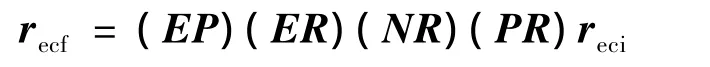
其中:PR为岁差矩阵，NR为章动矩阵，ER为地球自转矩阵，EP为极移矩阵。

考虑到火箭三维绘制中不需要过多精确的计算，则对于这两者之间的转换，可只考虑ER自转矩阵，即只考虑当前时刻的格林尼治恒星时角的差别。此时在三维绘制中，地心惯性系到固连系之间可通过绕Z轴旋转一个恒星时角的方法实现。

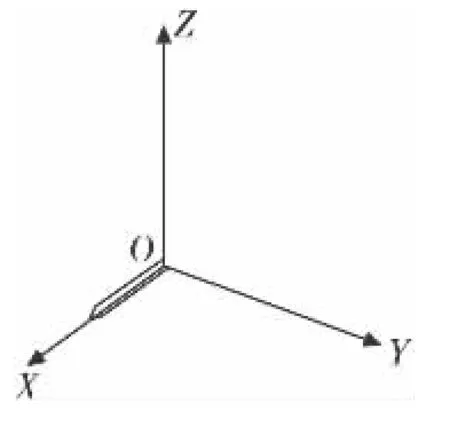
图1 火箭在姿态参考系的初始指向

火箭位置显示比较简单，下面只探讨姿态的绘制方法。设不考虑火箭位置的情况下，火箭模型加载到视景中的初始方向沿着姿态参考系的X轴方向（如图1所示，由于模型视图变换方法多样，此参考系X轴与OpenGL的世界坐标系X轴可能不同）。此时，姿态的三维绘制可通过下面介绍的几种方法进行实现。

3.1 多次旋转法

将火箭飞行T时刻发射惯性系3个欧拉角记为俯仰角φ、偏航角ψ、滚动角γ，发射系下对应欧拉角分别记为 φf、ψf、γf，设此欧拉角遵循 3-2-1 转序。起飞时间记为T0，发射方位角为A，发射工位地理经度记为λ，地理纬度为δ，起飞时刻发射工位格林尼治恒星时角记为ST0，则其赤经为α=λ+ST0，赤纬为β（可用δ近似）。

图2 地固到发惯的旋转关系

当使用地固系作为参考系时，一种较直观的姿态可视化方法是借助OpenGL提供的强大的三维坐标旋转功能，先将地固系下的火箭初始模型根据发射工位的天文坐标（三维绘制中可使用大地经度、大地纬度近似）及发射方位角（或称为射向）旋转到发射惯性系下。

设在T时刻（T为相对T0的时间）发射惯性系下的发射工位在地球固连系下经度为λ－wT（w为地球自转角速度）。则旋转方法为:1）绕Z轴旋转λwT;2）绕Y轴旋转 －δ－π/2;3）绕X轴旋转 －π/2;4）绕Y轴旋转A。用公式可表示为:

然后再根据当前姿态的欧拉角旋转到箭体坐标系下，对3-2-1转序来说，其旋转方法为:1）绕Z轴旋转φ;2）绕Y轴旋转ψ;3）绕X轴旋转γ。用公式可表示为:RX（γ）RY（ψ）RZ（φ）。

当以地心惯性系作为参考系时，发惯系工位起飞时刻在地惯系下赤经为α=λ+ST0，多次旋转方法与上面地固系多次旋转仅在第一步不同，改为绕Z轴旋转α角即可。

整个旋转过程用OpenGL语句表示为:

3.2 将姿态角转换到地固系或地惯系

常用的火箭姿态以发惯系（或发射系）作为参考系，为了方便三维显示的使用，也可直接将姿态参考系建立在地固系或地惯系下。此时的3个欧拉角为地固（或地惯）到箭体坐标系的旋转角度，设3-2-1转序下3个旋转角为:绕Z轴转角为ψ，绕Y轴转角为θ，绕X轴转角为φ（此处3个欧拉角无明显的滚动、俯仰、偏航含义，故此处称为绕某轴的转角）。则此时参考系到箭体系的转换矩阵M为:

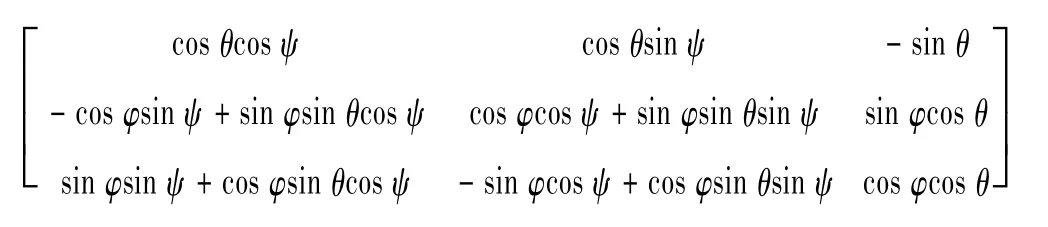
若能计算出M，则可据此解算出3个转角:

绕 Z 轴转角为 ψ =arctan2（M（1，2），M（1，1））

绕Y轴转角为θ=arcsin（－M（1，3））

绕 X 轴转角为 φ =arctan2（M（2，3），M（3，3））

需要说明的是，上面式子中借助了VC编程中的反正切函数arctan 2进行表示。

而根据火箭姿态角，可得到发惯系到箭体系转换矩阵Mfb，又由参考系到发惯系的旋转关系可得到参考系到发惯系的旋转矩阵Mcf，则参考系到箭体系转换矩阵为M=McfMfb。

这样就可计算出地固或地惯参考系下的欧拉转角，即可方便的实现姿态数据的绘制。此算法的旋转过程用 OpenGL语句表示为:glRotatef（ψ，0.0f，0.0f，1.0f）;glRotatef（θ，0.0f，1.0f，0.0f）;glRotatef（φ ，1.0f，0.0f，0.0f）;

3.3 不考虑滚动时的赤经赤纬方法

如不需要考虑火箭的滚动角度，则对姿态的绘制也可通过计算火箭纵轴方向在地惯系下的赤经、赤纬的方式来实现。

由火箭的俯仰角φ、偏航角ψ、滚动角γ，可得到火箭纵对称轴在发射惯性系下的矢量方向为X=（cosφcosψ，sinφcosψ，－sinψ），又由T0时刻发射工位的赤经可计算出地惯系到发惯系的转换矩阵M，则火箭纵对称轴在地惯系的方向矢量为XI=MX。即可解算出纵对称轴的赤经为α =arctan（XI［2］/XI［1］），赤纬为 β =arcsin（XI［3］）。

此时，火箭体轴方向在J2000地心惯性系下的绘制可通过两次旋转得到:1）绕Z轴旋转α角;2）绕Y轴旋转β角。

这两次旋转用OpenGL语句表示为:

glRotatef（α ，0.0f，0.0f，1.0f）;

glRotatef（β ，0.0f，1.0f，0.0f）;

对地固系参考系，将赤经、赤纬替换为火箭纵对称轴的地心经度、地心纬度即可。其地心经度为λ=α－ST（ST为当前时刻的格林尼治恒星时角），地心纬度可用β近似。

图3 原型软件对火箭飞行绘制效果

4 应用效果

采用VC++开发工具及OpenGL图形库进行了火箭飞行过程视景显示系统的原型软件实现，飞行过程的可视化效果如图3所示。

5 结束语

文中总结了火箭姿态数据的获取及计算方法，给出了其可视化绘制的三种方法，并使用文中方法对火箭飞行过程进行了绘制实现，取得了较好的可视化效果，证明了方法的可行性。应该看到，文中给出的三种火箭姿态绘制方法各有优缺点:方法1不需要做复杂的计算，可直接使用发惯系的姿态角;方法2需要将姿态角转换为地固系转角;方法3只需两次旋转即可完成变换，但没有考虑滚动角。实际使用中可根据情况灵活选择。

［1］王志刚，施志佳.远程火箭与卫星轨道力学基础［M］.西安:西北工业大学出版社，2006.

［2］王玉祥，张忠华，何剑伟.用箭遥数据计算三轴稳定卫星初始姿态［J］.遥测遥控，2007，9（5）:65－68.

［3］张凯，单甘霖，吉兵，等.改进的变维滤波实现运动目标姿态的跟踪［J］.电光与控制，2012，19（3）:40 －43.

［4］吴勃，徐欢，乔相伟.状态切换UKF的飞行器姿态确定算法［J］.电机与控制学报，2012，16（6）:98－105.

［5］董欣远，王苏峰.QCDKF算法研究及其在小卫星姿态确定中的应用［J］.计算机工程与应用，2012，48（S2）:141－146.

［6］苏跃斌，辛长范，郭本亮，等.三维比例导引弹道的可视化仿真研究［J］.弹箭与制导学报，2010，30（4）:57－60.

［7］戴雪峰，金连文.基于OpenGL实现火箭弹道及卫星轨道三维可视化［J］.测控技术，2006，25（1）:17－19.