两种长基线模糊度解算方法在北斗三频应用中的比较*
2014-09-20黄令勇宁德阳吕志平
黄令勇 宁德阳 吕志平 崔 阳 吕 浩
1)信息工程大学地理空间信息学院,郑州 4500522)海洋测绘研究所,天津 300061
3)广空勘察设计院,广州 510000
两种长基线模糊度解算方法在北斗三频应用中的比较*
黄令勇1,2)宁德阳3)吕志平1)崔 阳1)吕 浩1)
1)信息工程大学地理空间信息学院,郑州 450052
2)海洋测绘研究所,天津 300061
3)广空勘察设计院,广州 510000
以三频模糊度解算TCAR算法为基础,利用北斗三频实测数据,对比分析了基于TCAR算法改进后的电离层改正法和无几何无电离层组合法解算北斗三频长基线模糊度的效果。结果表明,两种方法均能提高长基线模糊度固定的准确性,且经一定历元数据平滑后均可实现长基线模糊度的快速解算,从而有利于实现长距离北斗三频精密快速导航定位。
北斗;三频;长基线模糊度解算;电离层改正法;无几何无电离层组合法
随着北斗区域导航系统的运行,三频导航技术开始真正走向实用。北斗三频观测除了能够削弱大气传播误差、多路径效应等影响外,还可以实现模糊度的快速解算,缩短首次定位时间[1]。观测值域的三频模糊度解算方法最具代表性的算法是TCAR算法[2],其主要优势在于通过逐级取整固定三频组合观测值模糊度,避免了LAMBDA等方法的复杂搜索计算。TCAR方法能够快速实现短基线模糊度固定[3],但难以快速准确解算长基线模糊度[4]。文献[5]提出采用旋转矩阵变换的方法来解算长基线模糊度,但旋转矩阵的选取受观测值噪声影响,不同观测噪声所采用的旋转矩阵是不同的。为实现长基线模糊度固定,有学者对 TCAR 算法进行了改进[6-8],但主要是针对GPS系统的研究。由于北斗与GPS系统在频率、硬件设备等方面存在差异,电离层延迟改正法和无几何无电离层组合法在北斗三频模糊度解算中的应用仍值得进一步研究。为此,本文基于北斗三频实测数据,在分析TCAR算法的基础上,比较了以上两种方法固定长基线模糊度的效果,总结了两种算法的特点。
1 TCAR算法分析
TCAR(three carrier ambiguity resolution)算法的实质是利用两个特性较优的拍频组合,解算波长最长的模糊度,通过取整固定后作为已知值求解波长次长的模糊度,以最终确定初始模糊度值的“逐级求解”过程[3]。根据 TCAR 原理[9-10],假定北斗 B3频点伪距R3精度最高,北斗体制下TCAR解算模型为:为表述方便,式中均略去了双差符号;Nя、^Nя、λя、φя和eя(я∈[EWL,WL,B3])分别为模糊度浮点解和整周模糊度、波长、载波观测值、观测噪声,其中EWL、WL和B3分别表示超宽巷、宽巷和B3频点;I1为B1频点电离层延迟误差;αR3-EWL、αEWL-WL和 αWL-φ3分别表示相应组合观测值的电离层延迟系数。
由式(1)可知,不考虑多路径效应、接收机硬件延迟等误差,经双差处理后TCAR算法中的模糊度固定仅受噪声和电离层延迟的影响。以表1中的北斗拍频组合为例,假定北斗伪距噪声为0.3 m,载波噪声为0.01周,双差后电离层延迟残差为2×10-6。在上述观测条件下,观测误差大小仅与基线距离有关。由文献[4]依据概率统计法给出的模糊度固定成功率计算公式,根据式(1)进行误差分析,计算TCAR各步骤模糊度固定成功率随基线长度的变化情况,如图1所示。
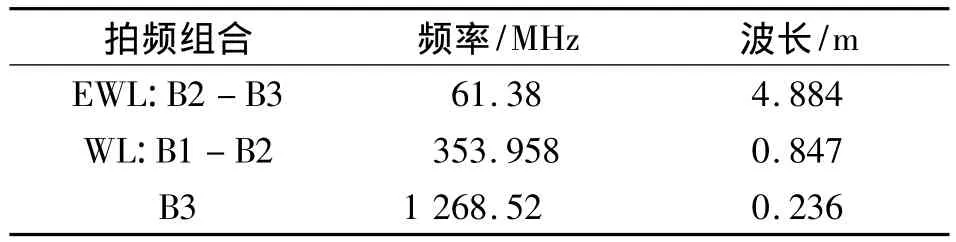
表1 TCAR拍频组合Tab.1 Beat frequency of TCAR
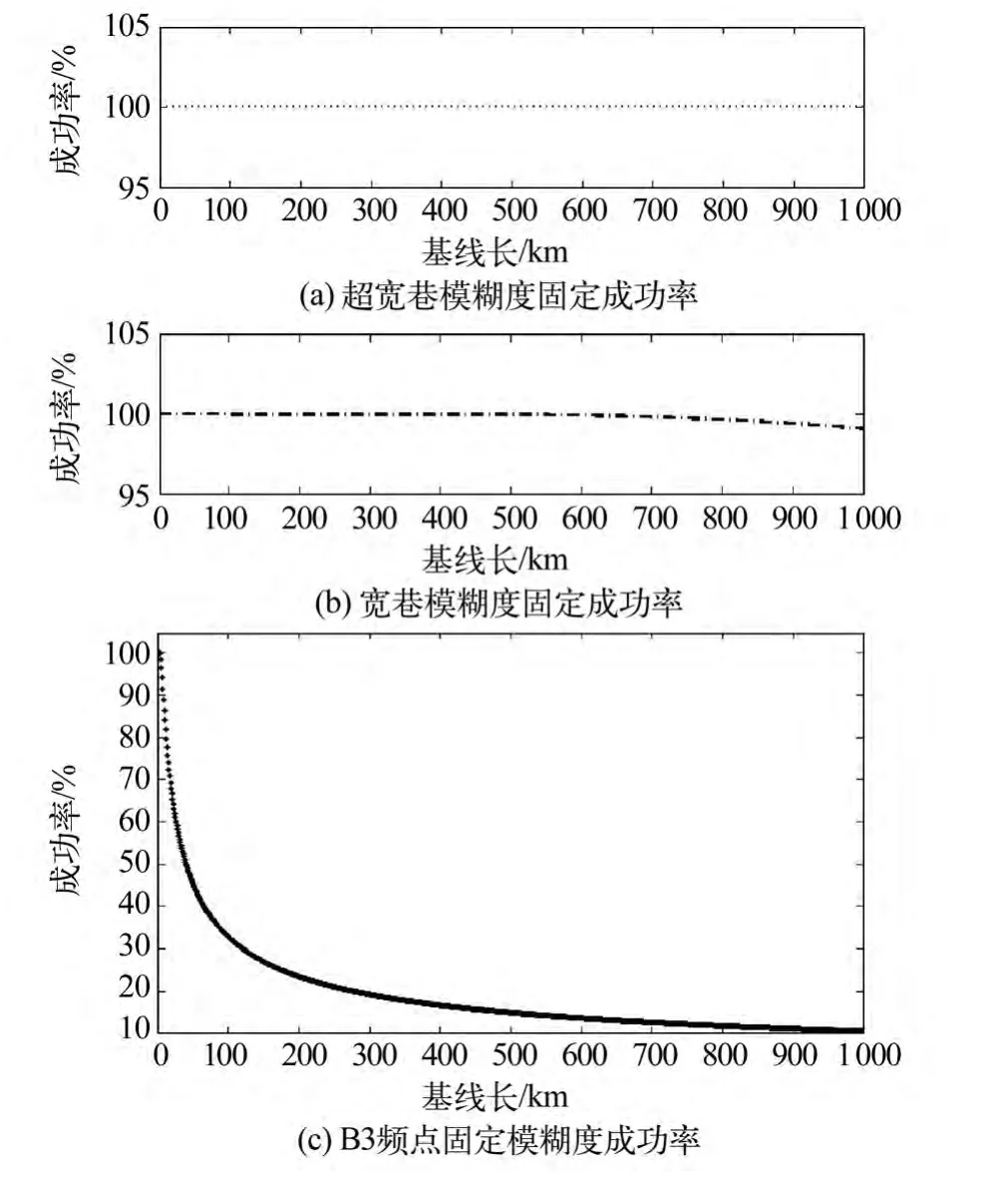
图1 模糊度固定成功率Fig.1 The successful rate of ambiguity resolution
由图1可知,当基线长达数百或上千km时,超宽巷、宽巷模糊度固定仍具有很高的成功率,这是因为虽然相比超宽巷组合,宽巷组合波长变短,但超宽巷模糊度固定以后,站星距离相比伪距精度有了很大精化,且超宽巷组合与宽巷组合观测值差分后的电离层延迟误差相对宽巷组合波长仍然较小,故宽巷组合仍有很高的固定成功率。但B3频点模糊度固定成功率却随着距离的增加而迅速下降,其主要是由于原始B3频点波长较短,在观测噪声一定时,随着基线增长电离层延迟残差影响逐渐增大,以致B3频点模糊度固定受到的误差影响变大,使其固定成功率降低。由此可知,电离层延迟残差是影响TCAR长基线模糊度固定的主要因素。
2 电离层延迟改正法
根据图1可知,长基线超宽巷、宽巷模糊度能以很高的成功率准确固定,为此可利用模糊度固定后的超宽巷和宽巷观测方程计算电离层延迟量,然后改正原始观测方程的电离层延迟,从而提高原始模糊度固定成功率。超宽巷和宽巷模糊度固定后的载波观测方程可表示为:

式中,ρ和T分别为站星几何距离与对流层延迟量。由式(2)计算电离层延迟I1:

将式(3)代入式(2)求解原始频点的电离层延迟误差,进而由式(1)中第3式固定原始模糊度。此时原始频点模糊度标准差为:

由式(4)可知,电离层改正后消除了电离层延迟对原始频点模糊度固定的影响,使得模糊度固定更准确,但电离层延迟改正会放大观测噪声,进而影响模糊度固定效果。由于观测噪声为随机量,可采用数据平滑进行消噪处理,具体方法见文献[5]。
3 无几何无电离层组合法
由于无几何无电离层组合仅受观测噪声影响,消除了电离层延迟的影响,故可通过无几何无电离层组合观测值模糊度固定来代替TCAR算法中受电离层延迟影响较大的原始模糊度解算。由TCAR算法可知,长基线超宽巷模糊度易于固定,为此基于多频组合理论,在构造无几何无电离层组合时,选择两个超宽巷和一个窄巷组合线性组合得到无几何无电离层组合[8]:
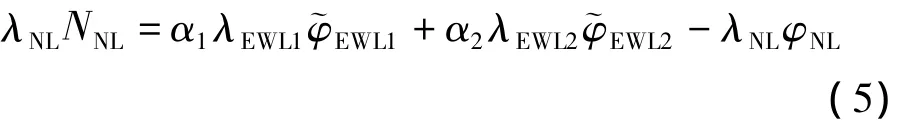

记(i,j,k)和(m1,n1,l1)、(m2,n2,l2)分别为窄巷和两个超宽巷的组合系数,则式(5)中窄巷模糊度中误差为:

假定北斗载波噪声为0.01 m,选取一组较优的北斗三频组合(表2),根据式(5)构造出相应的无几何无电离层组合,并对无几何无电离层组合模糊度的标准差进行分析(表3)。

表2 较优的北斗三频组合Tab.2 Beidou optimized combination

表3 北斗无几何无电离层组合观测值Tab.3 Beidou free-geometry and free-ionospheric combination
表3中以周为单位的北斗无几何无电离层组合模糊度标准差大致相同,均在10周左右,即噪声会导致模糊度浮点波动范围较大,仍难以实现模糊度的直接取整固定,但由于此时模糊度固定仅受观测噪声影响,故同样可以通过数据平滑削弱噪声影响,进而实现模糊度的快速固定。北斗载波实际噪声要小于0.01 m,故该组合方法的模糊度数据平滑固定更容易。
4 实验分析
利用北京站和三亚站2011-09-17 00:00共600历元、采样间隔为1 s的G1、G4卫星数据,分别对表1中的拍频组合采用电离层改正法,对表3中的无几何无电离层组合采用无几何无电离层组合法进行实验分析。
图2(a)所示超宽巷、宽巷模糊度浮点的波动范围均非常小,每个历元均可直接通过取整固定得到相同的整周模糊度值。但分析可知,长基线时两端电离层延迟相关性弱,双差后电离层延迟残差仍然较大,影响了模糊度固定成功率。由图2(b)可知,经电离层延迟改正后可消除电离层延迟残差对B3模糊度解算的影响,提高模糊度解算的准确性,但电离层改正后的B3频点模糊度浮点解比改正前波动范围大(图2(b)),其原因可由式(4)分析得知,电离层延迟改正放大了观测噪声,进而使相邻历元间模糊度浮点解相差较大。

图2 电离层延迟改正法解算长基线模糊度Fig.2 The method of ionospheric correction for long baseline ambiguity resolution
为削弱噪声对B3模糊度解算的影响,对观测数据进行平滑消噪,具体方法为:对第200~400历元间的每一历元数据向前向后各取199个历元进行滤波处理,然后再解算B3模糊度,其浮点解如图2(c)所示。此时B3模糊度浮点解上下波动明显变小,说明数据平滑消噪作用显著。虽然B3浮点解在-235 023 8.5附近,模糊度值确定还需要进一步验证,但基本已无计算开销。由此可知,电离层延迟改正法仅需数分钟的数据平滑消噪便可实现长基线模糊度的快速解算。

图3 无几何无电离层组合法解算长基线模糊度Fig.3 The method of geometry-free and ionosphere-free combination for long baseline ambiguity resolution
图3(a)中,两个超宽巷模糊度浮点解波动范围均较小,每一历元取整得到的模糊度是一致的,这再次证明了长基线超宽巷组合模糊度解算的优势。图3(b)所示的无几何无电离层组合的模糊度浮点解波动范围均较大,上下波动约在10周左右,说明观测噪声对模糊度解算的影响非常显著。经数据平滑消噪后,模糊度浮点解波动范围大大降低(图3(c)),此时每个历元取整后的模糊度整数解是相同的。由此可知,数据平滑消噪后,无几何无电离层组合同样可以实现长基线模糊度的快速解算。
需要说明的是,图3(c)中无几何无电离层组合[#1#2#5]解算得到的B3频点模糊度值与图2(c)中得到的B3模糊度浮点解大约相差15周左右,造成解不一致的原因在于:本实验仅关心模糊度解算问题,未对实测数据中的多路径误差、接收机硬件延迟等误差进行预处理,而短时间内的数据平滑处理难以削弱这两种误差,而由式(2)和(5)可知,这两种系统误差在两种算法中的系数大小是不一致的,当不同大小的误差被两种算法中的模糊度吸收后,便导致两种算法解算的B3模糊度不一致。但这并不影响两种方法在快速解算长基线模糊度中的优势。
5 结语
根据分析可知,TCAR算法很容易实现长基线超宽巷、宽巷模糊度的快速解算,而窄巷或原始频点模糊度的解算主要受到电离层延迟残差的影响,导致模糊度固定成功率较低。电离层延迟改正法可以消除电离层延迟影响,无几何无电离层组合可以消除几何误差和电离层延迟误差,使模糊度解算仅受观测噪声影响。虽然电离层延迟改正以及无几何无电离层组合会放大观测噪声,但经数据平滑消噪后可实现模糊度的快速解算。
1 杨元喜.北斗卫星导航系统的进展、贡献与挑战[J].测绘学报,2010,39(1):1 -6.(Yang Yuanxi.Progress,contribution and challenges of Compass/Beidou satellite navigation system[J].Acta Geodaetica et Cartographica Sinica,2010,39(1):1-6)
2 Birnbachs V.Analysis of three carrier ambiguity resolution(TCAR)technique for precise relative positioning in GNSS-2[C].ION GPS-98,Toulouse,1998.
3 范建军,王飞雪.一种短基线GNSS的三频模糊度解算(TCAR)方法[J].测绘学报,2007,36(1):43 -49.(Fan Jianjun,Wang Feixue.A method for GNSS three frequency ambiguity resolution based on short baselines[J].Acta Geodaetica ed Cartographcia Sinica,2007,36(1):43 -49)
4 黄令勇.GNSS多频数据处理理论与方法研究[D].郑州:信息工程大学,2012.(Huang Lingyong.Research on the algorithms and theory of GNSS multi-frequency data processing[D].Zhengzhou:Information Engineering University,2012)
5 黄令勇.基于矩阵变换算法的长基线多频模糊度快速解算[J].大地测量与地球动力学,2012(5):133 -136.(Huang Lingyong.A new method based on matrix transformation algorithm for long baseline multi-frequency rapid ambiguity resolution[J].Journal of Geodesy and Geodynamics,2012(5):133-136)
6 伍岳.TCAR/MCAR方法在不同距离基线模糊度求解中的应用[J].武汉大学学报:信息科学版,2007,32(2):172-175.(Wu Yue.Application of TCAR/MCAR method in different baseline ambiguity resolution[J].Geomatics and Information Science of Wuhan University,2007,32(2):172-175)
7 Li Bofeng,Feng Yanming,Shen Yunzhong.Three carrier ambiguity resolution:distance-independent performance demonstrated using semi-generated triple frequency GPS signals[J].GPS Solution,2010,14:177 -184.
8 李博峰,沈云中,周泽波.中长基线三频GNSS模糊度的快速算法[J].测绘学报,2009,38(4):296 -300.(Li Bofeng,Shen Yunzhong,Zhou Zebo.A new method for medium and long range three frequency GNSS rapid ambiguity resolution[J].Acta Geodaetica et Cartographica Sinica,2009,38(4):296-300)
9 Feng Yanming.GNSS three carrier ambiguity resolution using ionosphere-reduced virtual signals[J].Journal of Geodesy,2008,82:847 -862.
10 Feng Yanming,Rizos C.Network-based geometry - free three carrier ambiguity resolution and phase bias calibration[J].GPS Solution,2009,13:43 -56.
COMPARATIVE STUDY ON TWO LONG-BASELINE AMBIGUITY RESOLUTION METHODS IN APPLICATION OF BEIDOU/COMPASS TRIPLE-FREQUENCY
Huang Lingyong1,2),Ning Deyang3),Lü Zhiping1),Cui Yang1)and Lü Hao1)
1)Institute of Geospatial Information,Information Engineering University,Zhengzhou 450052
2)Institute of Hydrographic Surveying and Charting,Tianjin 300061
3)Guangkong Institute of Survey and Design,Guangzhou510000
On the bisis of the three carrier ambiguity resolution(TCAR)algorithm,the two improved methods,ionospheric delay correction method and the method of geometry-free and ionosphere-free combination,were compared and analyzed with the Beidou/Compass triple-frequency surveying data.The experiment results show that both methods can improve the accuracy of long-baseline ambiguity resolution,and a rapid long-baseline ambiguity resolution after data smoothing with some epochs can be realized.The two methods can be useful for achieving the longbaseline precise rapid navigation and position with Beidou/Compass triple-frequency.
Beidou/Compass;triple-frequency;ambiguity resolution for long-baseline;ionospheric delay correction method;geometry-free and ionosphere-free combination method
P228
A
1671-5942(2014)05-0101-05
2013-06-24
国家自然科学基金项目(41274015,41274045,41374042);国家863计划项目(2013AA122501)。
黄令勇,男,1987年生,博士生。主要从事测量数据处理理论与方法研究。E-mail:hlylj87@126.com。
