PPP星间单差整周模糊度的固定方法与结果分析*

潘 林 蔡昌盛 朱建军

(中南大学地球科学与信息物理学院，长沙 410083)

PPP星间单差整周模糊度的固定方法与结果分析*

潘 林 蔡昌盛 朱建军

(中南大学地球科学与信息物理学院，长沙 410083)

为消除载波相位观测值中存在的小数偏差项，将消电离层模糊度分解为宽巷模糊度与窄巷模糊度，通过星间单差消除接收机端的宽巷模糊度与窄巷模糊度小数偏差，并利用卫星端宽巷模糊度小数偏差恢复宽巷模糊度的整数特性，而卫星端的窄巷模糊度小数偏差则包含在CNES提供的精密卫星钟差数据中，应用其钟差数据也可以恢复窄巷模糊度的整数特性。利用IGS站观测数据进行分析表明，模糊度固定成整数后，星间单差精密单点定位固定解与非差精密单点定位浮点解相比，定位精度有显著改善，三维定位精度的最大改善率达63.8%。

精密单点定位;整周模糊度;小数偏差;宽巷模糊度;窄巷模糊度

利用IGS分析中心提供的精密轨道和精密钟差数据进行精密单点定位(PPP)，可以得到cm级甚至mm级的定位精度［1］。但传统的PPP中，非差载波相位观测值中存在源自于接收机和卫星的小数偏差项(FCB，fractional cycle biases)，而且这些小数偏差与非差整周模糊度难以分离［2］，破坏了模糊度的整数特性，致使模糊度只能当作浮点数处理，限制了精密单点定位精度的进一步提高。针对这一问题，目前主要有两种方法:借助全球或者广域参考网站的数据，将小数偏差项估计出来［2－6］;从钟差估计的角度，利用卫星钟差和接收机钟差分别吸收卫星端和接收机端的小数偏差项［7－8］。目前用第一种方法得到的小数偏差数据还没有公布。而第二种方法中，通常采用非差观测值进行解算，使用吸收了卫星端小数偏差的精密卫星钟差数据，只进行了卫星端小数偏差改正，并认为在解算过程中，接收机钟差会吸收接收机端的小数偏差。实际上，接收机钟差不可能完全吸收接收机端的小数偏差，因而模糊度固定必然会受到接收机端小数偏差项的影响。

本文在将消电离层模糊度分解成宽巷模糊度和窄巷模糊度的基础上，通过星间单差操作来消除接收机端的宽巷模糊度与窄巷模糊度小数偏差，然后根据CNES提供的卫星端宽巷模糊度小数偏差改正观测值，以恢复宽巷模糊度的整数特性。而CNES提供的精密卫星钟差数据在生成的过程中吸收了卫星端的窄巷模糊度小数偏差［9］，因此，应用其钟差数据也可以恢复窄巷模糊度的整数特性。利用IGS站提供的数据进行分析表明，在模糊度固定成整数后，星间单差PPP固定解与非差PPP浮点解相比定位精度有显著提高。

1 固定整周模糊度的PPP实施方法

1.1 PPP误差源与改正方法

1)卫星轨道和钟的误差:使用CNES提供的精密轨道和精密卫星钟差数据，精密轨道的精度优于5 cm，精密卫星钟差的精度优于0.12 ns，满足PPP中固定窄巷模糊度的精度要求［9］。

2)电离层延迟:采用消电离层组合消除一阶电离层误差的影响，而高阶电离层误差模型因为复杂且影响较小，在太阳活动不剧烈时可以忽略不计。

3)对流层延迟:对流层延迟值随高度角在2.4～25 m 之间变化［10］。干分量通过 Hopfield 模型［11］进行改正，湿分量作为未知参数进行估计，使用的投影函数为 Niell［12］。

4)DCB(differential code biases):由于CNES所提供的精密轨道和精密卫星钟差数据是相对于P码观测值的，因此如果用户观测文件中使用的是C/A码观测值，就必须进行DCB改正。DCB的影响可达1.2 m，约1.4个宽巷模糊度波长，如果不进行DCB改正，可能导致宽巷模糊度固定不准确。IGS分析中心CODE按月提供DCB改正数据［13］。

5)天线相位中心偏差:天线相位中心偏差可达dm级［14］，因此在PPP中必须进行改正。IGS所提供的ATX文件给出了卫星天线相位中心改正与接收机天线相位中心改正的数据。

6)天线相位缠绕:天线相位缠绕对PPP的影响十分显著，能达到半个波长，如果忽略将使得定位精度只能达到dm级，因此在PPP中必须进行天线相位缠绕改正［15］。

7)固体潮、大洋负荷与大气负荷:固体潮可以引起径向30 cm、水平方向5 cm的定位误差，因此必须进行改正［16］;而大洋负荷和大气负荷引起的误差很小［16－17］，在处理过程中可以忽略。

1.2 宽巷模糊度固定

在GPS卫星定位中，常用的观测值有测码伪距和载波相位观测值。对于双频接收机，测码伪距和载波相位观测值可以表示为:

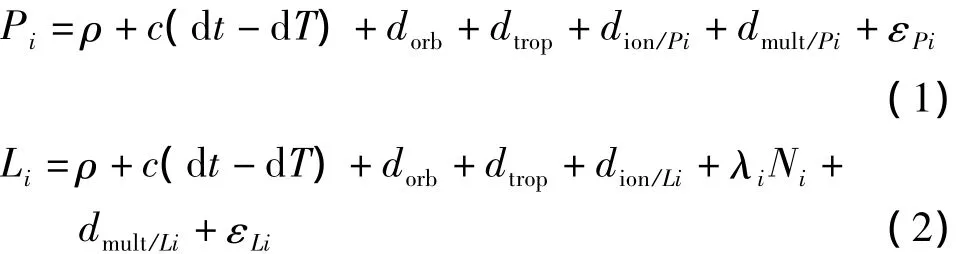
式中，i(i=1，2)表示GPS卫星的两个频率，P是伪距观测值，L是载波相位观测值，ρ是卫星到测站之间的几何距离，c是光速，dt是接收机钟差，dT是卫星钟差，dorb是卫星轨道误差，dtrop是对流层延迟，dion是电离层延迟，λ是载波相位观测值的波长，N是载波相位观测值上的整周模糊度，dmult是多路径误差，ε是观测噪声。

为了消除接收机端的小数偏差，需要进行星间单差操作，公式为:

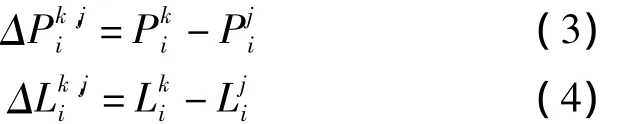
式中，k与j分别代表一颗GPS卫星，其中j代表参考卫星，并且满足k≠j。

宽巷模糊度通过Melbourne-Wubbena组合观测值［18－19］计算得到，计算公式为:

在固定宽巷模糊度之前，还需要进行卫星端宽巷模糊度小数偏差改正，来恢复宽巷模糊度的整数特性。CNES中心提供每日更新的卫星端宽巷模糊度小数偏差改正［9］，图1显示的是2012-11-30的32颗GPS卫星的卫星端宽巷模糊度小数偏差改正值。从图中可知，个别卫星的宽巷模糊度小数偏差改正甚至达到1周，如果不进行改正，可能导致宽巷模糊度固定不准确。

图1 2012-11-30卫星端宽巷模糊度小数偏差改正Fig.1 Satellite FCB corrections of wide-lane ambiguities on November 30，2012

宽巷模糊度波长达0.86 m，可以直接通过取整运算来固定，但由于观测噪声较大，可能导致个别历元的宽巷模糊度固定不准确，所以需要对其进行平滑来提高模糊度固定的准确率和可靠性。在进行平滑操作之前，还需进行周跳探测，若有周跳发生，必须从周跳发生的历元重新进行平滑计算。本文使用TurboEdit方法［20］进行周跳探测。

1.3 窄巷模糊度固定

为了消除一阶电离层误差的影响，精密单点定位中通常使用消电离层组合观测值，公式为:

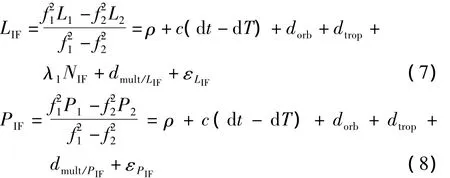
式中，NIF是消电离层模糊度，它可以分解成宽巷模糊度NWL与窄巷模糊度N1，其星间单差形式为:

本文使用Kalman滤波进行解算，在宽巷模糊度固定成整数后，窄巷模糊度作为一个未知参数在Kalman滤波中进行估计。由于模糊度固定需要30～60 min［9，21］，所以对观测时间少于 30 min 的卫星进行剔除。窄巷模糊度的固定方法同样是直接取整。由于浮点模糊度在收敛前误差较大，我们没有对每个历元直接固定，而是取观测时段最后一个历元的窄巷模糊度进行固定，以此来作为这颗卫星所有历元的窄巷模糊度固定值。如果有周跳发生，则分段进行上述操作，因此该方法仅适用于精密单点定位事后处理。

由于窄巷模糊度的波长只有0.19 m，个别卫星的窄巷模糊度可能固定不准确。当窄巷模糊度固定不准确时，相当于引入粗差到观测值中，所以必须进行质量控制来识别窄巷模糊度固定错误的卫星。质量控制的公式为:

式中，H是系数阵，P－是预报的参数方差协方差阵，R是观测值方差协方差阵，σP是测码伪距改正值的中误差，σL是载波相位改正值的中误差，σPL是测码伪距改正值与载波相位改正值的协方差，vP是测码伪距观测值与预报值之差，vL是载波相位观测值与预报值之差，n是进行质量控制所取的倍数。n是经验值，经验证，n取8时效果较好。

当某颗卫星不满足式(12)时，认为这颗卫星的窄巷模糊度固定不准确。这时，对这颗卫星的窄巷模糊度进行±2周内的搜索，找到vP与vL最小的窄巷模糊度。如果最小的 vP与 vL仍然不满足式(12)，则剔除这颗卫星。

当窄巷模糊度固定成整数后，需要再一次进行Kalman滤波解算，此时宽巷模糊度和窄巷模糊度均为已知值，待估参数只有三维位置坐标和天顶对流层湿分量延迟。

现取2012-11-30 HERT站02:00～05:00的观测数据对质量控制的重要性进行说明。图2是进行质量控制与不进行质量控制两种情况下星间单差PPP固定解的三维定位误差对比。从图2可知，若不进行质量控制，定位结果将出现严重的发散现象，说明个别卫星的窄巷模糊度固定不准确;而进行质量控制时，无发散情况出现，定位结果收敛到cm级。

2 结果与分析

选取 2012-11-30 HERT、LAMA、MATE、SOFI、WTZR、ZIM2 6个 IGS站02:00～05:00、05:00～08:00、08:00～11:00(GPS时)的观测数据进行分析，数据采样间隔30 s，截止高度角15°。

图3为HERT站02:00～05:00观测数据非差浮点解与星间单差固定解的定位误差。从图中可知，模糊度固定成整数后，东方向、北方向、高程方向的定位精度均有显著提高。和非差浮点解相比，星间单差固定解具有更好的可靠性和稳定性。

图2 有无质量控制的星间单差PPP固定解三维定位误差对比Fig.2 Comparison of 3-D position errors for PPP fixed resolution with and without quality control

图3 HERT站02:00～05:00观测数据非差浮点解与星间单差固定解定位误差对比Fig.3 Comparison of position errors with zero-difference PPP float resolution and with between-satellitedifference PPP fixed resolution using observation data from 2 to 5 at HERT

图4为6个IGS站02:00～05:00观测数据非差浮点解与星间单差固定解3个方向定位误差的RMS统计值，统计时间是观测时段最后20 min。从图中可知，除SOFI站的高程方向与WTZR站的北方向之外，星间单差固定解的定位精度均有显著提高。为了更加清楚地反映星间单差固定解相比非差浮点解定位精度的改善情况，表1给出了6个IGS站3个时段观测数据的非差浮点解与星间单差固定解三维定位误差的RMS统计值。从表中可知，模糊度固定之前，有5组观测数据的三维定位误差达到1 dm以上，而模糊度固定之后，三维定位误差大幅降低，均在cm级。和非差浮点解相比，星间单差固定解三维定位精度的最大改善率达到63.8%。

图4 02:00～05:00观测数据非差浮点解与星间单差固定解定位误差的RMS比较Fig．4 RMS comparison of position errors with zero-difference PPP float resolution and with between-satellitedifference PPP fixed resolution from 2 to 5

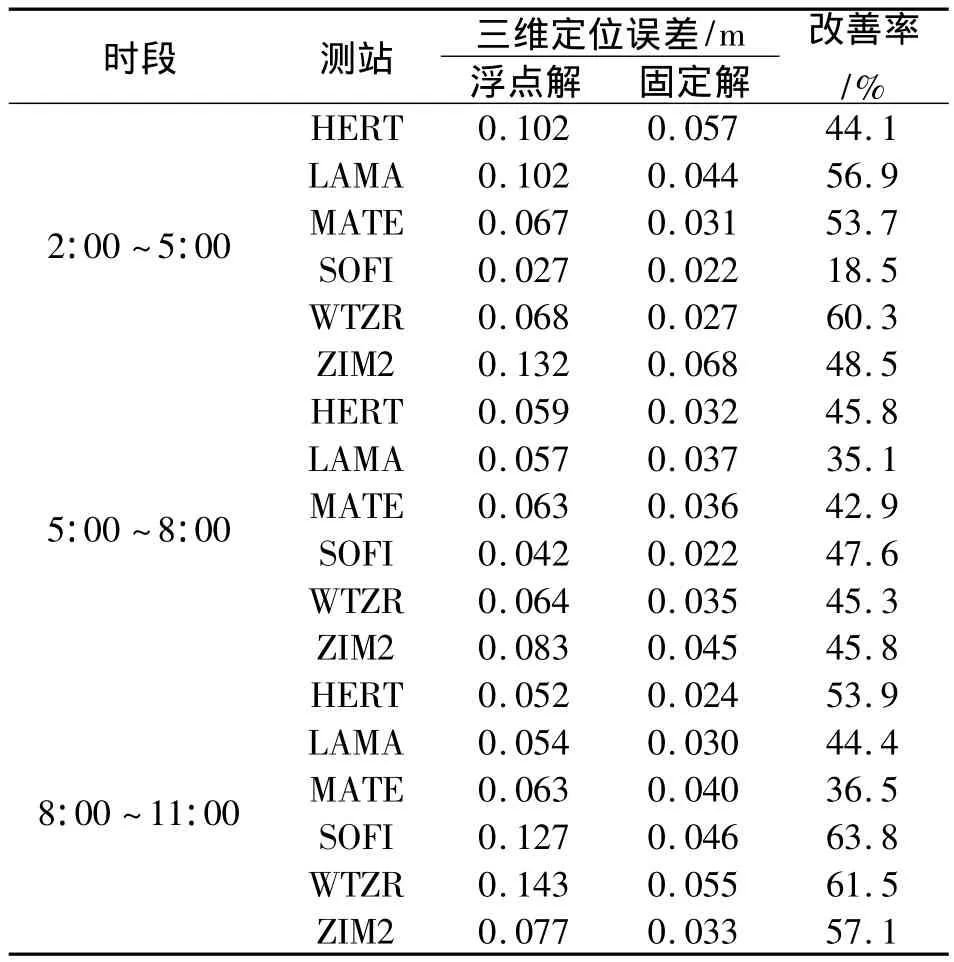
表1 非差浮点解与星间单差固定解三维定位误差RMS比较Tab.1 RMS comparison of 3-D position errors with zerodifference PPP float resolution and with betweensatellite-difference PPP fixed resolution

3 结论

本文将消电离层模糊度分解成宽巷模糊度和窄巷模糊度，通过星间单差操作来移除接收机端的宽巷模糊度与窄巷模糊度小数偏差，然后利用IGS分析中心CNES提供的卫星端宽巷模糊度小数偏差值恢复宽巷模糊度的整数特性，而CNES提供的精密卫星钟差数据在生成过程中吸收了卫星端的窄巷模糊度小数偏差，因此，应用其钟差数据也可以恢复窄巷模糊度的整数特性。

利用6个IGS站提供的观测数据进行分析，结果表明，模糊度固定成整数后，星间单差固定解和非差浮点解相比，定位精度有显著改善，三维定位精度的最大改善率达到63.8%。

1 Zumberge J F.Precise point positioning for the efficient and robust analysis of GPS data from large networks［J］.Journal of Geophysical Research，1997，102(B3):5 005 －5 017.

2 Ge M.Resolution of GPS carrier-phase ambiguities in precise point positioning(PPP)with daily observations［J］.J Geod，2008，82(7):389 －399.

3 Geng J.Ambiguity resolution in precise point positioning with hourly data［J］.GPS Solution，2009，13(4):263 －270.

4 Geng J.Kinematic precise point positioning at remote marine platforms［J］.GPS Solution，2010，14(4):343 － 350.

5 Zhang X H，Li P，Guo F.Ambiguity resolution in precise point positioning with hourly data for global single receiver［J］.Advances in Space Research，2012，51(1):153 －161.

6 Li X X，Zhang X H.Improving the estimation of uncalibrated fractional phase offsets for PPP ambiguity resolution［J］.The Journal of Navigation，2012，65:513 －529.

7 Laurichesse D.Integer ambiguity resolution on undifferenced GPS phase measure-ments and its application to PPP and satellite precise orbit determination［J］.Navig J Inst Navig，2009，56(2):135 －149.

8 Collin P.Isolating and estimating undifferenced GPS integer ambiguities［C］.ION National Technical Meeting，San Diego，USA，2008.

9 Laurichesse D.The CNES real-time PPP with undifferenced integer ambiguity resolution demonstrator［C］.24th International Technical Meeting of the Satellite Division of the Institute of Navigation(ION GNSS 2011)，Portland，2011.

10 Kaplan E D，Hegarty C J.Understanding GPS principles and applications［M］.Artech House，2006.

11 Wielgosz P.Results of the application of tropospheric corrections from different troposphere models for precise GPS rapid static positioning［J］.Acta Geophysica，2012，60(4):1 236－1 257.

12 Niell A E.Global mapping functions for the atmosphere delay at radio wavelengths［J］.Journal of Geophysical Research，1996，101:3 227 －3 246.

13 Dach R.Bernese GPS software version 5.0 user manual［Z］.2007.

14 Abdel-salam M.Precise point positioning using un-differenced code and carrier phase observations［D］.University of Calgary，2005.

15 Kouba J，Héroux P.Precise point positioning using IGS orbit products［J］.GPS Solution，2000，5(2):12 －28.

16 Kouba J.A guide to using International GNSS Service(IGS)products［EB/OL］.http://igscb.jpl.nasa.gov/igscb/resource/pubs/UsingIGSProductsVer21.pdf，2009.

17 Urquhart L.Atmospheric pressure loading and its effects on precise point positioning［C］.22nd International Technical Meeting of the Satellite Division of the Institute of Navigation(ION GNSS 2009)，2001.

18 Melbourne W G.The case for ranging in GPS-based geodetic systems［C］.The First International Symposium on Precise Positioning with the Global Positioning System，Rockville，Maryland，USA，1985.

19 Wubbean G.Software developments for geodetic positioning with GPS using TI 4100 code and carrier measurements［C］.The First International Symposium on Precise Positioning with the Global Positioning System，Rockville，Maryland，USA，1985.

20 Geoffrey B.An automatic editing algorithm for GPS data［J］.Geophysical Research Letters，1990，17(3):199 －202.

21 Geng J.Towards PPP-RTK:Ambiguity resolution in realtime precise point positioning［J］.Advances in Space Research，2011，47:1 664 －1 673.

THE METHODS AND RESULTS OF PRECISE POINT POSITIONING WITH BETWEEN-SATELLITE-DIFFERENCE INTEGER AMBIGUITY FIXING

Pan Lin，Cai Changsheng and Zhu Jianjun
(School of Geosciences and Info-Physics，Central South University，Changsha 410083)

In the traditional precise point positioning(PPP)，the integer ambiguity can only be estimated as float value，which restricts the further enhance of PPP accuracy for the existence of fractional cycle biases(FCB)in the carrier phase observations from the receiver and satellite ends.In the study，the ionosphere-free ambiguity is decomposed into wide-lane(WL)and narrow-lane(NL)ambiguities.The between-satellite-difference(BSD)operation can remove the FCB included in WL and NL ambiguities at the receiver end.The satellite-based FCB contained in the WL ambiguity provided by the international GNSS service(IGS)analysis center CNES can be used to recover the integer nature of the WL ambiguity.Due to the precise satellite clock corrections provided by CNES assimilate the satellite-based FCB of the NL ambiguity，the integer nature of NL ambiguity can also be recovered after applying the precise clock corrections.The analysis results based on the IGS observation data indicate that the positioning accuracy of BSD PPP fixed resolution is significantly better than the zero-difference(ZD)PPP float resolution.The improvement rate of 3-dimensional positioning accuracy reaches 63.8%.

precise point positioning(PPP);integer ambiguity resolution;fractional cycle biases;wide-lane ambiguity;narrow-lane ambiguity

P228.4

A

1671-5942(2014)05-0090-04

2013-11-01

国家自然科学基金项目(41004011)。

潘林，男，1989年生，硕士研究生，主要研究方向为GNSS导航和精密单点定位。E－mail:panlin15116333665@163.com。