基于顶点排序的三维模型数字水印算法
2014-09-19翟浩,杨有,万辉
翟 浩,杨 有,万 辉
(1.重庆师范大学计算机信息与科学学院,重庆 401331;2.重庆师范大学科研处,重庆 401331)
基于顶点排序的三维模型数字水印算法
翟 浩1,杨 有1,万 辉2
(1.重庆师范大学计算机信息与科学学院,重庆 401331;2.重庆师范大学科研处,重庆 401331)
提出一种基于顶点排序的三维模型多重数字水印算法.算法的主要思想是首先将三维模型进行定位、定向以及定型,将此状态作为三维模型的初始状态;然后利用LSB的方法将水印信息多重循环嵌入到该三维模型中,以提高水印信息的鲁棒性.实验结果表明,该算法针对平移、旋转、全比例缩放和细分等攻击具有很高的鲁棒性,针对单比例缩放、剪切和简化攻击,鲁棒性有待进一步提高.该算法可以有效保护三维模型的版权.
数字水印;三维模型;顶点排序;多重水印
1 本文算法
本文算法是将文字信息作为水印信息,而将三维模型作为嵌入载体.嵌入过程是首先将文字信息转换成GB2312码,得到二进制信息,对二进制信息采用异或加密.然后将三维模型的中心坐标求出来,将三维模型的中心坐标移至坐标原点,以应对平移变换,接着将三维模型的方向特征向量求出来,使该向量与Z轴一致,以应对旋转变换.接着将三维模型的中心坐标到三维模型各顶点的平均距离求出来,以便将来对嵌入水印的模型进行缩放修改,以使模型恢复到嵌入水印之前的状态.最后对三维模型的顶点根据原点到三维模型各顶点的距离进行从小到大的排序,然后将已经加密的二进制信息多次循环嵌入到已排序的顶点上,嵌入水印信息之前加上0000 0000 0000 0000作为水印起始标记,水印信息之后加上0000 0000 0000 0000作为水印结束标记,并利用LSB的方法多次循环嵌入到该三维模型中.水印提取过程是首先将三维模型的中心坐标求出来,通过平移变换,将三维模型的中心移至三维坐标原点.接着求出三维模型的方向特征向量,根据三角形的三角变换,进行沿X轴、Y轴的对应旋转后,使该向量与Z轴一致,就达到了旋转不变性的要求.然后求得三维模型的中心点到模型各顶点的平均距离,将此距离与嵌入水印前的平均距离相除,以求得缩放倍数,对带有水印信息的三维模型按比例缩放,以达到缩放不变性.最后对三维模型按照中心点到模型各顶点的距离按从小到大的顺序进行排序,按照此顺序依次从带有水印信息的各顶点提取出多组水印信息,分别计算相关值,并取最大的相关值作为实验结果.水印检测过程主要是根据相关值公式求得提取出来的二进制信息和嵌入的二进制信息的相关性,并通过阈值来判定提取出来的二进制信息是否能证明该模型的所有权.
1.1 水印嵌入过程
首先,根据GB2312码将水印信息(这里取“翟浩”)转换成二进制数据,在对此二进制数据与10进行异或,从而得到加密的二进制数据.然后的工作就是获取三维模型各顶点的横坐标、纵坐标以及竖坐标的坐标信息.首先需要确定三维模型的中心坐标:

为了最大限度地恢复嵌入水印之前三维模型的状态,需要对所有顶点进行计算,并取其所有顶点坐标的平均值,将此坐标移回到坐标原点,然后去求三维模型的方向特征向量:

将该三维模型沿Z轴旋转α度,在沿Y轴旋转β度,就使该三维模型的方向特征向量与Z轴
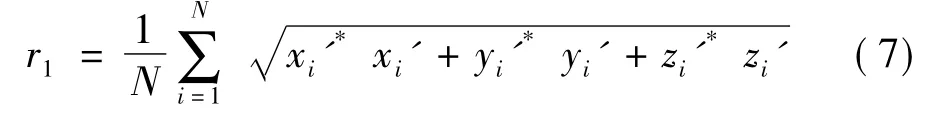
最后对三维模型的所有顶点按中心点到模型各顶点的距离从小到大进行排序,对于距离相等的,则按X轴坐标进行从小到大排序;对于距离大小和X轴坐标都相等的,则对Y轴坐标进行从小到大排序;对于距离大小、X轴坐标、Y轴坐标都相等的,则按Z轴坐标进行从小到大的排序.最终得到确定三维顶点的一维排序.最后将二进制水印信息前面加上0000 0000 0000 0000作为水印起始标记,尾部加上0000 0000 0000 0000作为水印结束标记,利用LSB的方法多重循环嵌入到已排序的顶点上.
方向一致.接着求原点到3D模型各顶点的平均距离r1,为使将来提取水印信息时提供参考依据,以应对缩放变换.

图1 旋转参考图
1.2 水印提取过程
首先,需要做的是将三维模型恢复到嵌入水印信息前的状态,这就涉及到对现有的三维模型进行重定位.先求出含水印三维模型的中心坐标:
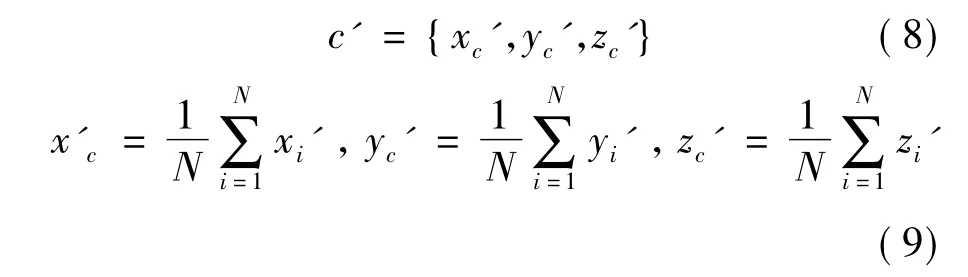
将该三维模型沿逆方向分别移动Xc'、Yc'、Zc',使该三维模型的中心坐标移至嵌入水印之前的位置,以抵抗平移攻击.求出三维模型的方向特征向量:
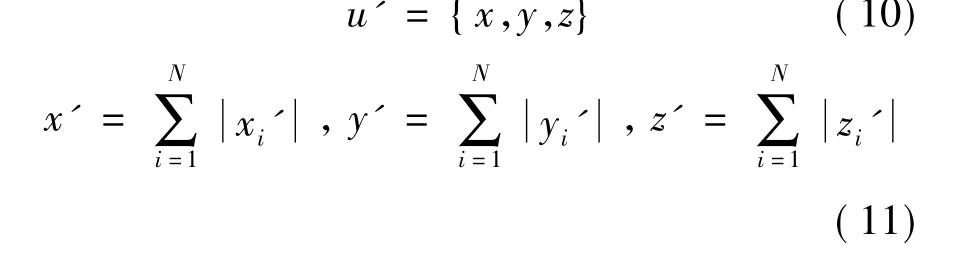

从而求得三维模型的方向特征向量,然后根据图1所示求得旋转角度α,β.

将该三维模型沿Z轴旋转α度,再沿Y轴旋转β度,就使该三维模型的方向特征向量与Z轴方向一致;接着求该原点到三维模型各顶点的平均距离:

根据原始模型的平均距离r1和嵌入水印后三维模型的平均距离r2,还需要求出缩放倍数s:

s就是所谓的缩放倍数,对水印模型进行缩放s倍,使水印模型尽可能恢复到嵌入水印之前的状态.最后对三维模型的所有顶点按原点到模型各顶点的距离从小到大进行排序;对于距离相等的,则按X轴坐标进行从小到大排序;对于距离大小和X轴坐标都相等的,则对Y轴坐标进行从小到大排序;对于距离大小、X轴坐标和Y轴坐标都相等的,则按Z轴坐标进行从小到大的排序.最终得到确定的三维顶点的一维排序.从已经排序的顶点上依次提取出多组二进制信息,并做记录.计算每组数据的相关值,取最大的相关值作为实验结果.
1.3 水印检测过程
水印检测过程主要是进行相关值的计算,通过相关值来确定模型所有者的版权.

设定W'是提取出来的二进制数据,W是原始二进制数据,W'avg是W'序列中各位的平均值,Wavg是W序列中各位的平均值,N是水印序列总比特数.将随机生成的二进制数据与原始二进制数据相关值的最大相关值设定为阈值.这里所说的随机序列取得越多,取的阈值越精确.如果提取出来的二进制数据与原始二进制数据的相关值大于阈值,则可以证明模型所有者的版权;否则,则不能证明.
2 实验结果
本算法是在Matlab2010和VC++6.0的环境下实现的,主要是针对Dolphin网格模型进行实验,其中该模型共有211个顶点组成,水印信息是采用一维二进制序列.水印检测阈值的确定主要是根据相关值公式进行.为了确定阈值,首先随机生成1 000个二进制的水印信息,与原始水印信息进行比较,原始水印信息与随机水印信息的最大相关值为0.42,于是设定阈值为0.45.原始Dolphin模型和嵌入水印的Dolphin模型如图2所示.
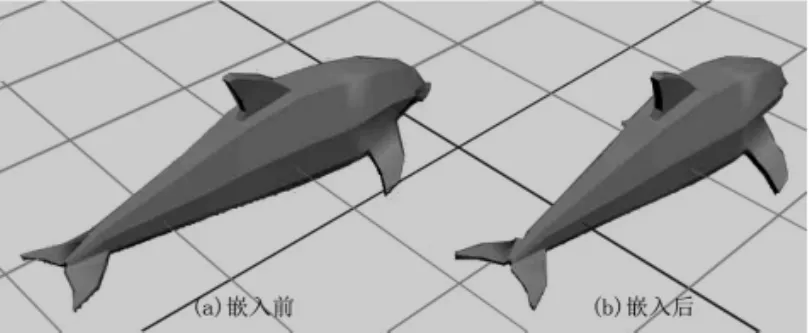
图2 嵌入水印前后的三维模型效果图
实验中,首先对嵌入水印的三维模型进行各种攻击,包括平移攻击、旋转攻击、全比例缩放攻击、单比例缩放攻击、剪切攻击、细分攻击以及简化攻击等.然后从已遭受攻击的三维模型中提取水印信息,与原始水印信息进行相关值计算.实验结果通过相关值的大小给出.
平移、旋转和全比例缩放等攻击后的测试结果如表1所示.此表包含攻击类型和相关值两列.该表中每项数据均是经过三次实验,求平均值作为实验结果.从表1可以看出,该算法针对平移、旋转和全比例缩放等攻击具有较高的鲁棒性.
单比例缩放、剪切、简化和细分攻击后的测试结果如表2所示.此表包含四大类攻击类型,每类攻击类型包含攻击比例和相关值两列.该表中每项数据都是经过三次实验,然后求取平均值作为实验结果.从表中数据可以看出,此算法的鲁棒性有待进一步加强.

表1 平移、旋转、全比例缩放攻击后的实验结果
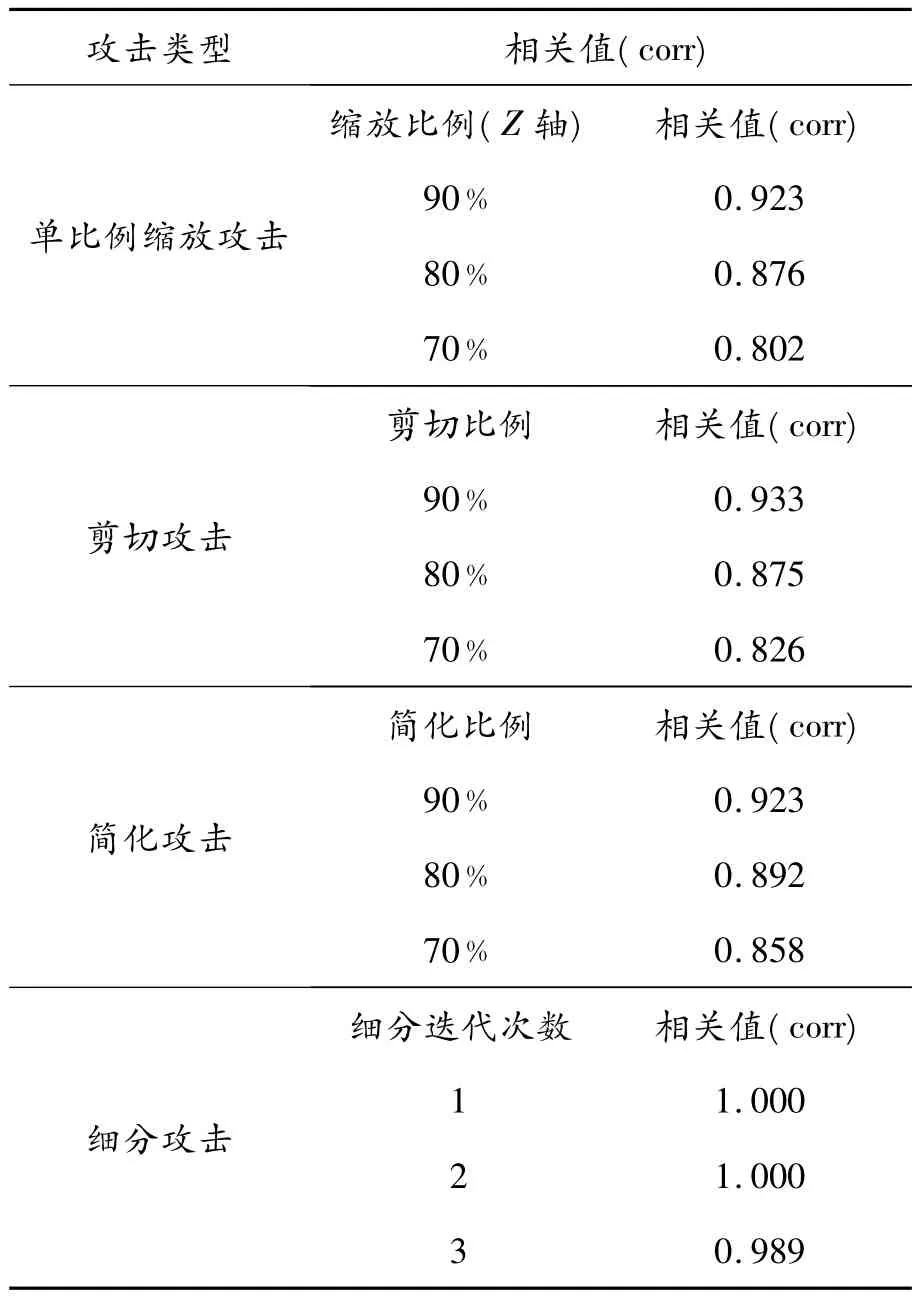
表2 单比例缩放、剪切、简化和细分攻击后的测试结果
本文算法的实验结果与文献[12]和文献[13]算法的实验结果对比如表3所示.该表针对平移、剪切、旋转、等比例缩放等攻击的相关值来进行实验结果的对比.从实验数据可以看出,本文算法针对以上各类攻击都具有较好的鲁棒性.
对于平移攻击、旋转攻击、均匀缩放攻击,由于本算法在对水印信息进行采样时会对检测模型进行重定位和重采样,将遭到攻击后的三维模型恢复到未攻击之前的位置、方向以及大小,所以本算法针对这类攻击基本上不受影响,水印几乎可以完整提取出来.
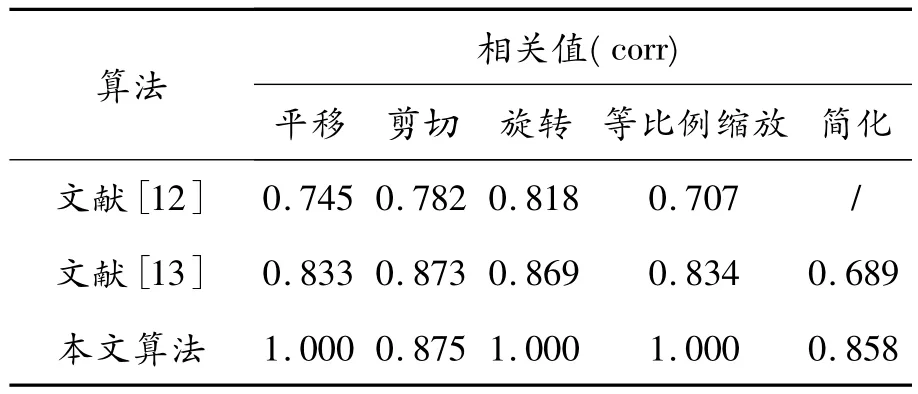
表3 文献[12]和文献[13]算法的实验结果与本文算法的实验结果对比
对于单比例缩放攻击,这里将Z轴进行单比例缩放,缩放攻击后的结果导致三维模型的一部分顶点与三维模型的中心点的距离发生了变化,导致嵌入的水印信息遭到一定的破坏,但即使遭到破坏,也远远超出实验中设定的阈值.
对于剪切攻击,对三维模型剪切的比例分别为90﹪、80﹪、70﹪.对于每次的剪切攻击,需要对三维模型进行3个不同部位的剪切,然后取平均值作为该次剪切的实验结果.相对来说,本算法针对于剪切攻击的效果不是十分理想,有待进一步加强.
对于细分攻击,本算法体现的鲁棒性还是很好的.每进行一次细分,就会在相邻的顶点之间的线上加上另外一个顶点,细分的次数越多,增加的顶点也会相应增加.但从实验结果来看,相关值还是很高的.
对于简化攻击,会对三维模型的顶点数目分别简化为原模型的90﹪、80﹪、70﹪,当三维模型简化到原模型的70﹪,该三维模型已经变得相当粗糙,基本上已经接近失去应用价值.但从三维模型提取出来的水印信息仍然远远高于设定的阈值.
从上述实验结果可以看出,本文提出的算法不受平移、旋转以及均匀缩放等攻击的影响,对于细分攻击也具有较强的鲁棒性.然而,对于单比例缩放攻击、剪切攻击以及简化攻击的鲁棒性虽然远远超过了阈值,但却不是很理想,有待进一步研究.
3 结语
本文算法在嵌入水印信息时,通过对三维模型进行定位、定向、定型,然后将水印信息加密后利用LSB的方法,多重循环嵌入到三维模型的顶点上.在进行水印信息提取时,将遭到攻击的三维模型进行重定位、重定向以及重定型,然后依次从已排序的顶点上提取水印信息,并按照水印起始标记和水印结束标记依次提取多组水印信息,然后分别进行相关值计算,取最大的相关值作为实验结果.本算法在提取水印过程中,不需要提供原始三维模型信息,属于一种盲水印算法.实验结果表明,本文算法针对平移攻击、旋转攻击、细分攻击以及全比例缩放攻击具有较高的鲁棒性,但面对单比例缩放攻击、剪切攻击以及简化攻击,虽然求得的相关值远远超过设定的阈值,但其鲁棒性却不是十分理想.因此,提高针对于单比例缩放攻击、剪切攻击以及简化攻击的能力将是进一步研究的重点.
[1]彭静,侯祥勇,马燕,等.一种自适应图像灰度水印算法[J].西南大学学报:自然科学版,2009,31(7):171-175.
[2]Wang JR,Feng JQ,Miao YW.A robust confirmable watermarking algorithm for 3D mesh based on manifold harmonics analysis[J].The Visual Computer,2012,28(11):1049-1062.
[3]Wang K,Guillaume L,Denis F,et al.Three-dimensionalmeshes watermarking:review and attack-centric investigation[J].Information Hiding,2007,67(45):50-64.
[4]唐斌,康宝宝,王国栋,等.基于三维网格模型的双重数字盲水印算法[J].计算机工程,2012,38(7):117-122.
[5]Wang Y P,Hu SM.A new watermarkingmethod for3D model based on integral invariants[J].IEEE Transactions Visualization and Computer Graphics,2009,15(2):285-295.
[6]Wang Y P,Hu S M.Optimization approach for 3D modelwatermarking by linear binary programming[J].Computer Aided Geometric Design,2010,27(5):395-404.
[7]刘晓宁,周明全.三维几何模型数字水印综述[J].计算机应用与软件,2007,24(6):14-16.
[8]胡敏,刘辉.基于特征点的自适应三维网格数字水印算法[J].合肥工业大学学报:自然科学版,2010,33(1):55-59.
[9]胡敏,谢颖,许良凤,等.基于几何特征的自适应三维模型数字水印算法[J].计算机辅助设计与图形学学报,2008,20(3):390-394.
[10]阙大顺,胡金,陈碧.基于三维网格的三维模型盲数字水印算法[J].武汉理工大学学报:信息与管理工程版,2009,31(1):1-4.
[11]王新宇,詹永照.结合顶点趋势检测的三维模型数字水印算法[J].计算机应用,2011,31(10):2665-2669.
[12]齐敬敬,顾永军,党长青.一种三维网格模型的数字水印算法[J].计算机仿真,2012,29(6):253-256.
[13]林克正,姚欢,卜雪娜.块矢量拉普拉斯矩阵的三维模型数字水印[J].哈尔滨理工大学学报,2011,16(5):113-117.
(责任编辑 穆 刚)
Three-dimensionalmodel of digital watermarking algorithm based on vertex sort
ZHAIHao1,YANG You1,WAN Hui2
(1.College of Computer and Information Science,Chongqing Normal University,Chongqing 401331,China;
(2.Scientific Research Department,Chongqing Normal University,Chongqing 401331,China)
A multiple digitalwatermarking algorithm based on the three-dimensionalmodel of vertex sort is proposed and the algorithm has significance to protect the copyright of three-dimensionalmodel.Themain idea of the algorithm is that themodel should be located,directed and shaped with the purpose of getting the initial state of three-dimensionalmodel.Then in order tomaximum improve the robust ofwatermark information,multiple cycle embed the binary watermark information in the three-dimensionalmodel using the way of LSB.Experimental results show that the algorithm own a high robustness for translation,rotation,and uniform scaling attacks.For shear attack,simplification attack and single scaling,its robustness need to be further improved.
digital watermarking;three-dimensionalmodel;vertex sort;multiple watermarking
TP312
A
1673-8004(2014)05-0128-06
数字水印技术是目前防伪及信息安全技术领域的一个新方向,它可以对各种形式的多媒体数字作品(图像、视频、音频等)的版权进行保护,即是通过在原始数据中嵌入秘密信息——水印来证实该数据的所有权[1].随着采集设备和加工技术的快速发展,三维模型被广泛应用于影视、3D游戏和文化财产的保护.在这期间,未经授权的复制、修改和传播已经变得越来越普遍.人们正面临着严峻的三维模型版权保护问题,这个问题在计算机图形学和多媒体中也是一个重要的课题[2].因此,基于信息隐藏理论的三维模型数字水印技术被提出来,该技术展示了对版权保护和所有权认证的有效方法[3].
三维模型数字水印算法的概念自从1997年由Obuchi在ACM multimedia97国际会议上提出来以后,便开启了三维模型数字水印技术的时代.第二年,以Ohbuchi为首的研究人员,提出了具有时代意义的水印算法[4]:三角形相似四元组算法、四面体体积比算法.根据不同的目的和应用,水印算法可以被分为鲁棒水印算法和脆弱水印算法.鲁棒水印算法通常是为所有者认证设计的,而脆弱水印算法[5,6]通常是为完整性认证设计的.目前,三维模型的水印算法可以分为空域水印算法和频域水印算法[7].频域算法虽然鲁棒性比空域算法高,但其复杂度较高,执行时间较长,而且嵌入容量较小.胡敏等[8]提出了一种自适应网格水印算法,该算法按模长进行分组,将每组模长进行DCT变换,然后在频域上嵌入水印信息,该算法有效解决了局部失真的问题.空域算法大多通过直接或间接修改模型坐标来嵌入水印信息,复杂度较低,嵌入容量较大,但鲁棒性不是很高.2008年,胡敏等人提出了一种基于几何特征的自适应三维模型数字水印算法[9].该算法将各顶点邻域内的顶点位置的平均差值作为掩蔽因子嵌入水印信息,可以抵抗几何攻击和抵抗部分剪切、附加随机噪声和网格简化的攻击.阙大顺等[10]提出了一种三维网格模型的数字水印算法,该算法在提取水印时要求网格顶点序号与原始水印顶点序号完全一致,极大地提高了网格顶点的识别概率.王新宇等[11]提出了一种新的结合顶点趋势检测的三维模型数字水印算法,该算法选择体现三维模型整体形状信息的顶点范数嵌入水印,通过比较待检测模型与原始模型顶点范数的变化关系,以变化趋势为依据,实现水印信息的检测.由于越靠近模型中心的顶点在遭到破坏时模型的失真率越高,上述算法都没有充分利用三维模型的自身特性.于是,一种基于顶点排序的三维模型多重数字水印算法在本文被提出来,该算法充分利用三维模型的自身特性,做到算法实现简单,复杂度低,针对各类水印攻击都具有较好的鲁棒性.
2014-01-30
重庆市教委科研项目(KJ120611);重庆师范大学横向科研项目(60102000148).
翟浩(1987-),男,山西大同人,硕士研究生,主要从事数字水印和信息隐藏技术方面的研究.
杨有(1965-),男,重庆人,副教授,博士,主要从事数字图像处理、信息安全与系统集成方面的研究.
