几何对称法在求取某些区域格林函数中的应用

罗俊芝， 杨万利， 刘艳霞

(装甲兵工程学院基础部，北京100072)

1 引 言

对于一个由曲面Γ所围成的区域Ω而言，这个区域内的狄利克雷问题

的解表示为

(1)

其中M0(x0,y0,z0)为区域Ω上的任意点，M的坐标为(x,y,z)，n为区域Ω边界的外法向量.

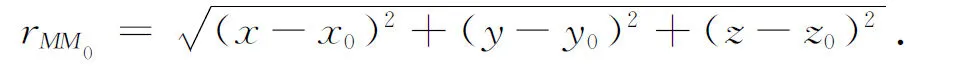
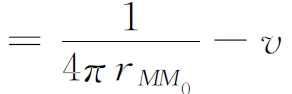
则(1)可进一步表示为

,

(2)

其中称G(M,M0)称为格林函数.

对任意函数f，上述的狄利克雷问题就转化为求此区域内的格林函数G，也就是把问题

转化为求解一个特殊的狄利克雷问题

(3)

如果把问题(3)中的v表示出来，就可以得到G(M,M0)，进而问题(1)就迎刃而解了. 格林函数法给出的解(2)是有限的积分形式，十分便于理论分析和研究.

虽然对于一般的区域Ω，求解上述问题(3)中的v并不是一件容易的事情，但是对于特殊区域上，文 [1]-[3]中利用电象法给出了格林函数的求法，该方法需要一定的物理知识作为储备，如果物理知识不熟练，可能不容易对此问题进行讨论.本文应用几何对称法研究问题(3)，进而求得格林函数.

2 几何对称法

2.1 平面对称

假设空间区域上一点M(x0,y0,z0)，则 点M关于平面的对称点为镜像对称点，如M(x0,y0,z0)关于平面z=0的对称点为M(x0,y0,-z0).设点P关于平面Ax+By+Cz=-D的对称点为M1(x1,y1,z1)，则有[5]

x1=-2A(Ax0+By0+Cz0+D)+x0,

y1=-2B(Ax0+By0+Cz0+D)+y0,

z1=-2C(Ax0+By0+Cz0+D)+z0.

2.2 球对称点

球对称点指以一个特定的球面为基础，球心O为中心, 球半径为常数k，点P和对称点P′满足

OP·OP′=k2.

利用几何对称法求取某些区域的格林函数，就是结合区域的特点，给出区域内任意点关于边界曲面的对称点，借助于几何意义，构造相应的格林函数.如果空间区域的边界曲面为平面，则利用关于平面的对称点；如果空间区域的边界曲面为球面，则利用球对称点.

下面利用几何对称法求取某些区域的格林函数.

3 半空间的格林函数

3.1 半空间区域Ω:z≥0

该区域上的狄利克雷问题对应的格林函数为

其中v为调和函数，同时v满足

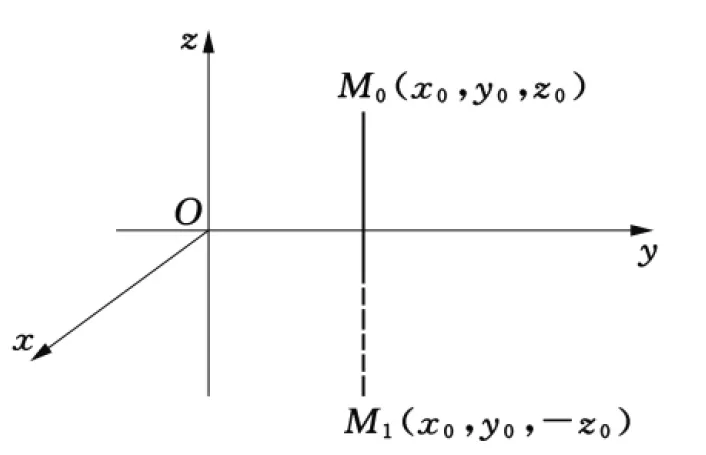
图1

根据几何知识知，

代表的是MM0两点的距离，若M取在Ω:z≥0的边界Γ:z=0时，MM0两点的距离显然与M到M0关于边界z=0的对称点M1(x0,y0,-z0)的距离相等 (图1)，所以选取

.

,

则原拉普拉斯方程或者泊松方程的狄利克雷问题

的解可表示为

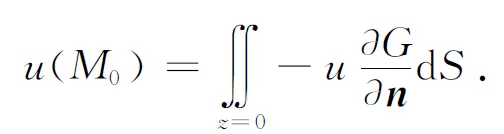
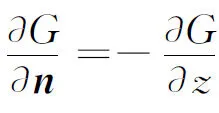
3.2 半空间区域Ω:Ax+By+Cz+D≥0

图2

所以选取

设M0关于边界平面Γ:Ax+By+Cz+D=0的对称点M1(x1,y1,z1)[5]，则通过求解有

x1=-2A(Ax0+By0+Cz0+D)+x0,

y1=-2B(Ax0+By0+Cz0+D)+y0,

z1=-2C(Ax0+By0+Cz0+D)+z0，

从而

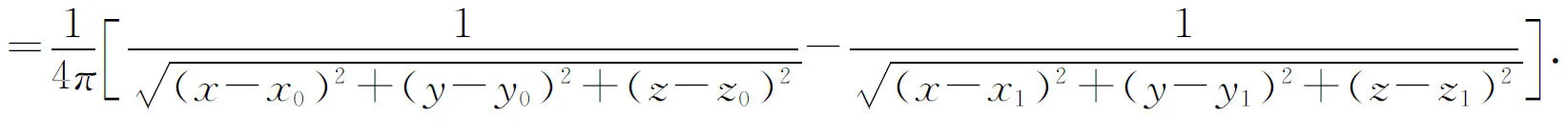
推论如果区域为平面区域Π，即Π:y≥0，边界为Γ:y=0，则平面域Π上的狄利克雷问题

因为

注意到v为调和函数且v满足

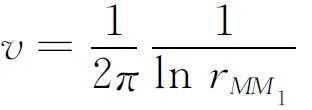
G

M

，

其中

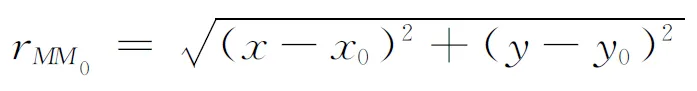
4 球域的格林函数

如果区域Ω为x2+y2+z2≤R2(图3),此区域上的狄利克雷问题为

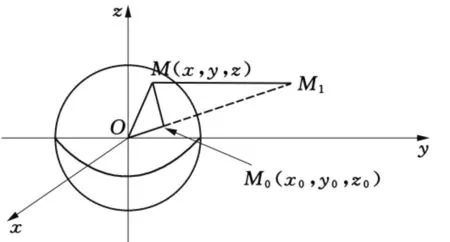
图3

因为G(M,，且v满足

首先选取M0的球对称点为M1(x1,y1,z1)(图3).

所谓球对称点满足

R2=OM0·OM1.

当M∈Γ时，

ΔOM0M～ΔOMM1.

选取

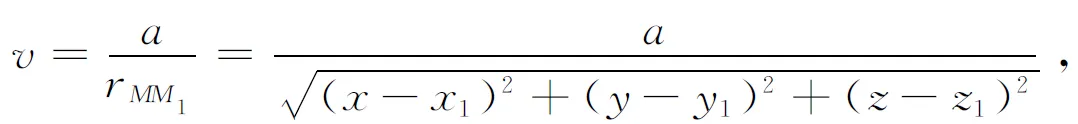
其中a为待定的常数，且满足

易见v为x2+y2+z2≤R2上的解析函数.

设∠M0OM=γ，rOM=ρ，则

格林函数

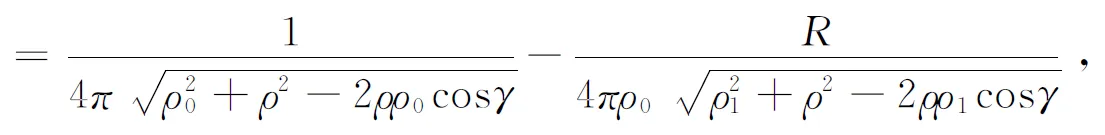
则原拉普拉斯方程或者泊松方程的狄利克雷问题

的解可表示为

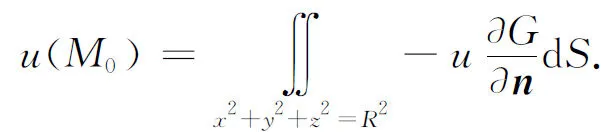
因为G的边界为x2+y2+z2=R2，故

其中n为OM的方向.从而有

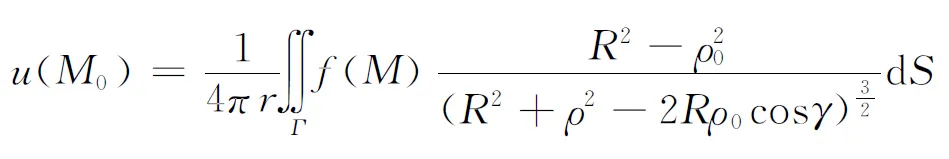
或者写成球面坐标形式

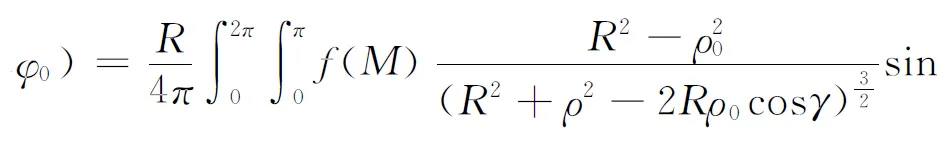
本文利用几何对称法求取特殊区域狄利克雷问题中的格林函数.对于空间区域Ω，若点P为该区域Ω的任意一点，通过点P寻找该区域上的格林函数，关键是寻找点P关于该区域边界的对称点.一般而言，如果区域是规则区域，区域内的点P关于规则区域边界的对称点需要根据区域的边界特点，如果空间区域Ω的边界曲面为平面，一般取点关于平面的对称点；如果区域Ω的边界曲面为球面，一般取点关于球面的球对称点；如果区域Ω的边界为直线，一般取点关于直线的对称点.针对不同的区域，根据几何意义，选取相应的格林函数形式，该方法与利用物理知识获得格林函数是殊途同归，这将在数学物理的学习和科研中有着很好的参考价值.

[参 考 文 献]

[1] 王元明. 数学物理方程与特殊函数[M]. 4版.北京：高等教育出版社，2012.

[2] 闫桂峰. 数学物理方法[M].北京：北京理工大学出版社，2009.

[3] 邵惠民. 数学物理方法[M].北京：科学出版社，2004.

[4] 王元明. 数学物理方程与特殊函数学习指导与习题解答[M].北京：高等教育出版社，2012.

[5] 徐沈新.三维空间中的对称问题[J].吉首大学学报( 自然科学)，1991，12(5)：23-26.

[6] 杨纪华，杨志鑫. 二维调和方程Dirichlet问题格林函数的求解[J].宁夏师范学院学报(自然科学)， 2012，33(3)：15-18.

[7] 赵天玉，刘庆.反演变换在调和函数研究中的应用[J].长江大学学报( 自然科学版)，2009，6(3):1-4.