基于支路交换法的配网重构方法分析

，，

(三峡大学电气与新能源学院，湖北 宜昌 443000)

1 引言

配电系统由于电压等级较低，线路中电流较大，使得有功损耗占全系统总损耗的比重较大，在配网中降损显得十分必要。配电系统运行优化的手段主要有：(1)网络运行结构优化；(2)无功电源运行优化。网络运行结构优化即为配网重构，通过调整联络开关和分段开关的状态改变网络拓扑，进而改变功率流动路径以降损，同时可均衡负荷，消除过载，提高供电质量，还可在恢复供电时隔离故障区域；后者指优化电容器组投切，通过采用合理电容器组配置和相应的投切策略，以满足系统部分无功功率需求，减少无功功率流动，以达到降损目的。配网系统中，配网重构目标常为有功网损最小，或者用户端的电压偏移最小，或供电可靠性最高等。一般来说，上述两种优化手段彼此之间相互联系、互不影响，为简化求解复杂度，将二者作为独立问题求解。

配网重构是一个非线性组合优化问题，原理是通过切换线路开关状态来改变网络结构,在实现电力供需平衡和满足容量、电压约束等前提下降损。然而进行配电网重构十分复杂，减小计算量，寻找全局最优解并达到优秀的收敛效果是近年来配网重构研究的热点。

2 配网重构

2.1 配网重构问题

配网重构原理[1]是在满足约束条件下，通过联络开关和分段开关的状态调整寻求一种符合要求的拓扑结构，对应目标函数常为有功损耗、能量损耗、系统负荷平衡、提高系统可靠性、提高电压水平等一个或多个目标的组合，本文以系统有功损耗最小化为例，即运行经济性，目标函数可表示：

(1)

式中，Nj和Ns分别为系统中馈线和变压器总数；pj和qj分别表示第j段线路流过的有功和无功；Vj表示第j段线路始端电压幅值；rj表示第j段线路电阻。将变压器用等值电路表示，故也可等值为馈电线路，从而计及其运行损耗。配电系统网络重构应满足以下约束条件：

(1)功率守恒约束

(2)

式中，dk为节点k的功率需求；Nn为网络中节点总数；ETk为潮流流向节点k的线路始点集合；EFk为潮流流出节点k的线路终点集合；sjk和skj分别对应流入和流出节点k的功率。

(2)容量约束

il≤IUl,l=1,…,Nf+Ns

(3)

式中，IUl为元件(线路、变压器)l的最大允许通过电流；il为元件l实际通过的电流。

(3)电压约束

ULk≤uk≤UUk,k=1,…,Nn

(4)

式中，ULk、UUk分别为节点k电压的下界和上界。

(4)拓扑结构约束

在配电系统中，由于网络辐射状运行有利于保护整定和自动化技术的实施，并能避免电磁环网，因此配电系统通常要求以辐射方式运行，即网络中每一节点k的进线(潮流流向节点k的线路)数Nin_k满足以下条件：

Nin_k∈{0,1} ,k=1,2,…,Nn

(5)

须说明一点，有分布式电源存在时，存在对负载两端供电情况，辐射状拓扑结构约束不再满足。

2.2 求解方法分析

由于配网特点，要求选取的算法能处理大规模配电系统，且计算速度快，能处理不确定信息和三相不平衡状况。传统求解方法[2]主要分为解析类方法、启发式方法、随机优化方法、智能优化方法及两种或多种算法的综合[3]等。本文通过对启发式方法中的支路交换法(Switch Exchange Method)进行介绍和改进，对交换规则进行设定，减少计算量，节省计算时间，从而能更快搜索到最优解。

3 支路交换法

3.1 支路交换法原理

在配电系统中，为保证系统的辐射状结构，闭合一个联络开关形成环路的同时，须打开环路上的一个分段开关，这样形成一个开关选择对。支路交换法的理论依据是：配电系统的可行结构为辐射状网络结构，对应系统图的一棵支撑树，如果从系统的一个可行的结构出发，选择一组开关对，闭合联络开关，打开某一分段开关，则相当于交换了二者所在的支路，即交换了支撑树中的一条链支和一条树支，从而生成一棵新的支撑树，每一步都保持网络的辐射状结构。

为减少打开候选开关数量，采用启发式规则即：认为只有当联络开关的两端存在明显的电压差，且负荷由联络开关电压低的一侧向另一侧转移时，才可能导致网损减少。

3.2 支路交换引起网损变化

在配网重构过程中，根据计算复杂性和建模需要，可选择计算网损变化量或者有功损耗，本文采用网损估计公式计算每对开关交换导致的网损变化量。

图1 两馈线系统拓扑图

以两馈线系统为例，系统拓扑如图1，假定在母线m侧和母线n侧之间连有网络开关，并配置有分段开关，由于一组负荷从m侧转移到n侧导致的网损变化为：

(6)

当具有足够优秀的无功功率补偿系统补偿无功时，可以忽略无功功率流动，式(6)中的变量可假定为实数，公式变为

(7)

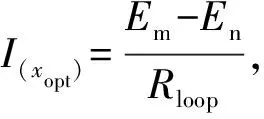
图2 网损变化量与转移负荷之间关系曲线

在考虑所有的开关交换对后，满足约束条件要求的网损降低最多的开关交换对被执行，如此往复，直到找到将网损降到最低为止。

3.3 算法及其步骤

SEM依据[4]是根据配网特点，通过选取不同分段开关，找出满足约束条件的分段开关，搜索步骤是：

(1)计算原有运行方式下(各联络开关断开，网络为辐射状)的初始潮流及网损。用恒定电流表示负荷。

(2)合上某一个联络开关相应形成一个环网，选择环网中的一个分段开关断开，使配网恢复辐射状，实现负荷转移，并估计新状态下的网损，计算潮流。在计算时，放弃不满足约束条件的分段开关操作。

(3)合上另一联络开关，重复(2)步骤并计算，直至可操作的开关均已操作完毕，从而得到网损最小的配网拓扑结构。

3.4 改进支路交换法

在支路交换过程中，每次只交换一次，然后需要对网络进行潮流计算，消耗了大量时间用于检验结果的可行性和有效性，如果能计算一次潮流后，交换一次有最大电压差的一个开关对后，接着交换一次次大电压差的一个开关对，然后再进行潮流计算，将更快寻找到最优网络拓扑结构，文中将有最大电压差的开关对交换后有最大电压差的开关对称为次最大电压差开关对，并假设支路交换前，网络参数都是满足约束条件，并且网络为辐射状结构。依据网损变化量与转移负荷之间关系曲线及其他约束条件要求，需要对该二重交换设定如下规则：

(1)将最大电压差开关对交换前，取最大电压差ΔU1，交换后，取次最大电压差，设为ΔU2。

(3)当具有次最大电压差的开关对交换后，进行潮流计算，并判断网络参数是否满足约束条件要求或网损是否增加，满足且网损减少则进行下一次支路交换，不满足或网损增加则对次最大电压差开关对交换前的网络作潮流计算，如果满足要求，则此时的网络拓扑结构为此环节最优网络结构。

须说明的一点是，此改进算法针对弱环网结构。规则中的ε可依据需要作出符合实际要求的设定，增大了人工可操作度。

4 其他算法分析

配网重构方法主要可以分为解析类方法、启发式方法、随机优化方法、智能优化方法及两种或多种算法综合求解等方法。

传统解析类方法[5]运用现有的数学优化理论与方法进行配网重构，如分支定界法[6]、线性规划方法、非线性规划以及动态规划[7,8]等优化方法。采用传统的解析类方法适用于处理系统规模不大、复杂性不高的配网重构问题，只要目标函数存在最优解就一定能够找到不依赖配电网初始结构的全局最优解，但是配网重构问题是一个 NP 难问题，单纯用传统的数学优化的方法存在着“维数灾害”的问题，并且计算量大，计算时间长，实时性不强。

应用启发式类方法时采用了近似技术和启发方式，结果容易受系统初始状态或重构过程影响，不能保证收敛于最优解。

随机优化类方法包括模拟退火算法、遗传算法、禁忌算法等。模拟退火算法[9](Simulated Annealing-SA)以一定的概率接受恶化解，使算法有机会跳出局部最优，但单纯使用SA需要大量的搜索迭代，导致计算时间过长。SA算法一般可以得到全局最优或全局次最优解，但该方法对参数和退火方案的依赖性大，计算量大，用于配网重构时需要进行多层次大量的开关交换，需要进行多次潮流计算及网损估计，计算量更大。遗传算法[10,11](Genetic Algorithm-GA)采用随即优化技术，通过模拟基因串的优者生存及随机交换信息的方法搜索优化方案，GA算法可实现内在并行计算，但计算速度比较慢，优化成果与初始基因串关联度较大。随机优化算法[12-14]和智能优化算法适于寻找全局最优解，能有效求解大规模非线性整数规划问题，但是也存在明显缺点，即收敛速度慢，耗费时间长，易产生不可行解，陷入局部解。

根据配网结构特点，将启发式算法和人工智能算法结合或许能避免两者的缺点，能有效避免陷入局部搜索，提高了计算速度。这种方法体现了人工智能算法的全局性搜索和启发式算法的快速搜索两个优点。文献[15]采取结合智能优化和启发式配网重构算法，能有效避免陷入局部解，原理在于根据初始数据选用一种速度快、收敛特性优的算法，此方法一般能获得全局解，得到较理想的重构方案。文献[16]提出了结合改进遗传算法和禁忌搜索法，将禁忌搜索法的思想运用到遗传进化的每一步,充分发挥遗传算法广域搜索优势,而且利用禁忌搜索的思想减少了很多不必要的搜索，提高了进化速度。但实际配电网包括有负荷状态、故障情况等许多不确定信息，比如负荷在一天之内不断波动，故障数据不够精确等，需要在确定性的模型中考虑不确定因素，得到更为贴近电力系统实际的结果。此类文献都旨在从计算速度和全局最优解两方面来设计算法，但不能忽视各个算法自己的缺点，对优点的凸显控制较困难，随即优化算法和智能算法因为搜索过程的随机性或对初始结构的要求，在寻优过程中不能保证收敛于最优解。

5 结束语

传统解析类方法适用于处理系统规模不大、复杂性不高的配电网重构问题，只要目标函数存在最优解，就一定能够找到不依赖配电网初始结构的全局最优解；启发式类方法普遍采用了近似技术和启发方式，结果容易受系统初始状态或重构过程的影响，不能保证收敛于最优解；随机优化和智能化方法适于寻全局最优解，但收敛速度慢，给计算机带来较大负担，从该类方法的随机性本质看，也不适于求解连续变化的大规模复杂配电网络。一般可结合解析类方法和启发式类方法可获得较好结果。我们可以结合启发式类方法和传统解析式类方法中的某两种方法，减弱两种方法的缺点，能达到更理想的配网拓扑结构。

[1]胡国伟,别朝红.一种适用于配电网重构的动态调整策略[J].西安交通大学学报,2012，46(12)：78-84.

[2]王成山，罗凤章.配电系统综合评价理论与方法[M].北京：科学出版社，2012:46-47.

[3]余贻鑫，邱炜，刘若沁.基于启发式算法与遗传算法的配电网重构[J].电网技术，2001，25(11)：19-22.

[4]许克明，熊炜.配电网自动化系统[M].重庆：重庆大学出版社,2007:101-103.

[5]陈学峰.配电网络分析及网络重构的研究[D].沈阳理工大学：2011.

[6]王守相，王成山.现代配电系统分析[M].北京：高等教育出版社.2007:146-160.

[7]刘柏私，谢开贵，周家启.配电网重构的动态规划算法[J].中国电机工程学报,2005，25(9):29-34.

[8]江东林，刘天琪，李樊.采用时段动态划分和分层优化策略的配电网重构[J].电网技术,2012，36(2):153-157.

[9]Renato CG. New method for the analysis of distribution networks [J].IEEE Trans on Power Delivery,1990,5(1).

[10]张鑫.配电网网络重构问题的研究[D].山东大学：2012.

[11]陈国良,王煦法,庄镇泉,等.遗传算法及其应用[M].北京:人民邮电出版社,1996.

[12]李聪,高睿.基于混沌遗传算法的配网重构[J].大众用电,2013(3)，29-30.

[13]毕鹏翔,刘健,刘春新. 配电网络重构的改进遗传算法[J].电力系统自动化,2002,26(2):57-61.

[14]宋平,张焰,蓝毓俊,等.改进遗传算法在配电网重构中的应用[J].上海交通大学学报，1999，33(4)：488-491.

[15]马志刚.基于遗传模拟退火算法的配电网重构研究[J].广东输电与变电技术,2010(2)：10-16.

[16]唐红键，冯可. 配网重构算法的改进和研究[J].电力勘测设计，2003(4)：53-56.