电力系统动态潮流综述

(广西电网公司崇左供电局，广西 崇左 532200)

1 引言

在常规潮流计算中，通常要假定一个Vθ节点(平衡节点)，且规定系统中的不平衡功率是由该节点吸收的。这种作法在离线应用中尚可接受。对于在线应用，系统经常会出现线路开断、发电机退出运行或负荷发生较大变化等情况，进而引起系统中较大的功率不平衡和频率的变化。这种情况下再考虑常规的潮流计算方法计算便会出现收敛性差、计算结果与实际不符。而实际的功率差额应是由多台发电机协调动作的结果，因此有必要考虑系统的准稳态过程。采用动态潮流算法，可以满足这样的计算需要。动态潮流是计算系统存在功率不平衡情况下的稳态潮流，对保证电力系统安全经济运行具有重要的理论意义和现实意义。因此，加强动态潮流的研究，深入分析动态潮流与常规潮流的异同与适用范围，提出网络拓扑对动态潮流的影响，这对电力系统的经济安全调度具有重要的理论和现实意义。

2 潮流程序研究历史与现状

电力系统潮流计算是研究电力系统稳态运行情况的一项基本电气运算，其数学本质是一组多元非线性方程，主要根据给定的运行条件和网路结构采用迭代的方法求解各母线上的电压(幅值及相角)、网络中的功率分布以及功率损耗等。且电力系统潮流计算的结果是电力系统稳定计算和故障分析的基础。电力系统潮流计算从提出至今，经历了由手工，利用交流计算台到应用数字电子计算机的发展过程。现有的潮流算法都以计算机的应用为前提，这样就为日趋复杂的大规模电力系统提供了极其有力的计算手段。经过几十年的时间，电力系统潮流计算已经发展得十分成熟，针对各种实际情况以及特殊需求，发展了多种用于电力系统潮流计算的计算机算法。

在现有的潮流算法之中，最早出现的是常规潮流算法，其他潮流算法都是根据不同的实际需求在常规潮流的基础上发展起来的。利用电子计算机进行电力系统潮流计算始于上个世纪 50年代中期，最初人们采用以节点导纳矩阵为基础的高斯-赛德尔迭代法，其原理简单，易于编程实现，同时由于导纳矩阵是稀疏矩阵，对计算机内存需求不大。但是此法收敛性较差，其迭代次数会随着系统规模的扩大而急剧增加，易出现不收敛的情况。在这种情况下，出现了基于阻抗矩阵的逐次代入法，该方法大大地改善了潮流计算的收敛性，可求解一些用导纳法无法收敛的潮流问题。但是，阻抗矩阵是满秩矩阵，不但占用计算机的内存大，且每次迭代所需的计算量也较大，这就引入了新的问题。随后发展了分块阻抗法，该方法将一个大系统分为若干小系统，在计算机内只需存储各个小系统的阻抗矩阵以及它们之间联络线的阻抗，这样不仅大幅度的节省了内存的容量，同时也提高了计算的速度。为了使潮流算法得到进一步的完善，数学中求解非线性问题的经典方法— 牛顿-拉夫逊方法被引入到了电力系统潮流计算当中。该方法以导纳矩阵为基础，有直角坐标、极坐标两种形式。自从20世纪60年代中期采用了最佳顺序消去法以后，牛顿法在收敛性、内存要求、计算速度方面都超过了阻抗法，成为直到目前仍被广泛采用的方法。此后，在牛顿法的基础上，根据电力系统的特点，抓住主要矛盾，对纯数学的牛顿法极坐标形式经过一定的简化和改进，得到了P-Q分解法 (又称改进牛顿法)。该方法以有功功率误差作为修正电压相角的依据，以无功功率误差作为修正电压幅值的依据，使有功功率和无功功率迭代分开进行，不但降低了修正方程组的阶数，而且使雅可比矩阵的元素在整个迭代过程中维持常数，不必在每次迭代时重新求解，因而在计算速度方面有显著的提高。并且由于速度上的明显优势，PQ分解法还用于在线的潮流计算。

近20多年来，潮流算法的研究仍然非常活跃，但是大多数研究都是围绕改进牛顿法和P-Q分解法进行的。此外，随着人工智能理论的发展，遗传算法、人工神经网络、模糊算法也逐渐被引入潮流计算。到目前为止电力系统发展了几十年，已经相当成熟了。随着科技水平的提高、电力系统规模的不断扩大，目前电力系统潮流计算形式分为离线计算和在线计算两种。离线计算主要用于电力系统规划设计、安排系统的运行方式，通常采用常规的潮流计算。而在线计算主要用于正在运行系统的实时监视和实时控制。常规潮流算法因其模型过于简单，不能全面考虑系统运行时多方面的实际情况，同时选择不同的发电机节点作为平衡节点亦会使所得的潮流结果存在差异，因而在线潮流计算时，通常会采用动态潮流法。

3 动态潮流的提出

常规潮流截取某一时间断面进行计算，其前提是假设系统中功率绝对平衡，全部发电机的输出功率正好等于所有负荷功率与网损之和。然而，实际的电力系统是一个动态的系统，各处的负荷时刻都在发生变化，为了达到供需平衡，系统中发电机的有功输出总体上跟随负荷的变化而变化。在电力系统中，供需恰巧平衡，不存在不平衡功率，频率不发生变化的情况是极为罕见的。通常情况下，都是供需大体平衡，系统存在着不平衡(有功)功率，这将导致系统频率发生变化。

且当系统发生供需不平衡时，系统中有一些机组具有备用容量，这些机组都有能力根据其自身的调节特性去改变其向系统注入的有功功率和无功率，同样系统负荷也会根据其自身的调节特性去改变其消耗的功率。由此可见，系统产生的差额功率应有系统中所有具有调节能力的发电机和负荷节点共同承担。所以按照这个指导思想，在潮流仿真计算中假设系统中所有节点都具有功率调节能力，当系统中出现注入停运后，所有节点都进行调节，共同承担出现的功率扰动。此时平衡节点只是系统电压的参考节点，这种假设无疑是符合实际情况的，这种潮流计算方法称为动态潮流法。

4 对动态潮流进行具体探究的新思路

4.1 动态潮流中两种不平衡功率分配思路

通过对动态潮流的分析知，当电力系统出现功率扰动后，系统中所有的发电机都将感应该扰动并调整发电机出力。在计算扰动后系统的稳态潮流时，传统的将所有不平衡功率完全由平衡节点进行平衡的潮流计算方法对该问题不能很好地解决。动态潮流计算与普通的潮流计算方法相比最大的不同即在于对以上问题的处理。当前的动态潮流计算方法在进行不平衡功率分配时主要存在两种思路，即以发电机转动惯量为依据进行分配的方法和以发电机频率特性系数为依据进行分配的方法。目前最常用的是以发电机频率特性系数为依据进行不平衡功率的分配。但是研究发现不同的分配方法都存在一定的适用条件和适用范围，且不同的分配方法对计算出的系统稳态潮流将产生影响。对于以发电机转动惯量为依据的时候，发电机转动惯量越大，其分担的不平衡功率也就越大，反之亦然。且根据发电机转动惯量进行系统不平衡功率分配的前提条件为：第一，各个节点的频率变化情况一致，且与通过系统的平均频率相等；第二，发电机调速设备未启动。而对于以发电机频率特性系数为依据的时候，发电机频率特性系数在系统等值机的频率特性系数中所占的比例越大，其所分配到的不平衡功率也越大，反之亦然。该结果的推导过程中，忽略了系统出现扰动到系统内发电机动作后使系统进入稳态之前的系统动态过程。且对发电机的调速设备仅考虑了其静态频率特性系数，而对不同发电机所包含的不同类型的调速器及原动机的“传函”差别并未进行考虑。如对汽轮发电机的再热环节，水轮发电机的水锤效应；最后为了使系统内的发电机对不平衡功率的分担量与其自身的可调节情况相一致，在对各台发电机的频率特性系数进行整定时应该考虑各台发电机的配合问题。

4.2 基于动态潮流的节点类型的新定义与分析

为了说明和描述的方便，下文物理量上面带有“～”的表示该物理量允许在一定的范围内调整，如：

常规潮流算法中有Vθ、Pv和PQ三种节点类型。通常将调频发电机节点定义为Vθ节点，该类节点的电压幅值和相位已知(兼有系统相位参考节点的作用)，而其有功功率和无功功率视系统的功率平衡情况而定，属于待求的未知量。在常规潮流算法中，通常只设1个Vθ节点，其余发电机节点可以定义为Pv节点，部分发电机节点也可以定义为PQ节点，负荷节点和联络节点一般定义为PQ节点。

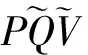
动态潮流算法的节点类型是对普通潮流算法的节点类型的联合拓展，依据拓展类型求得的各变量结果在本质上符合普通潮流对相应变量的要求。这也从侧面说明了动态潮流算法在一定程度上保持着普通潮流的特性，但也是对普通潮流的改进。

4.3 求解动态潮流的具体思路

由实际和仿真结果可知，当系统总发电机功率大于系统总负荷与总网损之和时，这部分不平衡功率将使系统频率升高，反之则减小。因此在计算动态潮流时，可由迭代计算出的系统网损来计算出系统的不平衡功率，再由不平衡功率计算出系统的频率的变化量。利用动态潮流计算方法在电网调度仿真机上进行潮流计算结果表明，动态潮流方法具有P-Q分解法的所有优点，其收敛速度至少和它相同，甚至更快，特别是在系统出现大的扰动时，其收敛性远好于P-Q分解法。

5 结论

动态潮流和常规潮流的主要区别在于发电机的有功出力不再是定值，在计算过程中它是随着不平衡功率的变化而变化的。这一不平衡功率在常规潮流中是由平衡节点的发电机承担，而动态潮流是将不平衡功率分散到系统中所有具有功率调节能力的发电机和负荷去承担，计算结果更符合系统实际情况。两者的方程个数是一样的，只是动态潮流在计算节点有功功率偏差量时应考虑发电机的功率的变化。另外，动态潮流还考虑了系统频率和功率不平衡量的关系。因而动态潮流对电网的实际调度具有重要意义。由于动态潮流是在常规潮流基础上的改进，因而也保留了常规潮流的许多东西，例如节点导纳矩阵。又因节点导纳矩阵的形成与系统的网络拓扑有关，因而有必要进一步探究网络拓扑的变化(如系统的解裂、并网等)对动态潮流计算的影响。

[1]王锡凡.现代电力系统分析[M].科学出版社,2003,3:1-5.

[2]张伯明,陈寿孙.高等电力网络分析[M].北京:清华大学出版社,1996.

[3]吴水军,束洪春,董俊,等.动态潮流中两种不平衡功率分配方法的比较[J].云南电力技术,2006,34(2).

[4]王志勇,崔秀玉.南方电网交直流混合输电系统动态潮流仿真计算[J].电力系统自动化,2005,29(17).

[5]余小燕,于继来.基于有功无功联合调整的动态潮流[J].电网技术,2005,29(22).

[6]孙雪景,张永,魏立明,等.基于动态潮流的输电网损耗计算与影响分析[J].吉林电力2009,37(6).

[7]Serrano B R,Vargas A.Active-reactive power economic dispatch of very short term in competitive electric markets[A].Power Tech Proceedings[C].Portro:2001 IEEE,2001.

[8]王永刚,韩学山,柳焯.动态优化潮流[J].中国电机工程学报,1997,17(3):195-198.

[9]Salamat SharifS,Taylor J H,Hill E F,et al.Real-time implementation of optimal reactive power flow[J].IEEE Power Engineering Review,2000，20(8)：47-51．

[10]Rueda S M V,Almeida K C.Optimal powerflow solutions under variable load conditions:reactive power cost modeling[A].IEEE Power Industry Computer Applications Conference [C].Sydney,NSW:Institute of Electrical and Electronics Engineers Inc.22-24 May 2001,300-305.

[11]廖华兴,刘宝柱,于继来.基于规则的无功潮流调整方法[J].中国电力,2004,37(2):40-44.

[12]郎兵.动态潮流模型在电网调度仿真系统中的应用[J].北方交通大学学报,2002,26(4):83-87.