基于交货期的跨组织资源服务链调度研究

王正成，咸 达

（浙江理工大学经济管理学院，杭州 310018）

基于交货期的跨组织资源服务链调度研究

王正成，咸 达

（浙江理工大学经济管理学院，杭州 310018）

为克服跨组织资源服务链中某个资源服务企业的不确定性，导致在规定的交货期内没有完成生产任务，从而使整个服务链的生产周期受到影响的问题，提出了资源服务的替代性调度和协作性调度，构建了在交货期内，使得时间最短和时间成本综合最优的数学模型，并针对该问题模型利用粒子群算法进行求解。最后通过一个仿真跨组织资源链调度算例，并根据数学模型和用粒子群算法求解，分别获得了算例基于替代性调度和协作性调度的方案，验证了这两种调度模型的有效性和可行性。

资源服务链；交货期；仿真调度；数学模型

一、问题描述及模型建立

跨组织资源服务链是指服务于跨组织协同制造总任务根据产品形成过程分解形成的时序与约束关联的一系列原子任务执行过程中的各种制造资源所构成的资源有向网络结构。关于服务链的构建问题，本文不再阐述，可以参考文献［9］，跨组织资源服务调度问题是当服务链中某企业无法完成原本规定的生产任务，必须将未完成的生产任务立即调度给其他企业进行生产，反应了企业快速决策的变化过程，是动态多变且复杂的，很难用统一的数学模型加以描述，不失一般性，本文通过对问题本质的分析，将问题简化，并做如下假设：

a）跨组织资源服务链已经构建完成，每个资源企业按照其规定的时间进行生产加工，必须按照一定的时序执行，生产和运输调度是在接到订单后进行的；

b）本问题不考虑企业内部生产线上的作业调度，不考虑订单分类问题；

c）运输的批次，车辆的装载及交货的时间与成本计入到运输时间和运输成本中；

d）当某资源服务企业发生突发状况时，对其已经完成的部分产品将运输到与其联结的资源服务企业，此时的运输时间，成本不考虑到问题模型中。

本文的问题描述如下：某制造总企业经过综合考虑，已经构建好的一条服务链中共有m个资源服务企业，资源服务企业的集合记作R＝｛R1，R2，…Rm｝。资源服务企业Ri的交货期时间为Ti0，资源服务企业Ri将生产的产品交付给与其有联结关系的资源服务企业Rj的规定时间为Dij，Ri与Rj之间的运输时间为Tij，运输成本为Cij（i∈［1，m］，j∈［0，ri］），其中ri为资源服务企业Ri与拥有联结关系的资源服务企业Rj的数量。若某一资源服务企业Ri由于突发情况导致无法完成的生产任务量为Si（i∈［1，m］），与其进行生产调度的候选资源服务企业集合为X＝｛X1，X2…Xn｝，n为候选企业的数量。其中Ri对Xk进行生产调度方案集合为Yk＝｛（t1，p1）…（ta，pa）…（tuk，puk）｝，ta，pa分别为候选企业进行实行调度方案的生产时间，生产批量，生产成本为C′a，uk为调度方案集合的数量（a∈［1，uk］）。Ri与Xk之间的运输时间为Tik，运输成本为Cik，Xk与Rj之间的运输时间为Tkj（k∈［1，n］，j∈［0，ri］），运输成本为Ckj，企业将如何选择调度决策，使其在交货期内，时间最短和时间成本综合最优。定义决策变量为xika＝1，表示问题企业Ri将生产任务调度给Xk并采取第a种调度方案进行生产，否则xika＝0。

（一）替代性调度

在现实生活中，制造总企业与服务链上的各个资源企业相互合作、相互协调，但是由于其中某个企业无法完成生产任务，可能会失去信誉，导致制造总企业不再与其合作，直接将其生产任务调度给其他候选企业进行生产和运输。替代性调度是指该问题企业不再参与生产，要将未完成生产任务调度给其他候选的资源服务企业。假设问题企业为R1，由于某种原因，例如厂房倒塌，机器损坏，资金不充足导致无法在规定的交货期内完成生产任务，因此将其生产资源调度给与其有合作关系的候选企业｛X1，X2，…，Xn｝，并选出几家企业帮助其生产，而在资源服务链中，R1需要将生产的产品交付给与其有联结关系的资源服务企业｛R2，R3，…，Rri｝，此时则由候选企业｛X1，X2，…，Xn｝将产品交付给企业Rj，从而保证整体的跨组织资源服务链的企业生产时间按时完成，替代性调度过程如图1所示。

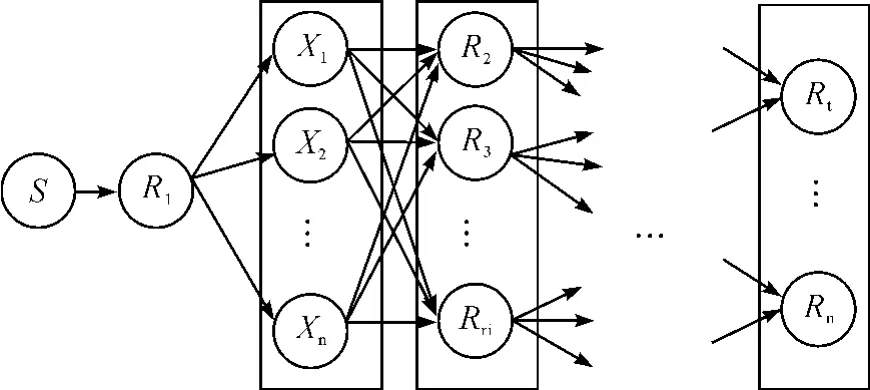
图1 跨组织资源服务链替代性调度示意图

1．替代性调度模型

跨组织资源服务链调度时间的构成主要是由Ri调度给Xk的运输时间，Xk的生产加工时间，Xk与Rj之间的运输时间（i∈［1，m］，k∈［1，n］，a∈［1，u］，j∈［0，ri］）。因此定义替代性调度基于交货期时间内的目标函数为：

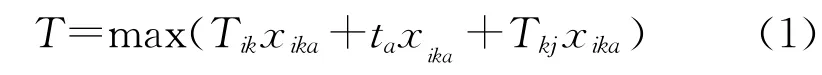
同样，跨组织资源替代性调度基于成本的目标函数构成主要是调度给资源服务企业的生产成本和运输成本，目标函数为：

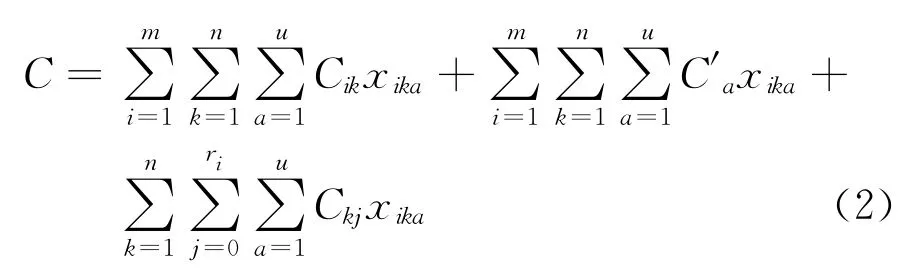
综合式（1）和式（2），替代性跨组织资源服务链调度基于时间和成本综合最优的数学模型为

这是一个多目标函数优化问题，其中μ1和μ2分别为时间和成本所占的权重比例，在企业的实际运作中，由于必须在交货期内完成生产任务，而只考虑时间，不考虑成本时，则μ2＝0。式（4）是指调度的资源服务企业所完成的生产批量；式（5）表示必须在交货期内完成生产任务。

（二）协作性调度

协作性调度是与替代性调度相对立的，指问题企业还可以继续生产，但生产批量有所减少，并且也调度给其他企业生产任务，协作性调度的过程如图2所示。假设问题企业为R1，由于某种原因，例如车间生产安排不当，导致不能够在规定的交货期内完成生产任务，需要将生产资源调度给与其有合作关系的候选企业｛X1，X2，…，Xn｝，同时企业本身也继续生产，这种情况下，企业｛X1，X2，…，Xn｝要将生产的产品和R1生产的部分产品在规定的交货期内交付给与R1有联结关系的资源服务企业｛R2，R3，…，Rri｝

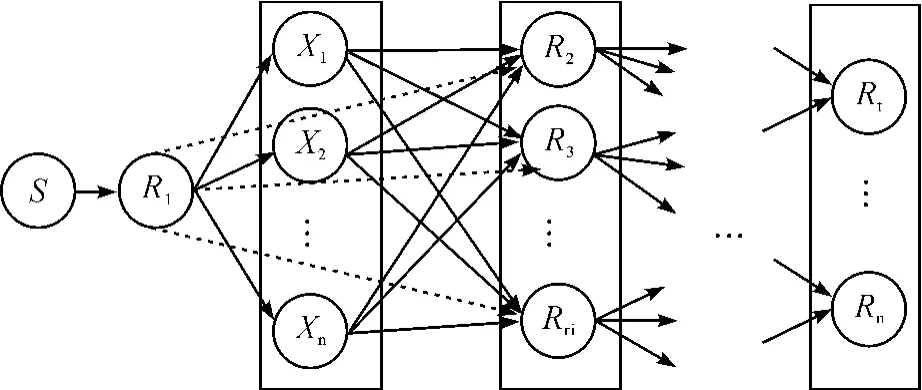
图2 跨组织资源服务链协作性调度示意图

1．协作性调度模型

跨组织资源服务链协作性调度的时间构成是在替代性调度的时间构成基础上增添了问题企业自身的生产时间，当然这里的生产时间不是该资源服务企业出现问题之前的生产时间，而是出现问题之后，还能继续生产加工的时间，设为Ti，生产成本为Ci，生产批量为Qi，因此定义协作性调度基于交货期时间内的目标函数为：

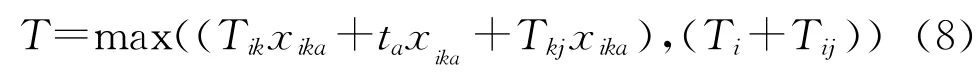
同样，跨组织资源协作性调度目标函数可以表示为：

综合式（8）和式（9），协作性跨组织资源服务链调度基于时间和成本综合最优的数学模型为

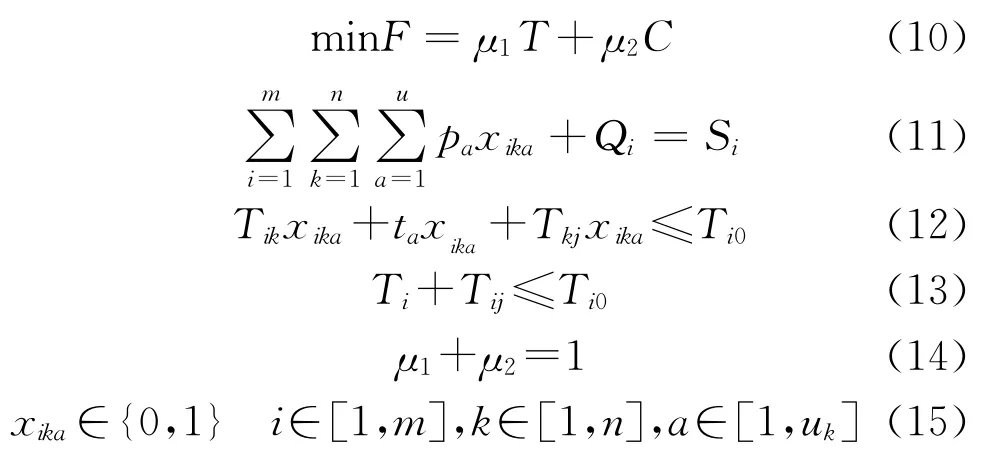
二、算法与仿真算例

（一）二进制粒子群优化算法

二进制PSO（binary particle swarm optimization，BPSO）算法［10］是由 Kennedy和Eberhart在基本PSO算法的基础上提出的。BPSO是一种基于群体智能的优化技术，概念简单，容易实现，参数少，收敛速度快，对于求解离散组合优化问题，有非常好的效果。本文针对跨组织资源服务链调度模型，将该算法与调度问题相结合，进行求解。其中d＝1，2，…，D；i＝1，2，…，n；t为当前迭代次数分别为最小和最大速度，w为惯性权重；c1，c2为加速度因子，为非负的常数；r1，r2，ρ是分布于［0，1］之间的随机数。是神经网络中常用的一种模糊函数Sigmoid，其表达式为：

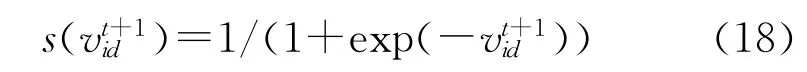
（二）粒子位置编码

BPSO中每个粒子的位置矢量属于二进制空间（由0和1组成的二进制字符串），也就是均只能取0或1，而在该跨组织服务链调度模型中，问题企业要选出最优的调度方案，相当于粒子在多维空间进行搜索，每个粒子的位置是由0和1组成，将决策变量xika构造成0，1编码的粒子，则xika表示粒子群中第i个粒子的位置值，粒子i的位置可以表示为xika＝（xik1，xik2，…xikuk），xika＝1表示问题企业Ri将生产任务调度给Xk采取第a种调度方案进行生产，否则xika＝0。粒子的适应度值则为目标函数值。

例如，有1个问题企业，该企业需要与4个候选企业进行调度，候选企业1有2种调度方案，候选企业2有3种调度方案，候选企业3有4种调度方案，候选企业4有2种调度方案，其中选取了候选企业1的第1个调度方案，候选企业2的第2个调度方案，候选企业3的第3个调度方案，候选企业4的第2个调度方案，则此时的粒子的位置编码如图3所示。此时粒子的编码位置x＝｛10010001001｝。

图3 粒子位置编码构造图

（三）粒子的参数设置

在BPSO算法中，惯性权重w决定了粒子先前速度对当前速度的影响程度，直接关系到BPSO算法的搜索能力与收敛速度，当惯性权重较大时，有利于全局搜索，且收敛速度快，但不易得到精确解；当惯性权重较小时，有利于局部搜索，但容易陷入局部最优解。本文的w采用线性递减策略，公式为：

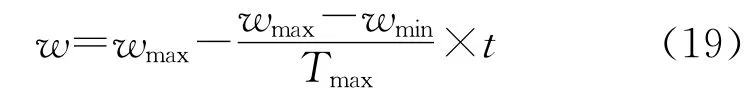
其中，wmax，wmin分别为惯性权重的最大值和最小值，Tmax为最大迭代次数，t为当前迭代次数。并将粒子的初始速度设为：

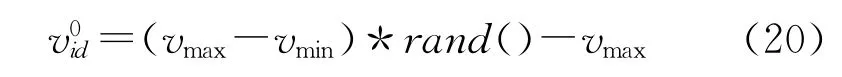
这样在迭代开始时，粒子先进行全局搜索，找到最优解的大致位置，随着w的减小，粒子速度减慢，并进行局部搜索，寻找精确的最优解。

如果粒子的速度超出vmax，可能会使粒子飞过最优解，若粒子的速度太小，则导致粒子收敛速度过小，可能只找到局部最优解，无法找到最优解，因此对超过［vmin，vmax］的粒子速度，则按照公式（21）进行修正。

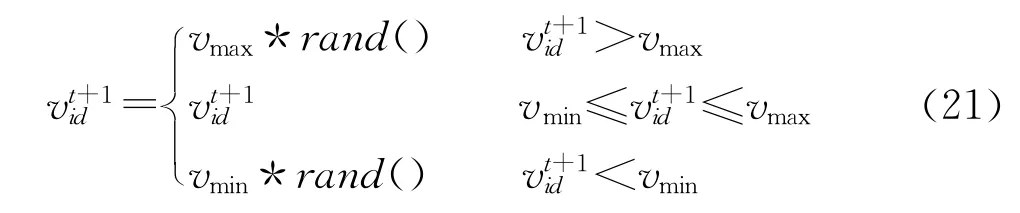
（四）算法步骤

利用粒子群算法求解调度模型的步骤如下：

a）确定种群规模，学习因子，速度，采用标准粒子群算法参数进行设置，并按照本文提出的粒子位置编码原则随机产生粒子的位置。

b）根据适应度函数，也就是本文中的目标函数，计算各个粒子的适应度值，将各个粒子的位置与适应度值存储在个体极值中，将种群中适应度值最优的粒子个体位置和适应度存储在全局极值中。迭代次数t＝1。

c）利用式（16）和式（17）对速度和位置进行更新。

d）更新速度和位置后，利用适应度函数重新计算各个粒子的适应度值；并更新个体极值和全局极值。

e）令t＝t＋1；查看是否满足最大的迭代次数T，不满足重复步骤c）～e），满足则迭代终止，输出群体中最优的粒子位置与全局极值。

（五）算例仿真

本文假设有一跨组织资源服务链，如图4所示。有6个企业进行生产，其中R2企业在生产上出现了问题导致不能在交货期内完成生产任务，现设R2要完成的产品数量为1 000件，交货期为20天，如果继续让R2进行生产，在交货期内最多生产200件。制造总企业得知后，准备对R2企业进行生产调度，现有3家企业X1，X2，X3可以完成，每家企业的生产时间（天），生产数量（件），生产成本（万元）的参数如表1，与R3，R4的运输时间，运输成本如表2所示。

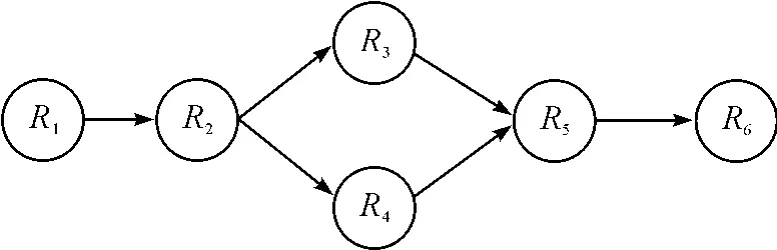
图4 跨组织资源服务链示意图

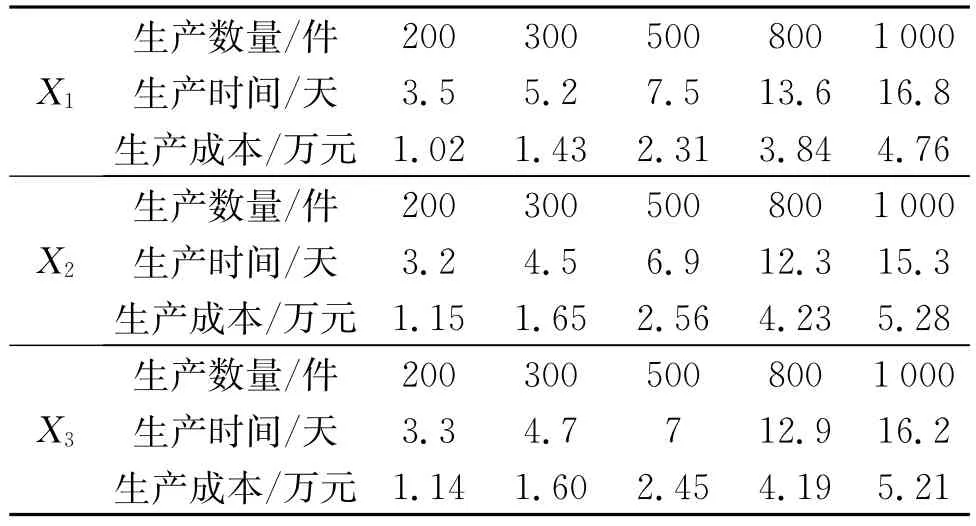
表1 企业的调度方案参数表

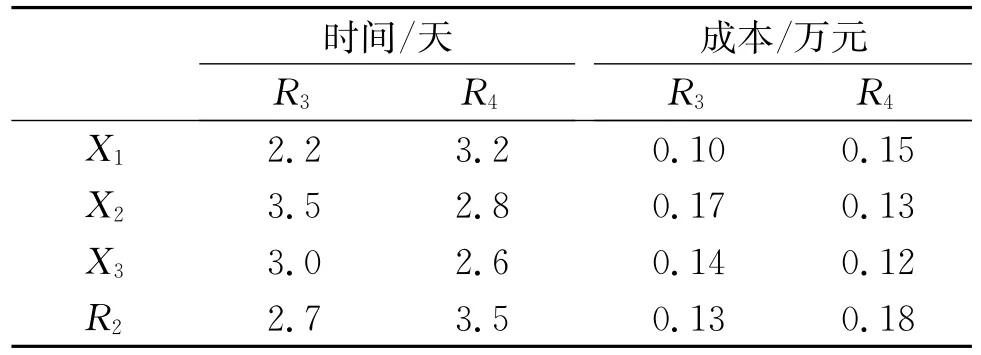
表2 企业间的运输时间与运输成本

最后通过MATLAB平台进行仿真计算，利用粒子群算法进行求解，设置初始参数，粒子数为30，迭代次数为200，学习因子c1＝c2＝1．494 45，wmax＝0．9，wmin＝0．4；vmax＝6，vmin＝－6；μ1＝0．7，μ2＝0．3；分别对跨组织资源服务替代性调度和协调性调度进行求解，计算得到替代性调度基于时间最短的方案应选择X2，X3分别生产500件产品，总时间为10．4天；基于时间与成本综合最优的方案应选择X1，X3分别生产500件产品，综合最优值为23．3，其中时间为10．7天，成本为5．27万元。协作性调度是基于R2自身生产200件的基础上，对未完成的800件进行调度，基于时间最短的调度方案为企业X1生产200件，X2生产300件，X3生产300件，时间最短为8天；基于时间和成本最优的方案为X1生产300件，X3生产500件，综合最优值为24．4，其中时间为10天，成本为5．8万元。

三、结束语

本文通过对跨组织协同制造资源服务链调度进行研究，构建了以时间和时间成本综合最优的数学模型，并提出了替代性调度和协作性调度两种调度方式，并利用二进制粒子群算法进行求解，提出了粒子的编码方法，将问题模型与算法相结合，最后通过仿真算例验证了两种调度方法的有效性，为解决跨组织协同制造资源服务链调度问题提供了一种切实可行的方法。

本文的研究是基于现实的可行性假设下进行的，而在实际的跨组织资源服务链调度中，要考虑很多因素，如质量、库存成本、风险因素［11］、运输批次、订单分类等，这些因素都影响着整个全局最优的跨组织资源服务链调度，而且由于企业间竞争激烈，信息不完全共享［12］，内部外部环境的快速变化，要想建立一种将所有基本因素都考虑进去并实现全局最优的资源服务链调度也是非常困难的。本文是在制造企业进行服务链调度时，将问题抽象化，由于要保证在交货期内完成生产任务，因此时间是必须保证的条件之一。当然由于每个企业作为首选的评价指标可能各不相同，因此本文所涉及的数学模型具有一定的局限性。但是不失一般性，为跨组织资源服务链调度问题提供了一种有效的解决办法。

［1］Yeung W K，Choi T M，Cheng T C E．Optimal scheduling of a single－supplier single－manufacturer supply chain with common due windows［J］．Automatic Control，IEEE Transactions on，2010，55（12）：2767－2777．

［2］Ivanov D，Sokolov B．Dynamic supply chain scheduling［J］．Journal of Scheduling，2012，15（2）：201－216．

［3］蒋大奎，李 波．基于禁忌搜索的平行机多工厂供应链调度［J］．中国机械工程，2012，23（6）：688－693．

［4］王建华，李 南，郭 慧．基于时间槽的敏捷供应链集成调度模型及优化［J］．系统工程理论与实践，2011，31（2）：283－290．

［5］但 斌，肖 剑，刘晓红，等．基于交货期窗口约束的多级供应链批量调度问题研究［J］．计算机集成制造系统，2007，13（2）：310－316．

［6］谢志强，常宁宁，杨 静．基于交货期紧迫度的综合调度算法［J］．机械工程学报，2011，47（22）：181－190．

［7］刘 琳，谷寒雨，席裕庚．一种基于分解交货期的Job Shop启发式调度算法［J］．控制与决策，2006，21（3）：253－257．

［8］Sawik T．Coordinated supply chain scheduling［J］．International Journal of Production Economics，2009，120（2）：437－451．

［9］王正成，潘晓弘，潘旭伟．基于蚁群算法的网络化制造资源服务链构建［J］．计算机集成制造系统，2010，16（1）：174－181．

［10］Kennedy J，Eberhart R C．A discrete binary version of the particle swarm algorithm［C］／／Systems，Man，and Cybernetics，1997．Computational Cybernetics and Simulation．，1997 IEEE International Conference on．IEEE，1997，5：4104－4108．

［11］Finke G R，Schmitt A J，Singh M．Modeling and simulating supply chain schedule risk［C］／／Simulation Conference（WSC），Proceedings of the 2010 Winter．IEEE，2010：3472－3481．

［12］孙 靖，林 杰．信息不完全共享下MC供应链动态调度模型研究［J］．系统仿真学报，2007，19（9）：1943－1948．

（责任编辑：陈和榜）

Research on Cross－organizational Resource Service Chain Scheduling Based on Time of Delivery

WANG Zheng－cheng，XIAN Da
（School of Economics ＆ Management，Zhejiang Sci－Tech University，Hangzhou 310018，China）

To overcome the uncertainty of some resource service enterprise in cross－organizational resource service chain which will cause the failure to complete productive task within the specified time of delivery and influence the production cycle of the whole service chain，this paper puts forward alternative scheduling and collaborative scheduling of resource service，establishes a mathematical model realizing the shortest time and optimal time cost within the time of delivery，uses particle swarm algorithm to solve the problem，respectively obtains programs of the case based on alternative scheduling and collaborative scheduling through a simulated cross－organizational resource chain scheduling case according to the mathematical model and particle swarm algorithm and verifies the validity and feasibility of both scheduling models．

resource service chain；time of delivery；simulation scheduling；mathematical model

1673－3851（2014）02－0013－05

TP165；TH166

A

随着全球化经济的快速发展，利用网络优势，协同网络制造资源组成的跨组织资源服务链是制造业发展的必然趋势。在跨组织资源协同与共享过程中，由于资源服务企业可能出现一些突发情况，如费用超支、机器故障、任务安排不当等因素影响，导致任务无法在规定的时间内完成，从而影响整条服务链的生产周期安排。为使跨组织资源服务链上的资源服务企业在其各自的交货期内交付任务，必须对每个企业进行监控处理。一旦某个企业出现上述问题，应立即对其进行生产调度，快速响应内部与外部环境的变化，从而对整个资源服务链进行重构、调整。

当前对跨组织资源服务链的调度研究，主要还是停留在企业内部生产工序的安排调度、供应链的生产调度和运输调度。如Yeung等［1］研究了基于交货期窗口约束的单一供应商、单一制造商和多个零售商间的供应链调度问题，并将其转化成flow shop调度问题，并利用多项式算法进行优化和求解。Ivanov等［2］将现代优化控制理论和运筹学研究方法解决动态性供应链调度问题，建立了动态供应链调度的生成和执行控制流程模型，并进行了实验验证。蒋大奎等［3］提出一类平行机多工厂供应链调度问题，以生产和运输总成本为最小化目标，利用禁忌搜索算法求解该问题。王建华等［4］建立了基于时间槽的敏捷供应链集成调度INLP模型，有大量的时间和数量约束，并设计了混合遗传算法进行求解。但斌等［5］综合考虑了在交货期窗口约束下，供应商与制造商的库存成本、运输成本、未按期交付的惩罚成本，并建立了多级供应链批量调度模型。供应链调度问题只需要考虑供应商与制造商之间的相互影响因素，而在实际的跨组织资源服务链中，每一个资源服务企业既是供应商又是制造商，并且在交货期时间内要对复杂产品进行综合调度［6］和车间内工件在机器上生产进行调度等［7］，考虑的因素复杂多样［8］，采取的调度方法也不尽相同。

跨组织资源服务链是动态、复杂和基于时序的有向网络图，调度的关键是如何安排生产任务和运输任务，使得在交货期内运输到下游企业，保证后续的加工路线得以延续。本文对无法在交货期内完成生产任务的某个资源服务企业进行替代性调度和协作性调度，并分别建立了基于时间、时间和成本综合最优的数学模型。最后通过仿真算例验证了模型和算法的可行性和有效性，为跨组织资源服务链调度问题提供了技术和方法支撑。

2013－10－09

国家自然科学基金资助项目（71271192）；浙江省自然科学基金资助项目（LY12G01008）；浙江省科技厅公益计划项目（2013C31016）

王正成（1974－），男，副教授，博士后，主要从事方向电子商务、先进制造模式方面的研究。

咸 达，E－mail：achengwang＠163．com