居民生活满意度评价模型及参数估计

张志英

（浙江理工大学数学科学系，杭州 310018）

居民生活满意度评价模型及参数估计

张志英

（浙江理工大学数学科学系，杭州 310018）

居民生活满意度是社会和心理学研究的重要内容之一，而满意度评价模型的建立、检验和参数估计又是其中的难点和重点问题。文章以结构方程模型理论为基础建立城镇居民生活满意度的测量模型，通过问卷调查获取样本数据，并用偏最小二乘法估计模型参数。研究表明，与居民生活满意度有关的因素中，居民自身身体活动能力与居住环境的安全性影响较显著，而物质条件好坏影响不大；家庭内部状况对生活满意度的影响力稍大于工作状况的影响力；居民生活态度积极与否、对未来是否充满信心也是影响生活满意度的重要因素。

居民生活满意度；结构方程模型；偏最小二乘法（PLS）；问卷调查；参数估计

生活满意度是心理学和社会学中非常重要的内容之一，它是衡量一个国家或者地区的居民生活质量的主要参数之一。目前对满意度的研究大多集中在企事业单位、政府部门、服务部门的顾客满意度方面。按照不同的学科，研究的思路和方法也不同，有的是从管理学方面来确定满意度的影响因素以及它们的权重，利用的方法包括专家打分法、层次分析法（AHP）等，有的是从消费心理学方面通过问卷调查的方法获得满意度影响因素的权重［1－3］。

对于生活满意度的评价不能只局限于主观的定性测评，如果要从定量角度衡量生活满意度，就必须建立量化模型。除了涉及可直接观察的变量（如居民收入、居民寿命等）之外，还包括许多潜在变量（居民心理感知、生活压力等），这些潜变量与可观察变量之间的关系是研究的难题。就我们所了解的，现在已经建立了完善的生活满意度计量模型的国家有很多，比如欧盟的一些国家以及美国等发达国家，在注重环境保护、重视生活舒适度的挪威和瑞典等国家也提出了相应的生活满意度评价模型［4－5］。

借鉴顾客满意度研究的方法和思路，对于居民生活满意度的评价我们采用结构方程模型来研究，并采用适合问卷调查样本数据特点的偏最小二乘法（PLS）估计模型的参数。通过该模型将生活满意度指数和几个潜在变量以及几个可观察变量联系起来。这样的研究方法有助于适时了解居民生活满意度，寻找影响居民满意度的重要因素，进而改善生活环境，提高居民生活质量，这都是构建和谐社会推进国家和地区协调发展的重要环节。

一、结构方程模型

结构方程模型（Structural Equation Modeling，简称SEM）是当代行为与社会领域量化研究的一项重要的多变量统计分析技术和研究方法，融合了传统多变量统计分析中的“因素分析”与“线性模型回归分析”的技术，被广泛应用在多个学科领域中［6］。

（一）SEM基本原理

SEM包括两个基本模型（一是测量模型，一是结构模型）和两组基本变量（一是潜在变量，一是观察变量）。

测量模型是反映潜变量与观察变量之间的互变效果，有两个方程：

该方程规定了内生潜变量ηm×1与内生观察变量Yp×1之间的互变效果。

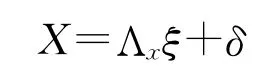
该方程反映的是外生潜变量ξn×1和外生观察变量Xq×1之间的互变效果。

方程中Λy和Λx都是因子负荷，εp×1和δq×1表示误差。

结构模型为：η＝Bη＋Γξ＋ζ，反映潜变量之间的连结关系，其中，Bm×m与Γm×n都是因子负荷，ζm×1是残差。

通过上面两组方程，可以求得模型假设下的协方差矩阵∑，再设S表示通过原始数据计算的样本协方差矩阵，那么，通过比较∑与S之间的差异大小可以对模型进行检验和评价。

（二）模型参数估计的基本方法

结构方程模型参数估计基本思路是试图使得样本协方差S减去被预测的协方差∑所形成的残差最小化。

在SEM分析中，提供的参数估计方法有很多，研究中广泛使用的是极大似然估计法（Maximum likelihood，ML）、一般化最小平方法（General least squares，GLS）、加权最小平方法（Weighted least squares，GWLS）以及偏最小二乘法（Partial least squares，PLS）。

ML方法的使用很普遍，LISREL（Linear Structural Relations）软件就将这种方法作为预设的模型估计方法，这种方法适合用在持续以及非对称的大样本上，并且假设观察变量是独立、符合多元正态性的时候，卡方检验才能合理使用。如果数据是小样本，或者虽然是大样本，但是不符合多元正态性假定，此时选用GLS或者PLS比较合理［6］。

在此次研究中，因为受到人力物力的影响，通过问卷调查收集到的居民生活满意度数据样本容量比较小，观察变量很难满足正态分布，并且靠研究者主观选取的指标之间的关系还不是非常确定，预计的分析结果中也需要得到潜变量的分值，所以最终决定采取PLS方法估计模型的参数［7］，这样也可以有效避免变量多重相关性的影响。

二、居民生活满意度模型的构建

（一）变量选择与问卷设置

实证分析中研究的对象是浙江省城镇居民（实际研究过程中，主要选取了杭州市、宁波市、温州市、台州市），通过在大中型写字楼、工厂车间、学校、广场、居民区发放居民生活满意度调查问卷表，建立居民生活满意度的结构方程模型，估计模型参数，以此来分析和评价居民生活满意度的影响因素。此次研究共收集问卷354份，通过有效性筛选，确定可用的问卷308份。问卷题目和答案的设置笔者借鉴了5级Likert scale的方法，也就是最低分（非常不满意）是1分，依次是2分、3分，4分，最高分（非常满意）是5分。

问卷中的问题设置了两部分，一部分是以3个外生潜变量ξ1，ξ2，ξ3（分别是身体、社会活动、物质条件）为基础，另外一部分是以3个内生潜变量η1，η2，η3（分别是生活状况、情绪和心理感觉、家庭外部关系）为基础。其中影响身体状况ξ1的变量有身体活动能力X1和身体健康状况X2，这里的X1，X2都不是可以直接观察的变量，需要通过更细地划分可观察变量X11，X12，X13，X14，X15；X21，X22，其他的各变量按照同样的原理设置指标层。调查的问卷中所涉及到的都是可观察变量Xij，Yij。

（二）模型路径图以及观察变量值的计算

首先根据设置的潜在变量与可观察变量建立了图1所示的结构方程模型路径图。

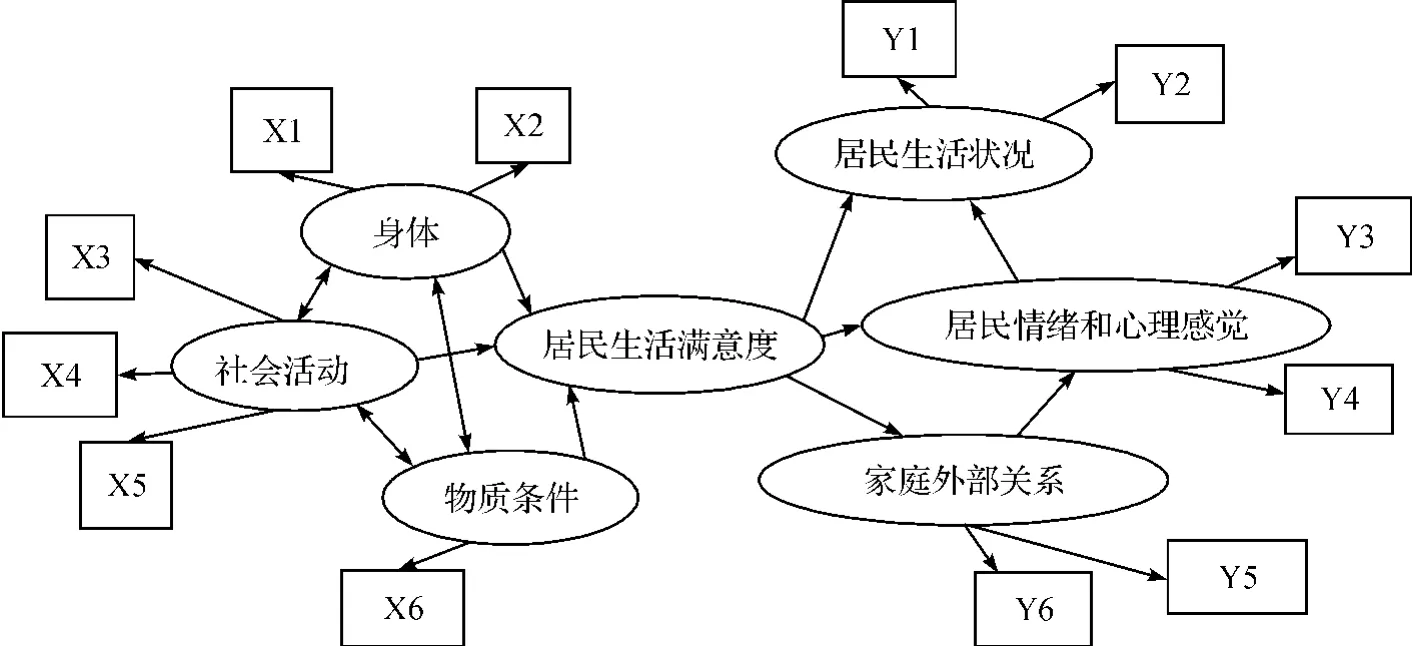
图1 居民生活满意度结构方程模型路径图

图1中椭圆代表潜变量，矩形框代表可观察变量，每个潜变量都是由几个可观察变量决定的，同时，潜变量之间也相互作用，最后居民的生活满意度直接关系着居民的心理感觉，关系到居民的生活状况。

因为在问卷调查的数据集中，没有变量X1，…，X6与Y1，…，Y6的值，于是在建立这两组变量之间的模型前，需要先利用各自的下级变量Xij，Yij求得相应的因子得分值，采用的计算工具是SPSS（Statistical Product and Service Solutions）软件中的主成分分析（Principal Component Analysis）功能模块。

以下只列出变量X1的取值计算过程。

X1的下级指标层有5个可观察的变量X11，X12，X13，X14，X15，把问卷中关于这5个变量的取值输入SPSS数据分析区域，分析得到表1结果。

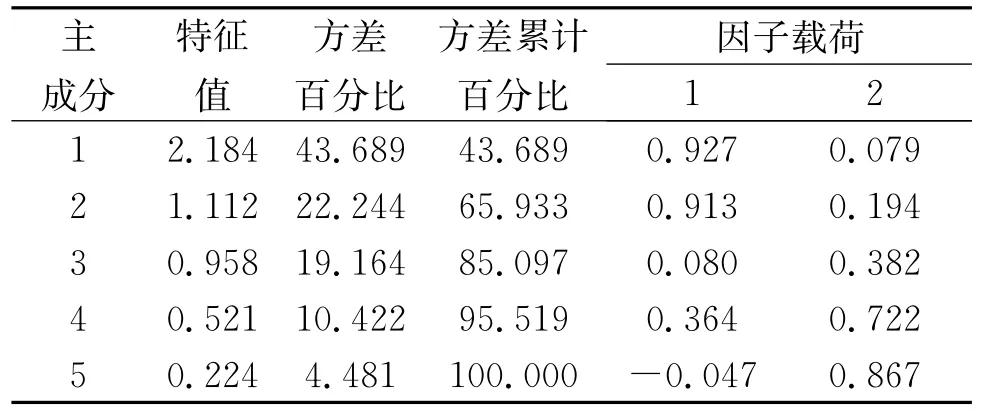
表1 主成分提取与因子载荷

根据主成分对应的特征值大于1的前m个主成分应该提取的原则，结合表1的计算结果，提取2个主成分可以基本反映全部指标的信息，对应的关系式为：

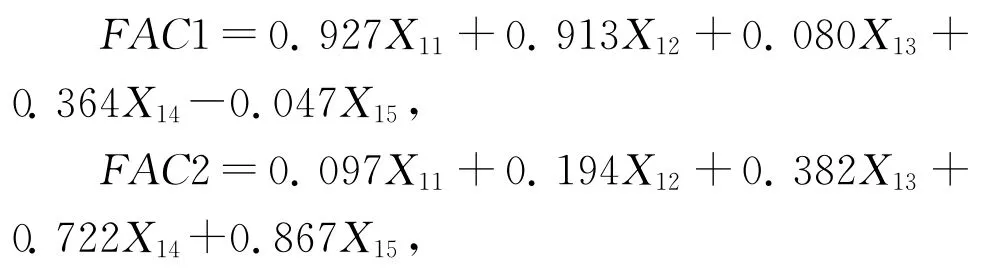
因为最后模型中计算的时候需要的是X1一个变量，所以把上面的两个主成分按照其对应的特征值占总特征值的比重加权算术平均后，作为X1的值。

即：X1＝0．436 89FAC1＋0．222 44FAC2

其他几个变量的取值采用类似的方法计算，于是可以得到X1，…，X6与Y1，…，Y6这12个变量的值。

（三）模型的检验

模型需要通过信度、效度和拟合优度等方面的检验。在SPSS软件相应的功能模块里，可以求得各个潜变量的克朗巴哈α值（Cronbach's Alpha）都大于0．8，整个模型的α值大于0．9，按照这个系数要求的大于0．7的标准，模型都达到了信度的标准。输出的巴特利特球度测试χ2＝238．52，sig＝0．000，说明模型的观察变量和潜变量都具有充分的代表性。

对于拟合优度的检验，可以从表2中的数值分析。

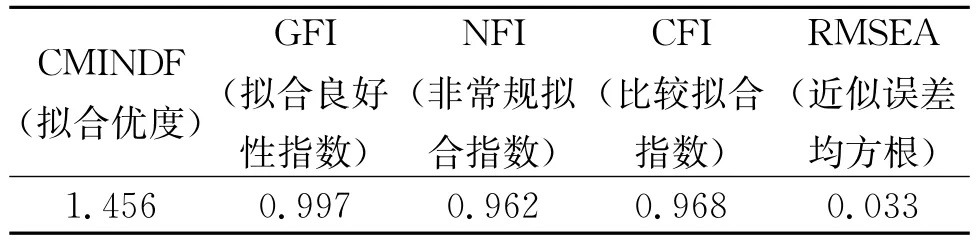
表2 拟合优度检验指标值

一般情况下，拟合优度较好的模型，CMINDF要求小于4，GFI、NFI、CFI大于0．85，RMSEA＜0．1。以上计算结果说明模型拟合程度很好。

三、PLS参数估计

采用PLS方法估计前面建立的结构方程模型参数，需要在Matlab（Matrix and Laboratory）软件里实现。

两个测量模型方程和一个结构模型方程的基本形式如下：

此处载荷矩阵的元素可以直接比较大小，而没有规定有个别元素为1。

根据PLS的原理，需要分别在外生变量和内生变量中按照贡献率最大的原则提取的第一主成分，分别用T1和U1表示，则

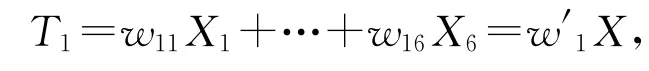
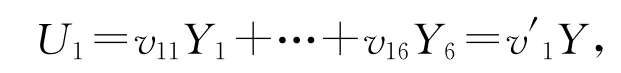
PLS估计的思想就是要使得T1和U1之间的相关程度达到最大，也就是要使得）达到最大，通过拉格朗日乘数法求条件极值的原理，结合样本的数据可以求得以上两个方程的系数向量w′1，v′1，根据测量方程的形式，各个潜变量分别可以写成对应的观察变量的线性组合形式，则求得6个潜变量的值［8－9］。

求得测量方程的估计结果为：

四、结 论

从方程（4）的估计结果可以看出，目前对于居民生活满意度影响较为显著的是其自身身体活动的能力（X1）与居住环境的安全性（X4和X5），相比较而言，物质条件的好坏影响不是特别大，这也充分验证了人们常说的“金钱不是万能的，金钱买不来幸福”，看来有个好身体是生活满意的基础。由方程（5）的估计结果可以看出，就潜在变量中居民的生活状况而言，家庭内部状况（Y1）的影响力稍大于工作状况（Y2）的影响力，很显然，家庭内部婚姻美满、夫妻关系和睦的人更能感觉到生活的幸福和满意，而居民生活态度积极与否、对未来是否充满信心（Y4）也是影响生活满意度的一个重要因素，主观上很自信、对未来充满希望、感觉没有压力的人更能体会到生活中较高的满意度。这也告诉我们，家庭是工作的后盾，情绪是人生的支撑，我们每个人都要热爱家庭、热爱家人，积极参加工作，不断学习充实自己，乐观向上，就能够提高生活的满意度指数。对于居民生活满意度的评价，结构方程模型是一种有效的方法，利用偏最小二乘法去估计模型中的参数也是合理有效的。

［1］廖卫红，孙晓强．移动互联网上消费者购物意向的SEM模型［J］．现代商贸工业，2012（2）：271－273．

［2］邓宏亮．新建地方本科高校教育服务质量与学生满意度的结构方程模型分析［J］．宜春学院学报，2012（9）：119－124．

［3］阿伦·杜卡（Alan Dutka）．美国市场营销学会顾客满意度手册：研究、计划和实施指导［M］．吕一林，阎鸿雁，译．北京：中国宇航出版社，1998：32－64．

［4］Shin D C，Johnson D M．Avowed happiness as an overall assessment of the quality of life［M］．Beijing：Social Indicators Research，1978：379－496．

［5］Krause N．Stressful events and life satisfaction among elderly men and women［J］．Journal of Gerontology，1991，46（2）：84－92．

［6］吴明隆．结构方程模型：AMOS的操作与应用［M］．重庆：重庆大学出版社，2009：10－96．

［7］梁 燕．顾客满意度模型参数估计方法的选择［J］．统计与决策，2007（9）：14－18．

［8］王惠文．偏最小二乘回归方法及其应用［M］．北京：国防工业出版社，1999：26－130．

［9］黄永春，郑江淮，任志成，等．企业自主知识产权名牌的生成机制研究：基于PLS—SEM模型的实证分析［J］．科学学与科学技术管理，2012（4）：156－165．

（责任编辑：许惠儿）

Evaluation Model of Residents'Life Satisfaction and Parameter Estimation

ZHANG Zhi－ying
（School of Sciences，Zhejiang Sci－Tech University，Hangzhou 310018，China）

Residents'life satisfaction is one of the important contents of social and psychological researches．The establishment，inspection and parameter estimation of satisfaction evaluation model are a difficulty and emphasis．The research establishes a measurement model of urban residents'life satisfaction based on structural equation model theory，obtains sample data through questionnaire survey and estimates model parameters with partial least squares．The research shows that，among relevant factors of residents'life satisfaction，residents'body movement ability and the safety of living environment have more significant influence，material conditions do not have great influence，internal family situation has greater influence on life satisfaction than working condition，residents'life attitude and confidence about the future are important factors influencing life satisfaction．

residents'life satisfaction；structural equation model；partial least squares；questionnaire survey；parameter estimation

1673－3851（2014）02－0062－04

C913

A

2013－05－30

国家自然科学基金资助项目（11171308）

张志英（1976－），女，内蒙古呼和浩特人，讲师，主要从事数理统计的研究与教学。