受限支付的强ε-核心博弈理论研究
2014-09-18杨婷
杨 婷
(西安财经学院,陕西 西安 710000)
一、引言
博弈论作为描述现实世界中包含矛盾、冲突、对抗、合作诸因素的理论和方法,在管理、经济、军事等各个学科领域都得到了迅猛的发展和应用。合作博弈作为博弈论的一个重要分支,主要考虑如何分配的问题。合作博弈理论研究的中心问题是研究博弈的各种解,也就是研究如何将合作的收益公平合理地分配给每个合作的参与者。Shapley、Aumann、Maschler、Schimeidler等提出了一系列合作博弈的解,如Shapley值、核心、稳定集、谈判集等,建立和完善了合作博弈的值理论。
Gillies引进了被称之为核心的一个解概念,一个博弈的核心包含这样的支付向量,每个联盟成员的收益和应不少于联盟的收益。核心是研究最多的解概念之一,但在很多情况下,核心也是空的。在此基础上,Shapley和Shubik提出了强ε-核心。
二、具有受限支付的合作博弈
定义2.1:具有特征函数形式的n人合作博弈是一个有序对(N,υ),其中N={1,2,……,n}是参与者的集合,任何的非空子集称为一个联盟,υ是一个定义在N的子集上的,满足υ(φ)=0的实值函数(称为特征函数)。
定义2.2:博弈(N,υ)的分配的定义为一个向量x=(x1,x2,…,xn),满足(i)Σi∈Nxi=υ(N),(ii)x1≥υ({i})对所有i∈N都成立。
定义2.3:博弈(N,υ)的预分配的定义为一个向量x=(x1,x2,…,xn),满足:
Σi∈Nxi=υ(N)
在预分配中,保留了分配中的群体合理条件,而舍去了个体合理条件。
定义2.4:n人合作博弈(N,υ)是超可加,如果对N的所有子集S,T都有υ(S∪T)≥υ(s)+υ(T)。
定义2.5:n人合作博弈(N,υ)是单调的,如果对满足S⊆T的N的所有子集S,T都有υ(s)≤υ(T)。
注:如果(N,υ)是非负超可加博弈,则(N,υ)是单调的。
定义 2.6:令 0 (i)Σi∈Nxi=rυ(N),(ii)xi≥ciυ({i})对所有 i∈N都成立。 注意:r=max{ci:i∈N}对定义2.5中两个条件的一致性是必要的。 定义 2.7:令0 定义 2.8:令 c=(c1,c2,…,cn),0 (i)xi>yi对所有i∈S成立, (ii)Σi∈Sxi+|S|ε≤max{ci:i∈N}V(S)。 定义 2.9:给定c=(c1,c2,…,cn),0 定理2.10:非负超可加博弈(N,υ)的广义强ε-核心,是满足下面两个条件的n维向量x=(x1,x2,…,xn)的集合: (i)Σi∈Nxi=rυ(N),(ii)Σi∈Sxi+|S|ε≥max{ci:i∈N}υ(S)对所有 S⊆T都成立。 证:当 S={i}时,条件(ii)退化为 xi+ε≥ciυ(S),假定 x满足条件(i)和条件(ii),并且对所有的 i∈S,满足 yi>xi,那么: 这意味着y优超x是不可能的,因此x∈C*ε(υ)。 反之,假定x是一个不同时满足条件(i)和条件(ii)的n维向量。如果x不满足条件(i),那么x不是一个广义预分配,因此x∉C*ε(υ)。如果x不满足条件(ii),这意味着对某个非空S⊆T,则: 令: 则α>0,令: 令: 显然有:当i∈S时,yi>0;而当i∉S时,由于: 那么y是一个广义分配。 很明显, 所以 y>x,意味着 x∉C*ε(υ)。 则yi不是一个广义核心。 定理 3.1:若 ε1>ε2,则有 定义3.2:n人合作博弈 (N,υ),ε0是使得广义强ε-核心C*ε(υ)≠φ 的最小 ε,称为博弈的最小广义核心,记为LC*。 显然,若取r=1,ε=0时,广义最小强ε-核心就是通常意义下的核心,即LC*=C(υ)。 定理 3.3:令 0 Minimizez=ε Subject toΣi∈Nxi=rυ(N), Σi∈Sxi+|S|ε≥max{ci:i∈N}υ(S) 该线性规划的解ε*,即为所求最小ε*核心对ε要求,而其余解x*=(x1*,x2*,…xn*)则是最小ε-核心在C*ε(υ)中所含的分配方案。 证:很显然,如果 x∈C*ε(υ),由定理2.10,则x满足上述线性规划条件。 反之,假定线性规划在x*=(x1*,x2*,…xn*)处取得最小值ε*,其包含在 C*ε(υ)所含的分配方案,使得 C*ε(υ)≠φ,证毕。 例3.4:设有一个三人博弈(N,υ),其中N={1,2,3},特征函数的取值如下:很明显,该博弈是非负超可加的,且其核心是空集。这是因为核心的分配必须满足: x1≥0,x2≥0,x3≥0 x1+x2+x3=1, 由后面的三个不等式得: 与x1+x2+x3=1矛盾,所以核心是空集。 此时,强ε-核心非空。 此时,广义强ε-核心非空。 广义强ε-核心是对强ε-核心的进一步扩展,是对核心研究内容和方法的丰富。在广义分配概念的基础上,本文推广了传统合作博弈核心的概念,得到了广义强ε-核心,并且对广义核心建立了类似于已有的一些关于核心的基本结果。 [1]Neumann von J,Morgenstern O.Theory of Games and Economic Behavior.Princeton:Princeton University Press,1944. [2]Gillies D B.Some Theorems on n-person Games.Ph.D Thesis,Princetn:Princeton University Press,1953. [3]Owen G.Game Theory.New York:Academic Press,1955. [4]刘小冬,刘九强,胡健.具有受限支付的合作博弈研究,应用数学学报,2012.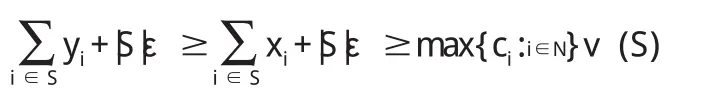
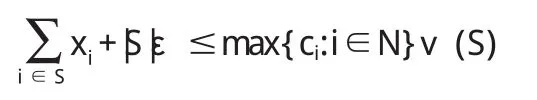
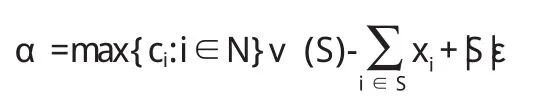
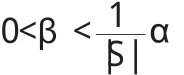
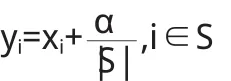

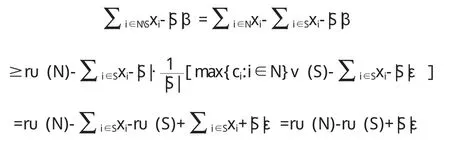

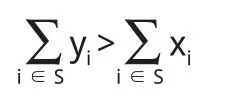
三、广义强ε-核心的性质

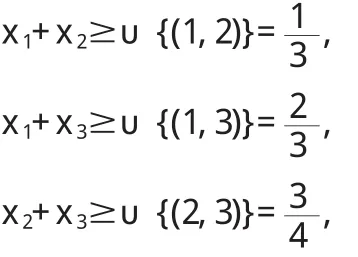
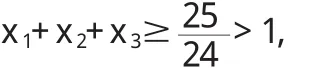


四、结语
