一种线性分组码参数的盲识别方法

2014-09-18王兰勋佟婧丽孟祥雅

电视技术 2014年9期

王兰勋，佟婧丽，孟祥雅

(河北大学电子信息工程学院，河北保定 071002)

在实际数字通信信道中，为了抗击噪声的影响，提高数据传输可靠性，需要进行信道编码技术，即在信息序列中增加冗余码元，使接收序列具有纠检错能力。对信息截获方而言，如何根据接收的序列盲识别出信道编码体制和参数是当前编码研究领域中一个崭新的研究课题，具有重要的现实意义和应用价值［1－2］。

目前，根据公开发表文献知，大部分信道编码识别的研究主要集中在卷积码的盲识别上，针对线性分组码盲识别研究的文献相对较少。文献［3］根据码重分布距离公式估计二进制线性分组码的码长，通过矩阵化简得到生成矩阵，在低误码率下识别效果较好。文献［4］提出了码重分布信息熵算法识别线性分组码码长，适用于较高误码环境，但没有考虑截获序列非同步的情况。文献［5］提出了利用比特频率检测法识别码长和起始点，更适合于较低误码率的环境且所用数据量较大。文献［6］提出了利用汉明距离识别码长和起始点，所需数据量较少，但适应于误码率较低的线性分组码。文献［7］提出了一种基于统计显著水平的快速识别法，首次解决了BCH缩短码的识别问题。文献［8］提出一种利用欧几里得算法识别最大公因式的方法，该方法无繁琐计算。文献［7－8］只针对BCH码而言，针对性较强。文献［9］提出一种通过解调输出的软判决序列来求解含错方程的方法，所需数据量较大。

上述算法或者是数据量较大、针对性较强，不能识别同步点，或者是在低误码条件下才能达到较好的识别效果。针对以上方法的不足，本文提出码重相似度算法识别码长和同步点(本文码字起始点简称同步点)。在此基础上，通过计算码字深度值，选取非零不同深度值对应的码字摆成矩阵形式，即为生成矩阵。最后对码重相似度识别方法进行仿真分析，并讨论该方法的容错性，与其他方法进行了比较，仿真结果表明文中方法在较高误码率为0.01条件下能够有效识别中短码，容错性较好，且所需数据量较少。

1 线性分组码的相关定义及其描述

定义1:(n，k)线性分组码是GF(q)上的n维线性空间中的k维子空间，由qk个码字集合构成，而k个独立向量构成的一组基底完全可以线性表示这qk个码字，将这组基底写成矩阵形式，即为生成矩阵G，G表示形式不唯一，但都是k行n列矩阵［10］。若G有如下形式:G=［Ik，P］，称G为典型生成矩阵。对于循环码，生成多项式的向量形式可由典型生成矩阵的第k行的第k列到第n列表示。本文以二进制线性分组码为例，即q=2。

定义2:一个码字的重量等于该码字中非零元素的个数。对于(n，k)二进制线性分组码，其码字重量为码字中含“1”的个数，也称码重［10］。设qi是 (n，k)分组码中码重为i的码字个数，则重量分布表示为{q0，q1，…，qn}。码重分布概率Pi是重量为i的码字个数在码字总数中出现的概率。

定义3:令c=(b1，b2，…，bn)是二元域上码长为n的线性分组码C的一个码字，定义D(c)=(b2－b1，…，bnbn－1)，称D为c的微分运算［11］。码字c的深度是满足Dz(c)=(0n－z)的最小非负整数z，若这样的z不存在，则c的深度为n。其中Dz(c)表示对c进行z次微分运算。记Dj以j为深度的码字个数，集合 {D0，D1，…，Dn}称为码c的深度分布。下标集{j|1＜j＜n，Dj≠0}称为码c的深度谱。

定理:有限域GF(q)上，任意一个(n，k)线性码c的深度谱中都有且仅有k个非零值，深度互不相同的任意多个码字向量是线性无关的［11］。

2 码重相似度盲识别方法

线性分组码码字之间存在较强的线性约束关系，相比于随机序列，并不是所有任意组合的码字都会出现，导致码重分布不平衡，其码重分布概率与随机序列的码重分布概率之间差异很大，低码率分组码的这种差异程度更明显，因此本文主要针对低码率线性分组码进行识别。将两序列的码重分布概率看成两个向量，采用向量间的相似度衡量两个码重分布概率之间的差异程度。本文根据随机序列与实际序列码重分布概率间差异最大这一特性，提出一种基于码重相似度识别线性分组码码长和同步点的方法。

在统计学中，积矩相关ρW1W2的平方称为判定系数R，用判定系数来衡量实际与随机序列分布的相似度，则W1与W2的相似度表达式为

式中:COV(W1，W2)表示W1与W2的协方差;D(W1)与D(W2)分别为W1与W2的方差，即

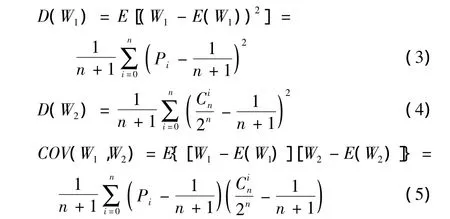
将式(3)～(5)带入式(2)，将式(2)结果带入式(1)得判定系数即相似度

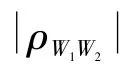
同步点已知，识别码长步骤如下:

1)初始化实际接收序列的码长n。

2)接收序列按码长n分为M个码字。n的变化范围设为1～S，S为最大可能的值。S的选取要根据实际应用需求综合考虑。

4)利用式(6)求R。判断R值是否最小，若最小，则识别码长或码长整数倍，当首次出现谷值时对应码长为真实码长;否则，n=n+1，转到步骤2)，以此循环，直到R最小为止。

码长已知，识别同步点步骤如下:

1)初始化接收序列的同步点m，从任意m位开始，以确定的码长n划分为M个码字。

2)同识别码长步骤3)。

3)利用式(6)求R。判断R值是否最小，若最小，则识别同步点，否则，m=m+1，转到步骤1)，以此循环，直到R最小为止，m的变化范围是1～n+1。

3 深度分布性质识别生成矩阵

用上述方法识别出码长或同步点后，利用线性分组码的深度分布特性识别G。由定义1知，只需找到k个不相关的向量组成矩阵形式，即为G。由定理知，深度值互不相同的非零码字向量作为行向量生成的矩阵是G，根据此结论识别G。将G进行初等行变换，得到典型生成矩阵。对于循环码，进而得到生成多项式。

该方法关键点是识别k值。(n，k)线性码深度谱中有且仅有k个非零值，当已知码长和同步点后，求出M个码字中每个码字的深度值，记为j，j∈{0，1，…，n}，将深度为j的码字个数相加，结果为Dj，则深度分布为{D0，D1，…，Dn}，深度谱为{j|1＜j＜n，Dj≠0}，由定理知选出深度谱中所有不同深度值分别对应的任意一个码字，摆成矩阵形式，即为G。此方法简单，过程易于实现。

4 仿真验证及分析

4.1 已知同步点识别码长

当 BSC 信道无误码时，采用(6，3)，(15，5)，(31，11)，(63，18)，(127，50)5 种线性分组码进行实验，用 MATLAB产生一段随机序列进行编码。取10 000个码元进行仿真，结果如图1所示。

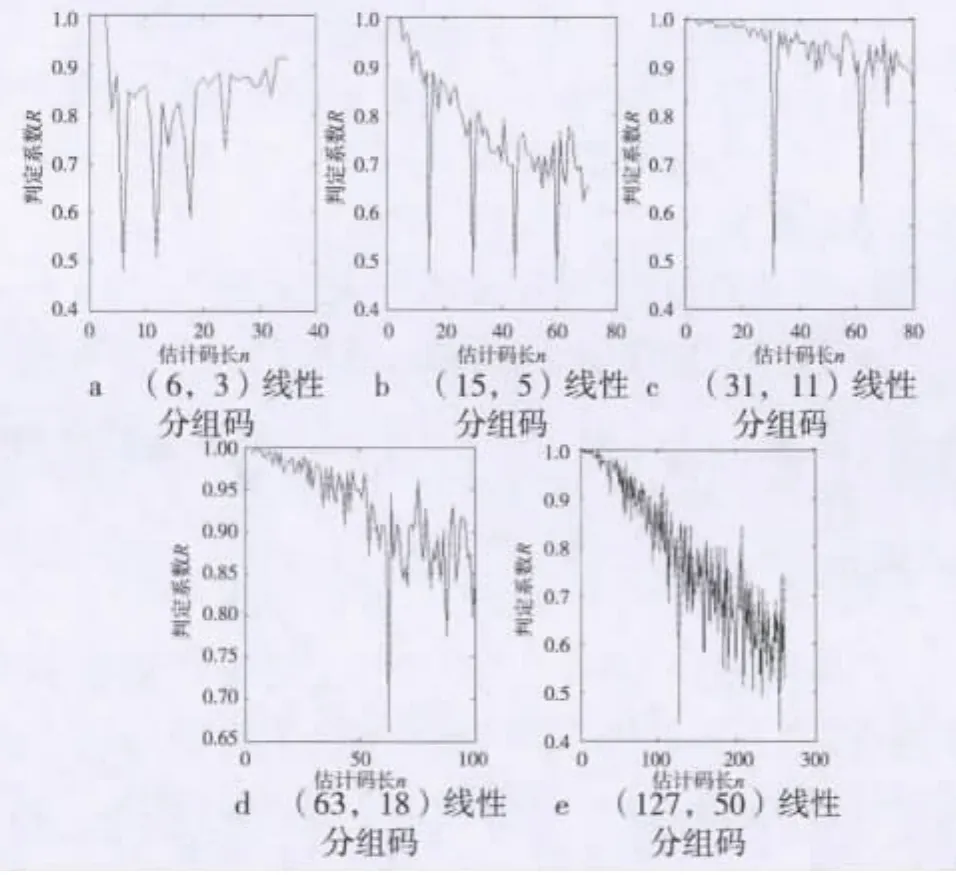
图1 5种低码率线性分组码的码长识别

经图1仿真分析，当遍历的码长是真实码长或码长整数倍时，码组内有完整的线性约束关系，不同码重的码字分布是非等概的，与随机序列码重分布相差最大，相似度最小，即判定系数最小，此时，相似度相对于临近点其值变化较大，因此当首次出现低谷时对应的码长为真实码长。当遍历的码长不是真实码长或码长整数倍时，码组内不具有完整的线性约束关系，不同码重的码字分布趋于等概率，接近随机序列码重分布，此时实际序列与随机序列相似度较高。经仿真分析该方法能正确识别码长n。

当BSC信道有误码时，以(15，5)线性分组码为实验对象，码元个数为10 000个，误码率分别为Pe=0.001，0.01，0.05，0.08，仿真结果如图2 所示。

图2 不同误码率对应的仿真图

从图2可知，码重相似度识别算法受误码率的影响。常规误码率为0.001～0.01，在常规误码率下可以正确识别码长，之后随着误码率的增加，在正确码长或码长整数倍处判定系数变化相对缓慢，在码长整数倍处可能不会出现谷值，当误码率增大到一定程度，出现失真，不能识别码长。如在Pe=0.08时正确识别率很低，由给出的仿真图勉强识别码长。

4.2 已知码长识别同步点

设BSC信道有误码，以误码率为Pe=0.03的(6，3)，(15，5)，(31，11)和Pe=0.01 的(63，18)4 种线性分组码为实验对象，码元个数为10 000个，在码长n已知条件下，从任意起点开始，顺序遍历n个点，在各点处均以码长n划分序列，并统计判定系数，寻找判定系数为最小值时对应的点，即为同步点。用MATLAB进行仿真，结果如图3所示。

图3 码字同步点识别仿真图

计算同步点由m=1遍历到m=n+1对应的判定系数，并作分析，其中m=1表示起点，没有移位，m=n+1表示从起点向右移n位，由于码长为n，所以m=1与m=n+2对应的判定系数是一样的，因此仅比较起点和移位n个起点即可。由图3可知，m分别为5，11，17，22处判定系数最小，即码重相似度最低，码字内线性约束关系最强，此时对应的m值为同步点;而在其他位置，随机性比较强，与随机序列相似度较高。因此在误码率较高的条件下，运用码重相似度方法也能准确识别码字同步点。

4.3 深度分布性质识别生成矩阵

假设截获序列已知码长和同步点，以(15，5)二进制线性分组码为例，取200个码字。计算每个码字的深度值，统计深度值相同的码字个数。通过MATLAB编程，产生深度分布直方图如图4所示，图4中横坐标为深度值j，纵坐标为深度值相同的码字个数之和Dj。

图4对应的深度分布为{4 10 0 0 0 0 0 0 0 0 0 0 10 22 57 97}，深度谱为{1，12，13，14，15}，根据定理知，此线性码k=5即生成矩阵有5行，从这k个非零不同深度值对应的码字中，各取一个码字，组成5×15的矩阵形式，即为生成矩阵，对其初等行变换得到典型生成矩阵。任取k=1对应码字为(111111111111111)，k=12对应码字为(101011001000111)，k=13对应码字为(100110111000010)，k=14对应码字为(111010110010001)，k=15对应码字为(111000010100110)，将此组成的矩阵形式如图5所示。

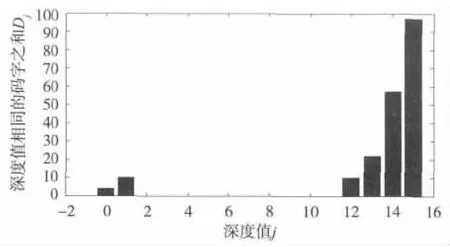
图4 (15，5)线性分组码深度分布仿真图

图5 矩阵形式

从图5可知，G3为典型生成矩阵。本节实验对象(15，5)也属于循环码，G3最后一行为生成多项式的系数，即循环码的生成多项式为g(x)=x10+x8+x5+x4+x2+x+1。利用深度分布识别生成矩阵的方法简单，过程易于实现。

5 容错性能比较分析

根据上述分析，码重相似度识别码长和同步点方法是有效的。下面以(7，4)，(15，5)，(31，16)，(63，16)这 4种线性分组码为实验对象，分别对识别码长和同步点两种情况进行容错性分析。

针对本文和文献［5］两种识别同步点的方法在相同环境下比较分析，对1 000个码字在不同误码率下进行1 000次蒙特卡洛仿真实验，各种线性码的识别率与误码率曲线如图6、图7所示:图6为码重相似度识别同步点的仿真图，明显看出，当误码率为0.18 时，(7，4)，(15，5)分组码的同步点识别率超过了90%;误码率为0.06时，(31，16)分组码的同步点识别率高达90%;误码率为0.016时，(63，16)识别率超过90%;因此本文算法能在高误码率下识别同步点。图7为比特频率检测法识别同步点，其容错性较好，但本文算法相对于比特频率检测法容错性更有优势。

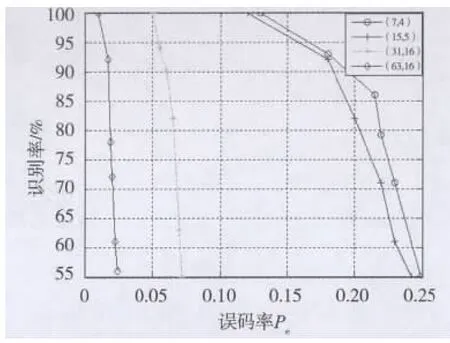
图6 码重相似度算法识别码字同步点

图7 比特频率检测方法识别码字同步点

根据文献［4］知码重信息熵算法容错性强于码重分布距离［3］算法，在此仅对文献［4－5］和本文提出的识别码长算法进行比较。分别取1 000个4种长度的线性分组码码字为实验对象，进行仿真，图8为各种算法的误码适应能力［13］曲线图，图中的误码适应能力是以正确识别率90%以上为门限，不难看出，本文算法与以往算法相比，误码适应能力有一定的提升，在适应误码率1%以上识别码长的正确率高达90%以上，容错性较好。

图8 不同算法误码适应能力

6 结论

根据线性分组码码重分布不平衡与随机序列差异较大的特性，提出了一种码重相似度算法识别码长和同步点。在此基础上，利用深度分布特性，识别生成矩阵，利用高斯消去法产生典型生成矩阵，针对循环码，识别生成多项式，实现了线性分组码的盲识别。最后在不同误码率下对低码率线性分组码进行大量仿真实验，并与其他算法进行对比，码重相似度识别算法能在误码率为0.01情况下识别低码率线性分组码码长和同步点，具有较好的容错性，此方法的误码适应能力也有一定的提高。利用深度分布特性识别出生成矩阵，此方法简单，随着码长增加数据量不断扩大，此识别生成矩阵的方法对无误码情况下的中短码及低码率的线性分组码识别效果较好。运用深度分布特性识别高误码率下、高码率的线性分组码参数成为下一步研究的重点。

［1］解辉，黄知涛，王丰华.信道编码盲识别技术研究进展［J］.电子学报，2013，41(6):1166－1176.

［2］王伟祥，刘玉君.基于信道编码的信息隐藏技术研究［J］.电视技术，2006，30(3):284－286.

［3］昝俊军，李艳斌.低码率二进制线性分组码的盲识别［J］.无线电工程，2009，39(1):19－24.

［4］陈金杰，杨俊安.基于码重信息熵低码率线性分组码的盲识别［J］.电路与系统学报，2012，17(1):41－47.

［5］陈金杰，杨俊安.一种对线性分组码编码参数的盲识别方法［J］.电路与系统学报，2013，18(2):248－254.

［6］闫郁翰，汤建龙.基于汉明码距离的二进制线性分组码盲识别方法［J］.通信对抗，2011(4):20－23.

［7］张永光，郑仕链.BCH码的参数识别研究［J］.西安电子科技大学学报，2013，40(5):92－98.

［8］王兰勋，李丹芳，汪洋.二进制本原BCH码的参数盲识别［J］.河北大学学报，2012，32(4):416－420.

［9］于沛东，李静，彭华.一种利用软判决的信道编码识别新算法［J］.电子学报，2013(2):301－306.

［10］王新梅，肖国镇.纠错码——原理与方法［M］.修订版.西安:西安电子科技大学出版社，2001.

［11］李超，耿晋.有限域上线性码的深度分布［D］.长沙:国防科学技术大学，2006.

［12］王磊，胡以华，王勇，等.基于码重分布的系统循环码识别方法［J］.计算机工程与应用，2012，48(7):150－153.