基于环状库特流的管柱下井压力分析

王言聿，成志强，柳葆生

(西南交通大学力学与工程学院，成都 610031)

油管传输射孔工艺(TCP)是石油工业中广泛应用的技术。油管传输射孔工艺是利用油管(钻杆)连接射孔枪，送至油层部位射孔，以打开油气层的一种采油工艺。其最大优点是可在大负压条件下射孔，易于解除射孔对油层的伤害，且一次射孔层段的厚度较大。在TCP工艺中，射孔弹的引爆方式包括井口管柱内投棒引爆、管柱加压引爆、环空加压引爆和压差式引爆等。由于大部分引爆方式均与井液作用于点火头上的压力相关，因此了解管柱下放过程中点火头的压力尤为重要。在下放过程中，套管内井液的静压与动压组成管柱外表面承受的总压。其中静压仅与下放深度相关，而行业内习惯称为“波动压力”的动压，其计算必须考虑井液流动的情况。目前在TCP作业中，对“波动压力”作用没有进行精确计算，存在起爆装置未到达目的层提前发射的危险。

南堡油田的误射事故便是由于在下放工艺中忽略了“波动压力”，导致射孔枪的销钉未到预定位置便被剪断而提前射孔。李贵吉等［1］对此事故进行了分析，指出波动压力与下放速度相关，提出了管柱结构尺寸的最低要求。但是文献［1］中采用指数公式确定井液返流的速度分布，动压的推导并未基于流体力学最基本的质量守恒定律，结果可能不够准确。计算流体力学(CFD)的发展虽然提供了定量分析流动参数的可能，但由于套管中的环状流体域具有长径比极大的特点，造成网格划分困难、计算量大，在现有计算机条件下不适于工业应用。本文基于牛顿层流下的库特流理论，分析管柱下放速度对压力的影响，推导了波动压力随管柱下放速度的解析公式，并编程实现了多级管柱的动压叠加效应的计算，计算结果可为管柱设计和下放工艺提供参考。

1 管柱下放的流体力学模型

为了建立管柱下放过程的力学模型，引入一些假设是必要的。如图1所示，套管可简化为一竖直的圆柱体空间，其中含有一定量的液体，称为井液。井口与大气相连通，井液与大气间的界面称为“自由液面”。在如图1、2所示的柱坐标系中，其坐标原点位于井口平面，x轴正方向指向井底，假设:①套管的内壁是光滑壁面;②自由液面不得高于井口;③井液是不可压缩的牛顿流体，且其物理性质不随井深变化;④流体域Ω中的流动为缓变流，且其水头损失可忽略不计［3］;⑤ 流体域Ω中的流动为绝热的。

由于管柱下放速度并不高，而井液具有一定密度与黏度，当流场充分发展后，假设④是合理的;生产实践证实了井液流动的热效应并不明显［4］，假设⑤亦是合理的。

典型的管柱结构，如图3所示。管柱由直径长度不同的管段组成，各管段外表面与套管间构成了环形的流体域，记为Ω。如图2所示，a为该管段的直径，b为该管段与套管内壁间的间隙量，则a+b为套管内径。

流体域Ω上的控制方程为一元流的动量守恒［2］。对流体质点 x，∀x∈Ω，有

其中:u是井液的轴向速度，即x方向的流速;μ为井液的动力黏度。

当 r=a 时，u= ¯v;当 r=a+b 时，u=0。其中 ¯v为管柱下放速度。应该指出的是:由于井液自身的重力与其静水压压力的梯度作用平衡，故式(1)中的压力p未考虑静水压的作用。

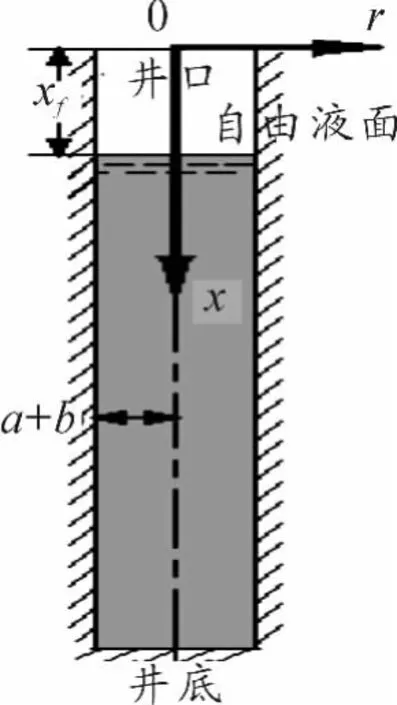
图1 套管空间示意图

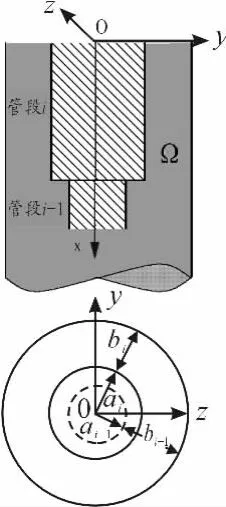
图2 流体域示意图

图3 总装管柱结构示意图

2 井液压力的解析推导

2.1 井液压力的计算

过管柱上任意一点，作一垂直于管柱轴线的平面，记为c。由质量守恒定律可知，在单位时间内c处管柱的入水体积等于通过环面c的井液流量Q:

其中rc为c截面通过的管柱半径。同时，Q又可以用环形域的流速u表示为:

联立式(2)与式(3)，可得出u的表达式。将其代入式(1)的积分形式，有:

令任一时刻t，管柱上一点m的流体波动压力为pm，由式(4)推导可得:

其中:ai为t时刻位于自由液和m点之间各管段的半径;Li为这些管柱对应的长度;Ai与Bi根据式(4)计算。需要注意的是:在式(5)中，m点所在的管段中没入井液中的部分也需计入。

2.2 自由液面位置的修正

记自由液面到坐标原点的距离为xf，如图1所示。管柱底部即点火头Q的下端面亦为一平面，记此平面到原点距离为xk，如图2所示。记t=0时刻的 xk为 xk0，显然 xk=xk0+记 t=0 时刻的自由液面为“初始液面”，此时的xf为xf0，随着管柱浸入井液，自由液面将上升Δx，则xf=xf0+Δx。

选取xf0直至井底的区域为控制体vi，若管柱触水后继续下放，流出控制体 vi的流体总体积vf为

其中:aj为位于初始液面下各管段之半径;Lj为对应管段的长度。需要注意的是:通常存在未完全位于初始液面以下的一级管段，则此时Lj只计入其位于初始液面下的长度。

向上返流的流体均涌入初始液面以上导致自由液面上升，记其上升高度为Δx，则有

式中Lk为初始液面和新自由液面之间各级管柱的长度。同样需要注意的是:对于未完全没入井液的管段，对应的Lk仅计入没入段的长度。

Lk的值可通过联立式(6)和式(8)进行求解。式(8)中:ak为全部或部分位于初始液面与新自由液面之间管段的半径;rk为对应位置的套管直径，一般为常数。

由于自由液面不得高于井口，若按式(7)解出的 Δx大于 xf0，则 Δx=xf0。

3 算例分析

以图2所示的管柱为例，各管段的编号及几何尺寸见表1。假设套管内径为157.3 mm，自由液面距井口的距离为0 m，井液的物理性质与水相同。

表1 管段尺寸

续表

下放速度 ¯v取1.5 m/s，自由液面位于井口，管柱下放深度为1000 m。取各管段的上下端点为“测点”，按式(5)计算的井液压力称为“测点压力”。值得注意的是，这里的“测点压力”是井液流动形成的动压，未包含静水压的作用。

图4 测点波动压力与测点距管柱底端距离关系曲线

图5 下部点火头波动压力与封隔器直径关系曲线

测点压力与测点距管柱底端距离的关系如图4所示。图4中在封隔器处出现了较大的压力梯度，这是由于在封隔器和套管间的环形域存在较高的流速。对于黏性一定的牛顿流体，压力梯度与流速正相关。由大直径管段引起的较大压差将传递到该管段以下的管柱部分，这就会产生所谓的“憋压”效应。憋压效应将极大增加管柱下部各管段的压力，甚至引起点火头提前发火。由式(4)和(5)可见:各管段两端的压力差与管段长度成线性关系，但与管段半径间的关系尚不明确。现将封隔器的直径作为变量，其余管柱尺寸同表1，各项参数同上例。作下部点火头中部的测点压力与封隔器直径的关系曲线，见图5。封隔器直径增大导致的“憋压”与直径大小并非线性关系。随着封隔器直径接近与套管内径，下部点火头的压力呈指数增大，这种趋势增大了憋压现象的危险性。在使用了直径与套管内径大小较为接近的管段，或当套管存在几何变形时，应当限制下放速度以降低风险［5－6］，并对点火头压力进行实时监控，以确保在准确的位置射孔［7－8］。

需要进一步说明的是:式(4)的计算结果只包括了井液流动形成的液体动压，而实际的井液压力还包括静水压的作用。根据静水压计算公式，管柱下放1000 m时，下部点火头处的静水压约为10 MPa。可见，当憋压效应不明显时，静压为下部点火头承受的主要压力;而当管柱直径增大时，井液动压的作用则明显增大;当封隔器半径大于157 mm时，该管段上的动压已占点火头总压的55%以上，在管柱设计时必须避免这种情况发生。

4 结论

1)推导了管柱两端动压与管几何尺寸及下放速度的解析关系式，并编程实现了多级管柱的动压叠加效应。

2)通过算例证实了“憋压”效应的存在，显示出“憋压”压力与管柱直径的关系。

［1］李贵吉，张建民，王承恩.南堡油田NP511井下管柱误射孔事故原因分析［J］.测井技术，2008，32(5):471－475.

［2］庄礼贤.流体力学［M］.合肥:中国科技大学出版社，1991.

［3］Sambo A S.Numerical computation of laminar flows in rotor-stator cavities［C］//IN:Numerical methods in laminar and turbulent flow;Proceedings of the Fourth International Conference.［S.l.］:［s.n.］，1985:274 －286.

［4］刁林涛.直井油管内加压起爆管柱校深技术［J］.石油仪器，2012，26(1):11 －15.

［5］葛莉.特殊井的射孔深度矫正新技术［J］.石油仪器，2009，6(1):23 －27.

［6］梁政，邓雄.高温高压测试管柱力学初探［J］.天然气工业，1998，4(1):17 －21.

［7］曾志军，胡卫东，刘竟成.高温高压深井天然气测试管柱力学分析［J］.天然气工业，2010，30(2):85 －87.

［8］刘达林，李治平，李允.深井气井试油合理测试时间确定方法研究［J］.天然气工业，2002，24(2):15 －17.