基于有限元方法的木材含水率和密度空间分布模型1)

周 正 孙丽萍 姜 滨

(东北林业大学，哈尔滨，150040)

木材干燥处理前，确定木材的初始含水率和初始密度的空间分布，不但能为木材干燥过程中各参数的设定提供参考依据，而且对提高木材干燥质量具有重要意义[1]。木材具有各向异性和非均匀性的特点[2]，大部分计算模型并不能有效地描述木材含水率和木材密度的空间分布。

在工程分析领域，有限元方法是用来解决边界问题近似解的数值处理方法[3]。利用有限元方法分析实际问题时，能否精确对研究对象进行网格划分，会对最终的仿真结果产生很大的影响[4]。影响选择网格类型的主要因素有[5]:研究对象的几何特征(形状、尺寸等)，仿真的精度要求，计算机的配置和对计算时间的要求等。随着人们对有限元法越来越深入的研究，其应用范围越来越广泛[6]，有限元网格的划分方法也越来越多[7]，目前应用较为广泛的方法主要有以下几种:全局正交网格[8]、PEBI网格[9]、角点网格[10]和控制体积有限元网格[11]。根据网格的特点和试验的需要，本文采用控制体积有限元方法对板材模型进行网格划分。建立了木材含水率和密度空间分布的数学模型。

1 数学模型的建立

1.1 有限元网格的生成

试验中，为了减少计算量，只研究板材的四分之一。划分有限元网格时，把板材的立体模拟图划分为若干个三角棱柱体，即:每一个子单元都为空间图形，能够在三维坐标中表达出来。三维有限元网格的建立方法，是在建立二维有限元网格方法的基础上发展起来的，原理:首先在xy平面上建立三角网格，然后在z轴方向将每个三角网格延伸形成空间的三角棱柱体。图1表示在x－y平面上对板材横断面进行了网格划分，共有2045个子单元;图2表示在z轴上对板材径向进行了网格划分，几何比率为1.05;图3是四分之一板材在空间上的网格模型，总共有12270个子单元。

图1 x－y平面上的网格划分

1.2 板材的初始密度分布

试验用板材包括早材与晚材，密度分布在248～1113 kg/m3之间，平均密度为 476.43 kg/m3，木材的纹理角度处于 27.83°～91.40°。根据板材的密度和纹理角度对每个网格进行赋值，为了把密度分散到每个网格的节点上，用体积加权平均算法计算(见式(1))。

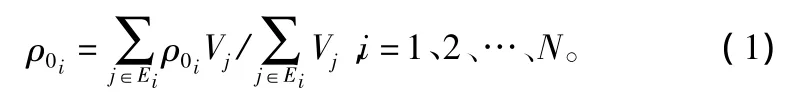
式中:ρ0i是在i点木材密度的计算值;Ei包含了以i点为顶点的子单元;Vj是与节点i相关联的子单元j的体积;N是整体网格的节点数。式(1)中的分母等于节点周围的体积总和，分子等于分母中节点i周围体积的固体质量。

图2 z轴上的网格划分

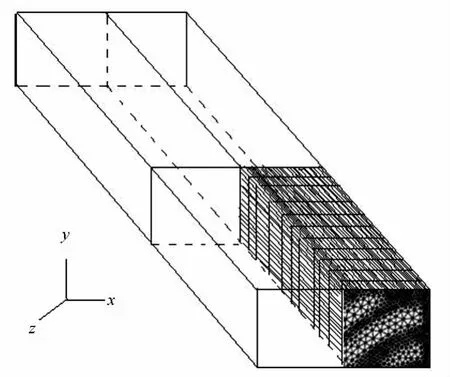
图3 板材的有限元网格模型

1.3 板材的初始含水率分布

由于木材的多孔性，在干燥前板材的温度分布有一定规律，假设板材的最初温度与周围温度相同。板材最初的含水率需要通过一个非线性方程确定，这个非线性方程需要同时满足毛细力的平衡方程和总质量平衡方程。对于一个具有N个节点的有限元网格，N+1阶的非线性方程为:

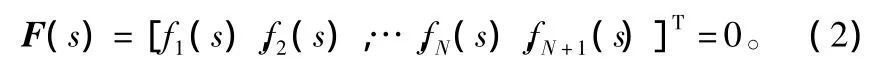
式(2)中的坐标函数为:

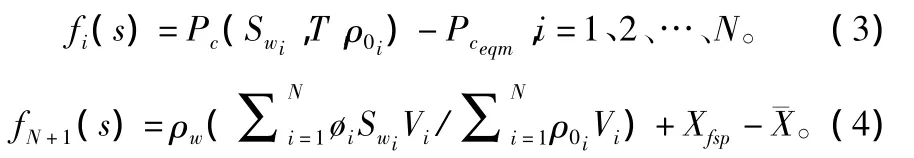
式中:解向量 S=(Sw1，Sw2，…，SwN，Pceqm)T，Swi为节点i处的液体饱和度;Pceqm为平衡毛细管压力;¯X为板材初始平均含水率;Xfsp为板材的纤维饱和点;ø为板材的孔隙率;Vi为节点i的体积。

再利用牛顿法解非线性方程组:

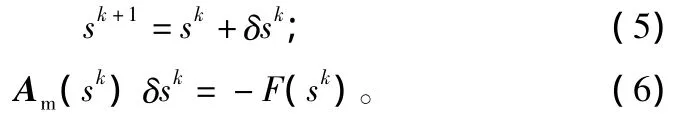
式中:δsk为牛顿修正矢量，Am为雅各比矩阵的近似值。

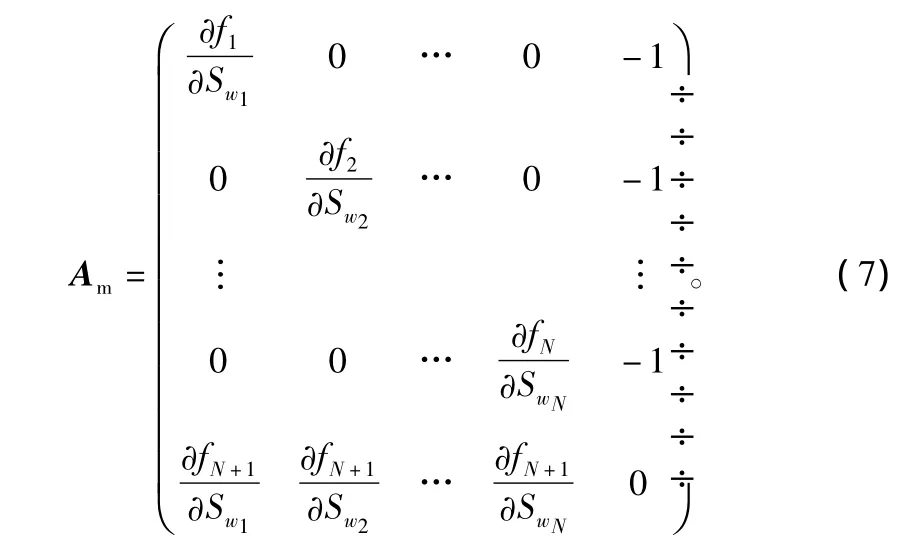
其中，矩阵中的各项能够根据一阶有限差分逼近原理计算出来。未知量的次序保证了系统通过因式分解获得牛顿校正，通常情况下，经过十次迭代就能得到木材初始平均含水率的收敛解，然后通过公式(8)可以求出在每个节点的木材初始含水率。

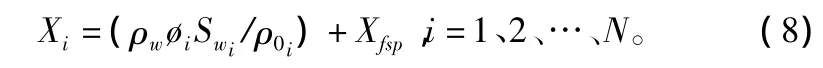
2 仿真结果及分析

根据建立的木材初始密度模型，得到图4所示的板材四分之一的木材密度分布图。在图4中可以明显地看出，不同年轮周围板材密度的变化;仿真图中的深色区域是密度较低的早材，而浅色区域则是密度较高的晚材。

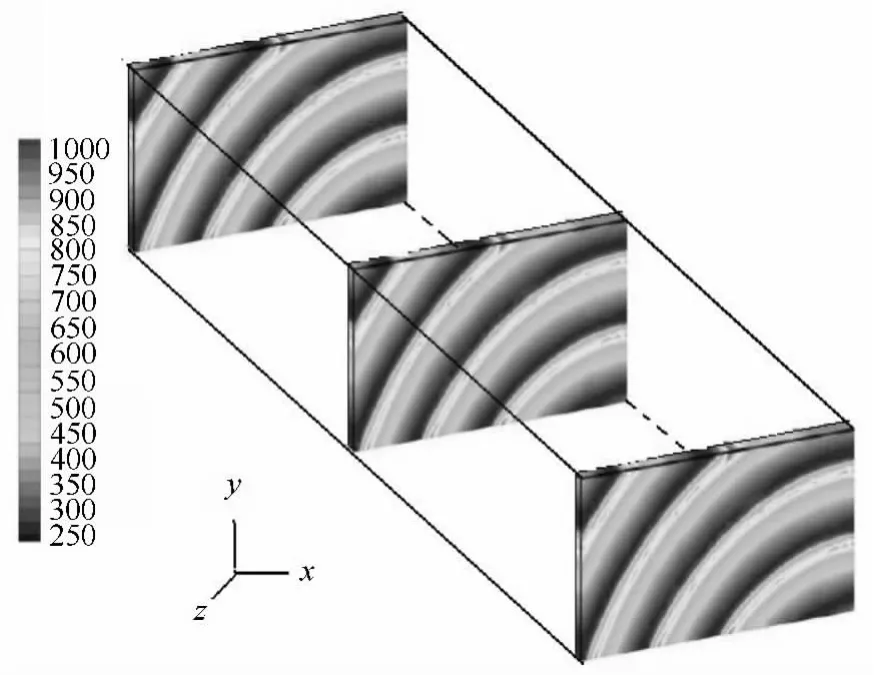
图4 板材的初始密度分布(单位:kg/m3)

根据建立的木材初始含水率的数学模型，得到图5的板材四分之一的木材含水率分布图。板材的初始含水率分布在63.2% ～296.7%之间，从仿真图中可以明显地看到晚材的含水率低于早材的含水率。

图5 板材的初始含水率分布(单位:%)

3 结束语

讨论了利用有限元方法建立木材含水率和密度空间分布模型的必要性、可行性和优势，通过控制体积有限元方法对板材模型进行了网格划分，采用了有限元法将方程离散化，从而建立了木材含水率和密度空间分布的数学模型，最后通过建立三维仿真图验证了模型的准确性。因此，利用有限元方法研究木材含水率和密度的空间分布是一种可行的、较为精确的方法。

[1]孙丽萍.木材含水率在线检测融合体系及仿真技术研究[D].哈尔滨:东北林业大学，2008.

[2]Siau J F.Transport processes in wood[M].Berlin:Springer Cooperation，1984.

[3]鲁建霞，苟慧芳.有限元法的基本思想与发展过程[J].机械管理开发，2009，24(2):74 －75.

[4]郭洪锍.基于ANSYS软件的有限元法网格划分技术浅析[J].科技经济市场，2010(4):20－21.

[5]郑正，雷君相，罗宇舟.基于ANSYS对塑料齿轮的结构静力学分析[J].制造业自动化，2010，32(5):163 －166.

[6]刘英魁.有限元分析的发展趋势[J].中国新技术新产品，2009(6):157.

[7]吕心瑞.基于控制体积方法的离散裂缝网络模型流动模拟研究[D].东营:中国石油大学，2010.

[8]姜瑞忠.数模网格构建与参数网格化技术研究[D].东营:中国石油大学，2008.

[9]王长飞.PEBI网格的生成与应用研究[D].北京:中国社会科学院，2009.

[10]叶继根，吴向红，朱怡翔，等.大规模角点网格计算机辅助油藏模拟历史拟合方法研究[J].石油学报，2007，28(2):83－86.

[11]戴福洪，张博明，杜善义，等.RTM工艺注模过程模拟的有限元/控制体积方法和流动分析网络技术比较[J].复合材料学报，2004，21(2):92－98.