基于非线性度量误差的杉木相容性生物量模型1)

蔡兆炜 孙玉军 施鹏程

(省部共建森林培育与保护教育部重点实验室(北京林业大学)，北京，100083)

森林作为陆地生态系统的主体，是陆地上最大的碳储库和最经济的吸碳器，对维护区域生态环境及全球碳平衡，缓解全球气候变暖发挥着不可替代的作用。森林生物量及其生产力的大小则是评价森林碳循环贡献的基础，也是森林生态功能评价的重要参数，因此，进行森林生物量的监测和评估具有十分重要的意义[1－6]。

林木的生物量涉及干材、干皮、树叶、树枝和树根等分量[7]，林木总生物量应该等于各分项生物量之和。为了满足这一个基本的逻辑关系，在建立地上生物量和各分量生物量方程时，就必须要使各个方程之间具有相容性[8]。骆期邦等[9]研究得到了解决总量和分量之间不相容问题的两种方法，即线性联立模型和非线性联合估计模型。唐守正等[10]对5种非线性联合估计方案进行了对比研究，提出了以树干生物量作为控制量，采用两级联合估计的方法。Parresol[11]提出采用非线性似然无关回归方法，解决非线性生物量方程的可加性问题。Bi H Q等[12]建立了以对数转换为基础的可加性生物量方程系统，并采用似然无关回归方法，对方程参数和偏差校正因子进行联合估计。

一般的回归模型，通常是假定自变量的观测值不含误差，而因变量的观测值含有误差。误差的来源有很多，如:测量误差、抽样误差等，一般统称为度量误差。当自变量和因变量的观测值都含有度量误差时，通常的回归模型估计方法就不再适用，而必须采用度量误差模型方法[13－15]。李永慈等[16]利用非线性度量误差联立方程组，建立了全林整体模型，其效果明显优于最小二乘法。曾伟生等[17]利用度量误差模型方法，建立了贵州省人工杉木相容的立木材积方程和地上生物量方程，进一步验证了度量误差模型的科学性和适用性。

杉木(Cunninghamia lanceolata)人工林是我国南方集体林区栽培历史最悠久、栽培范围最广的重要用材林之一，也是福建省的重要森林类型之一[18]。以福建将乐国有林场的人工杉木为研究对象，应用非线性度量误差模型的方法，建立总量与分量相容的生物量模型，并评价模型精度和适用性。

1 研究区概况

研究区位于福建省西北部的将乐县国有林场，地理坐标为 26°26'～27°04'N，117°05'～117°40'E，地处武夷山脉东南部，以中、低山为主，最高峰陇西山海拔1620 m。属亚热带季风气候，具有海洋性和大陆性气候特点，年平均气温18.7℃，降水量1672.3 mm，无霜期273 d。境内气温较高，夏季时间长，冬天较暖和，霜冻较少，生长期长。将乐县土壤有6个土类15亚类44个土属。境内土类多样，其中红壤水湿条件比较好，是栽培杉木的好土壤。实验区野外调查样地杉木林的林下草本种类共23种，芒萁(Dicranopteris dichotoma)分布最多。杉木林下灌木种类共16种，粗叶榕(Ficus hirta)分布最多。杉木林下更新幼树种类共7种，杉木分布最多[19]。

2 研究方法

2.1 样地设置和调查方法

在全面踏查的基础上，结合立木径级与年龄分布规律，按典型取样原则，设置杉木人工纯林标准地共28块，其面积根据生物多样性和地势的实际情况而定，最小面积为20 m×20 m，最大面积为30 m×30 m。按照顺序为样地编号，记录样地的海拔、坡向、坡度、坡位、森林类型、土壤类型和林分结构。在每个样地内，进行每木检尺，记录胸径、树高、冠幅等特征因子，得出平均胸径和径级分布。按径级记录株数、平均胸径，并依此平均胸径选取1～3株样木，最终保证所选样木按径级均匀分布。

采用分层切割，测定样木地上生物量[20]:称取每1 m区分段树干、枝叶鲜质量，并取圆盘、树皮样品;量测树枝的基径和长度后，选取3～4个标准活枝，分离枝、叶，再称质量并取样。将各器官样品带回，在105℃恒温下烘干，称取样品干物质质量。通过计算各器官的含水率，计算相应干质量。最后，将木材和皮的干质量相加，得到树干干质量;枝和叶的干质量相加，得到树冠的总干质量;树干和树冠的干质量相加，得到全树地上部分的总干质量[21－22]。本文研究的生物量仅限于地上部分。

2.2 建模方法

2.2.1 总量和各分量独立模型

全世界范围内已经建立的生物量(包括总量和各分量)模型超过2300个，涉及的树种在100个以上。立木生物量模型的一般结构形式有以下3种[23]。

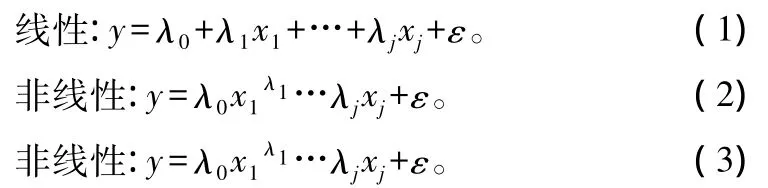
式中:y为立木生物量，xj为胸径、树高、冠幅等变量，λj为模型参数，ε为误差项。模型(2)和(3)的唯一区别是误差项的性质，模型(2)为加性误差，模型(3)为乘积误差。由于生物量数据通常都存在异方差，因此非线性模型一般采用(3)式，并采用加权最小二乘法进行拟合。本文也采用(3)式分别拟合只包含胸径和同时包含胸径、树高的一元、二元生物量方程。

式中:wi为总量或分量生物量，ai、bi、ci为模型参数，i取 0、1、2、3、4，分别代表地上部分、干材、干皮、树枝和树叶;D为胸径;H为树高。

2.2.2 相容性模型

非线性度量误差变量联立方程组(即多元非线性度量误差模型)的向量形式为[24]:

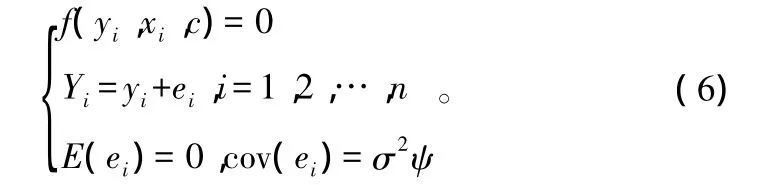
式中:xi是q维无误差变量的观测数据，Yi是p维误差变量的观测数据，f是m维向量函数，yi是Yi的未知真值，误差的协方差矩阵记为Φ=σ2ψ，ψ是ei的误差结构矩阵，σ2为估计误差。

春光这样明媚，花儿万紫千红，这一切居然无人欣赏，没人理会，她伤感了，难道自己就像无人爱惜的春天，悄悄流逝，年华虚度吗？“没乱里春情难遣，蓦地里怀人幽怨”中，杜丽娘做了个梦，在梦中她见到手持柳枝的少年书生，大胆地和他幽会了。《惊梦》之后，家教已锁不住她，她不顾母亲的教训，第二天又去后花园寻梦。

曾伟生等[2]利用非线性度量误差模型方法，根据东北4省落叶松和南方9省马尾松的生物量实测数据，采用总量直接控制和分级联合控制两种方案，拟合相容性生物量模型，结果表明:两种方案都行之有效，且拟合效果差异不大，而从模型的复杂程度考虑，建议采用总量直接控制方案。董利虎等[1]在研究东北林区天然白桦相容性生物量模型时也采用了上述两种方案，拟合结果显示，总量直接控制方案要略优于分级联合控制方案。为了避免分级联合控制产生误差叠加现象，本文采用总量直接控制方案，研建人工杉木的相容性生物量模型。

总量直接控制方案是把地上总生物量直接分成干材、干皮、树枝、树叶4个分项，确保各分量之和等于总量。在构建一元、二元生物量模型时，假设干皮、树枝、树叶分别占总生物量的相对比例函数为f1(x)、f2(x)、f3(x)。即:

式中:ai、bi、ci为参数。设 g0(x)为地上总生物量模型，即g0(x)=w0。则相容性生物量方程系统为:

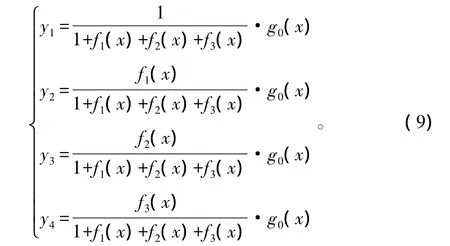
式中:y1、y2、y3、y4分别为干材、干皮、树枝、树叶的生物量，x为林木胸径(D)、树高(H)等因子。选择干材方程的分子为1，是因为干材占全树生物量比重最大且最稳定。建模时，需先根据生物量数据分析确定f1(x)、f2(x)、f3(x)这3个相对比例函数(相对于干材为1的变化函数)的形式，并求出各个参数的估计值。再用这些估计值作为初值，用度量误差模型方法求解模型系统(9)的参数值。

生物量模型普遍存在异方差性，为了解决好这一问题，就要选用合适的权函数进行加权回归估计进行异方差的消除。已有研究常采用的方法是对数回归或加权回归，曾伟生等[17]在研究贵州省人工杉木材积与地上生物量模型时，通过对通用权函数W=1/f(x)2和根据独立拟合方程的方差建立的权函数W=1/g(x)2进行对比分析，发现后者的效果要略好些，而且对源于方差的权函数，按一元、二元回归方程进行对比，发现其差异很小。故本文采用非线性加权回归方法，根据地上生物量独立拟合方程的方差所建立一元回归方程来确定权函数，采取每一个方程两边乘以权重变量G=1/g(D)的方法进行处理。

2.3 模型的评价与检验

对建模样本进行重复抽样，随机抽取30%作为检验样本，计算检验指标，进行模型的综合评价。模型评价与检验的常用指标主要有确定系数(R2)、估计值的标准差(SEE)、总相对误差(TRE)、平均系统误差(MSE)、平均预估误差(MPE)和平均百分标准误差(MPSE)[25]。

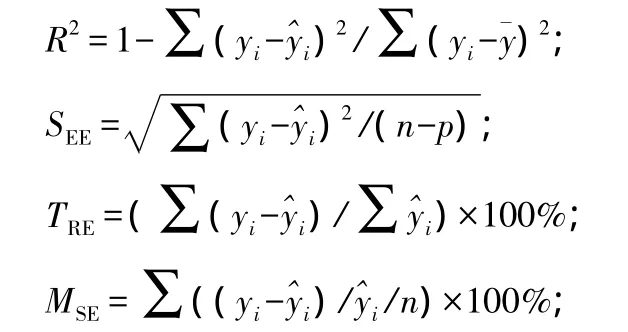
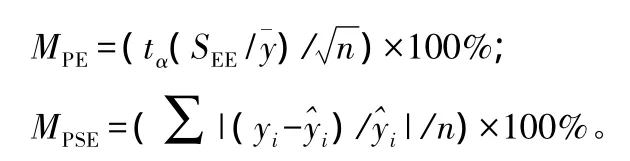
式中:yi和分别为第i株样木的实测值和预估值，为全部样木实测平均值，n为样本总数，p为参数个数，tα为自由度n－p、置信水平为 α 时的 t值(此处取 α=0.05，则 tα=1.98)。

3 结果与分析

表1 杉木样木基本特征因子

表2 杉木样木实测生物量基本情况

3.1 独立模型拟合

人工杉木一元、二元生物量总量与各分量独立方程拟合结果(见表3)。由表3可知，独立建立的地上总量、干材和干皮模型的确定系数(R2)都较高，树枝和树叶的确定系数相对较低，分别为74%和86%，拟合效果较好，拟合精度符合要求，总体上来说二元模型优于一元模型。

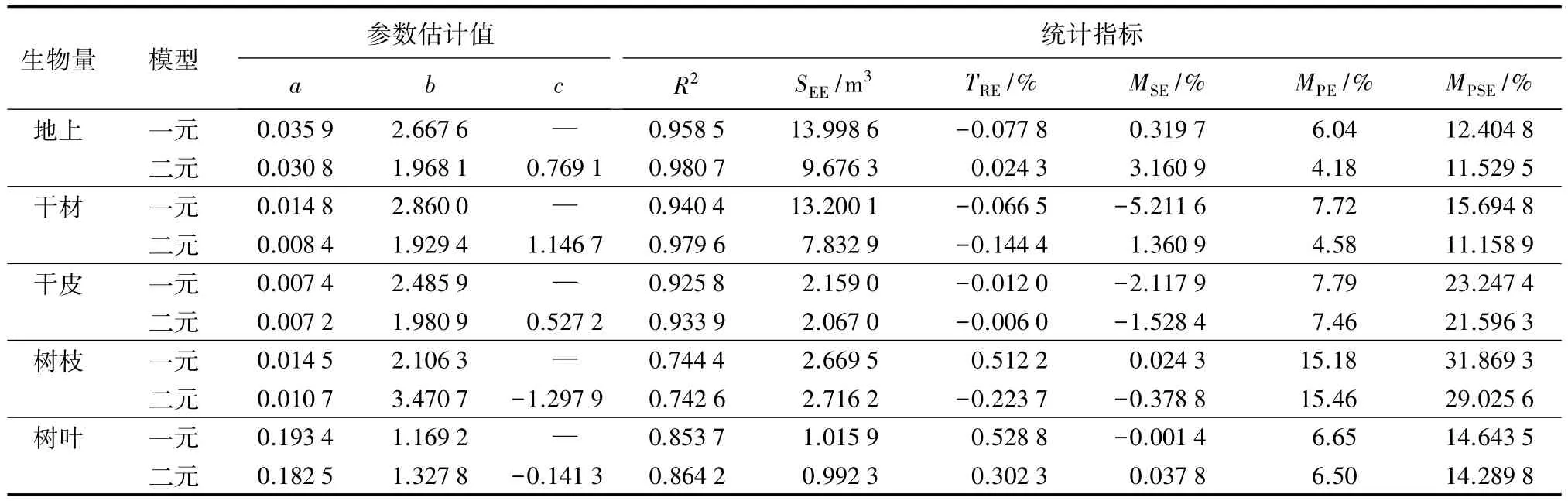
表3 独立模型的参数估计值和统计指标

3.2 相容性模型拟合结果

利用总生物量直接控制所建立的总量与各分量相容性生物量模型的参数估计值以及模型的统计指标(见表4～5)。

表4 相容性模型的参数估计值

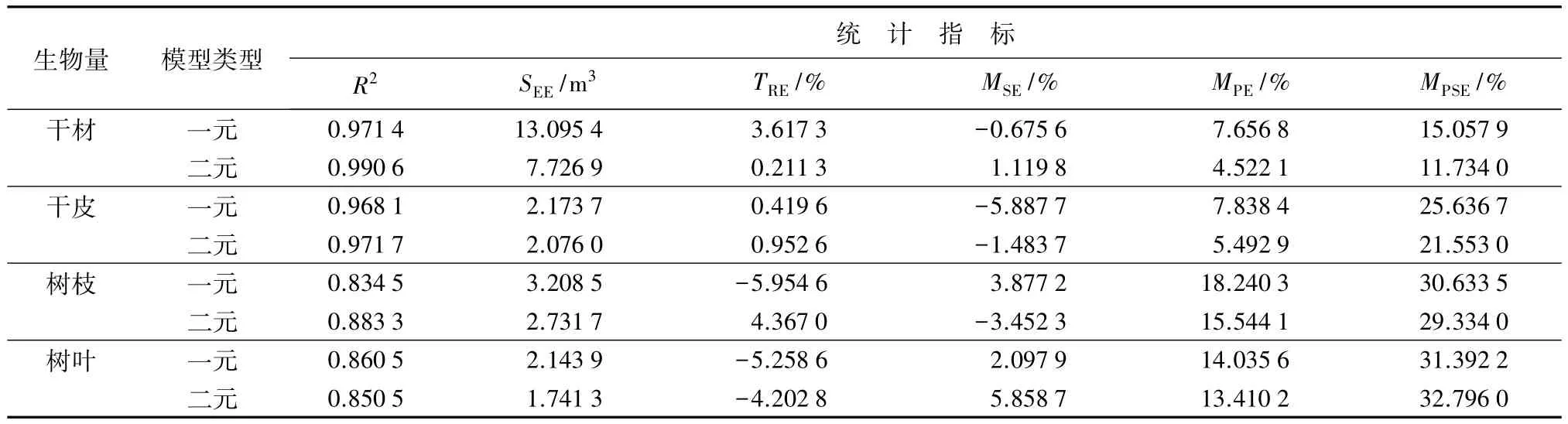
表5 相容性模型的统计指标

对于一元相容性模型，干材、干皮的确定系数R2均较高，分别超过了97%和96%，而树枝和树叶的R2相对较低，但也分别超过了83%和86%，各分量的总相对误差(TRE)和平均系统误差(MSE)均在±6%以内，模型拟合效果良好。而采用二元模型，各分量的统计指标都有不同程度的改进，干材的确定系数R2超过99%，说明解释变量的增加，干材生物量与胸径和树高的关系已近似于线性，其估计值的标准差(SEE)更是降低了40%以上，提高了拟合优度;各分量的平均预估误差(MPE)均在80%以上，相对误差(TRE)和平均系统误差(MSE)都略有减小，拟合效果总体上优于一元模型。

对比地上各部分生物量的独立估计和利用度量误差模型进行的联合估计，各项统计指标整体上都有所改进，但改进不大，说明联合估计主要是协调和解决各个分量之间的比例关系，使总量和各分量达到了相容性。建立的一元相容性模型已经很好的满足了预估精度的要求，随着解释变量的增加，二元模型主要是改进了干材生物量的估计，对其他分量的预估精度提高很少。从模型的有效性和实用性角度考虑，采用一元生物量模型来估计大尺度范围的森林生物量是合适的，而要得到更高精度的估计值，则可以考虑采用二元生物量模型。

3.3 各分量所占比例变化

根据一元相容性生物量方程系统及表4的参数估计值结果，可以对各个分量占地上总生物量的比例随林木直径的变化进行分析(见图1)。由图1可知。杉木干材生物量占地上总生物量的比例随林木直径的增大而升高，从2 cm的35%逐渐提高到60 cm的72%;干皮、树枝和树叶生物量所占比例均随林木直径的增大而下降，其中干皮、树枝生物量所占比例下降相对平缓，分别从2 cm的18%和19%下降到60 cm的9%和13%，而树叶生物量所占比例下降趋势较为明显，从2 cm的27%下降到60 cm的6%。

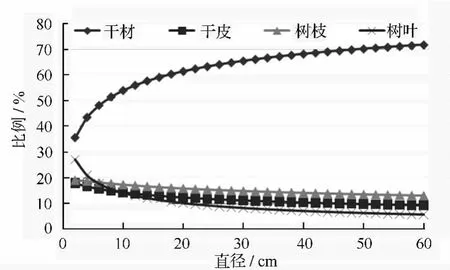
图1 杉木各分量所占比例随直径的变化

4 结论

以福建将乐人工杉木地上生物量实测数据为基础，利用非线性度量误差模型方法，建立了地上生物量和干、皮、枝、叶4个分项生物量的独立方程和相容性方程系统，并对各个分量所占比例变化特点进行了分析。得到结论如下:

以地上总生物量为基础构建相容性方程系统，采用总量直接控制方案可以有效拟合相容性方程，所得模型结构简单，参数稳定，拟合精度高。

对地上总生物量模型的估计，可以采取独立估计和联合估计2种处理方法，结果表明2种方法的预估结果差异不大，都是行之有效的建模方案，但联合估计可以有效解决总量与各分量之间的相容性问题。因此，在进行生物量估算时，可以先建立地上生物量模型，再将其预估结果代入相容性方程系统，用度量误差模型方法求解其他4个分量模型的参数。

通过对一元和二元模型的对比分析，一元模型能够很好的满足建模需求。随着解释变量的增加，估计值的标准差和平均预估误差会有所下降，确定系数有所上升，总体上二元模型略优于一元模型。从模型的有效性和实用性角度考虑，采用一元生物量模型来估计大尺度范围的森林生物量是合适的，而要得到更高精度的预估值，则可以考虑二元生物量模型。

杉木各个分量占地上总生物量的比例随直径的增加而呈现不同的变化特点，其中:干材生物量占地上总生物量的比重随林木直径的增加而提高;干皮、树枝和树叶生物量占地上总生物量的比重随林木直径的增加而逐渐下降，树叶生物量占地上总生物量的比重下降较为明显，而干皮和树枝的下降趋势相对平缓。

本文所建立的一元相容性生物量方程系统，地上总生物量、干材生物量和干皮生物量预估精度均达到95%以上，树枝和树叶生物量的预估精度也接近90%;二元相容性生物量方程系统的预估精度还要更高一些。由于所用实验数据均采集于福建省将乐国有林场人工杉木纯林，且仅限于地上生物量部分，建立的地上生物量方程与地下生物量方程的相容性，及其在其他地区和其他树种的适用性还需进一步讨论和验证。

[1]董利虎，李凤日，贾炜玮.东北林区天然白桦相容性生物量模型[J].林业科学，2013，49(7):75－85.

[2]曾伟生.全国立木生物量方程建模方法研究[D].北京:北京林业大学，2011.

[3]Fang J Y，Wang Z M.Forest biomass estimation at regional and global levels，with special reference to China’s forest biomass[J].Ecological Research，2001，16(3):587－592.

[4]Cronan C S.Belowground biomass，production，and carbon cycling in mature norway spruce，maine，U.S.A[J].Canadian Journal ofForest Research，2003，33:339－350.

[5]Muukkonen P.Forest inventory-based large-scale forest biomass and carbon budget assessment:new enhanced methods and use of remote sensing for verification[R].Finland:Department of Geography，University of Helsinki，2006.

[6]Woodbury P B，Smith J E，Heath L S.Carbon sequestration in the U.S.Forest sector from 1990 to 2010[J].Forest Ecology and Management，2007，241(1/3):14－27.

[7]王轶夫，孙玉军.马尾松生物量模型的对比研究[J].中南林业科技大学学报，2012，32(10):29－33.

[8]曾伟生，唐守正.利用度量误差模型方法建立相容性立木生物量方程系统[J].林业科学研究，2010，23(6):797－803.

[9]骆期邦，曾伟生，贺东北，等.立木地上部分生物量模型的建立及其应用研究[J].自然资源学报，1999，14(3):271－277.

[10]唐守正，张会儒，胥辉.相容性生物量模型的建立及其估计方法研究[J].林业科学，2000，36(1):19－27.

[11]Parresol B R.Additivity of nonlinear biomass equations[J].Canadian Journal of Forest Research，2001，31(5):865－878.

[12]Bi H Q，Turner J，Lambert M J.Additive biomass equations for native eucalypt forest trees of temperate australia[J].Trees，2004，18(4):467－479.

[13]Tang S Z，Li Y，Wang Y H.Simultaneous equations，error-invariable models，and model integration in systems ecology[J].Ecological Modelling，2001，142(3):285－294.

[14]Tang S Z，Wang Y H.A parameter estimation program for the error-in-variable model[J].Ecological Modelling，2002，156(2/3):225－236.

[15]唐守正，李勇.生物数学模型的统计学基础[M].北京:科学出版社，2002.

[16]李永慈，唐守正.带度量误差的全林整体模型参数估计研究[J].北京林业大学学报，2006，28(1):23－27.

[17]曾伟生，夏忠胜，朱松，等.贵州人工杉木相容性立木材积和地上生物量方程的建立[J].北京林业大学学报，2011，33(4):1－6.

[18]方宗辉.福建省杉木人工林生物量及其分配研究[J].福建林业科技，2005，32(3):82－85.

[19]魏晓慧，孙玉军，马炜.基于Richards方程的杉木树高生长模型[J].浙江农林大学学报，2012，29(5):661－666.

[20]孙玉军，张俊，韩爱惠，等.兴安落叶松(Larix gmelini)幼中龄林的生物量与碳汇功能[J].生态学报，2007，27(5):1756－1762.

[21]俞月凤，宋同清，曾馥平，等.杉木人工林生物量及其分配的动态变化[J].生态学杂志，2013，32(7):1660－1666.

[22]付尧，马炜，王新杰，等.小兴安岭长白落叶松相容性生物量模型的构建[J].东北林业大学学报，2011，39(7):42－45.

[23]Chojnacky D C.Allometric scaling theory applied to FIA biomass estimation:GTR NC－230[R].North Central Research Station，Forest Service USDA，2002:96－102.

[24]唐守正，郎奎建，李海奎.统计和生物数学模型计算(ForStat教程)[M].北京:科学出版社，2008.

[25]曾伟生，唐守正.立木生物量方程的优度评价和精度分析[J].林业科学，2011，47(11):106－113.