基于特征系统实现算法的输电塔气动阻尼风洞试验研究

段成荫，邓洪洲

(同济大学 建筑工程系，上海 200092)

输电塔是一种由角钢或钢管通过螺栓连接或焊接组成的格构式结构，相较于较小的结构阻尼，气动阻尼对输电塔结构风振响应具有较大的影响。通常的观点是结构气动阻尼与风速之间存在较强的依赖性，根据准定常理论顺风向气动阻尼应与来流平均风速(或折减风速)成正比［1］，近年来一些气动阻尼风洞试验研究正是基于这一关系同时考虑其他可能的影响因素如风场类型［2］、结构阻尼［3］、结构外形［4－6］等开展了一些工作，但这些研究的对象是高层建筑或者大跨屋盖这些钝体外形的结构。格构式输电塔迎风面密实度较低，杆件之间存在互相影响，气动阻尼比较离散［7］。虽然顺风向气动阻尼随风速有增大趋势［8］，但与准定常假定是否相符仍需进一步的验证，根据Takeuchi等［7］的实测研究，气动阻尼并非随风速增大而成比例地增大。而且由于输电塔气动外形与传统的钝体相去甚远，不太可能发生整体涡振现象，其横风向气动阻尼可能与高层建筑出现负值［9］的规律有所不同。

特征系统实现算法(Eigensystem Realization Algorithm，ERA)［10］是一种基于状态空间的时域模态参数识别方法，利用系统脉冲响应函数或者相关函数得到系统的最小实现。ERA识别模态参数仅需很短的响应历程，识别速度快，对密频模态的识别效果好，得到了很多研究者的重视并且发展出了诸如ERA/DC(Eigensystem Realization Algorithm using Data Correlation)［11］、FERA(Fast ERA)［12］等改进算法。然而ERA也存在抗噪能力差的缺点，往往会出现大量的虚假模态，模型定阶和系统真实模态的提取目前尚未形成完善的理论，识别过程中仍存在一定主观因素的影响。

本文首先对特征系统实现算法中虚假模态的剔除问题进行了研究，提出模态参与因子(Modal Participation Factor，MPF)作为识别真实模态与虚假模态的一个指标，并给出了估算模态能量贡献(Modal Energy Contribution，MEC)的简化计算公式，基于MPF和MEC采用自动识别程序对一输电塔气弹模型环境激励下的模态参数进行识别，得到了不同风向角下模型两个主轴方向的气动阻尼，并研究了其与来流平均风速的关系。

1 模态参数识别与提取

1.1 特征系统实现算法

由Juang等人［10］提出的特征系统实现算法(ERA)基于系统的离散时间域状态空间模型，利用脉冲响应序列即Markov参数的特点，构造Hankel矩阵:

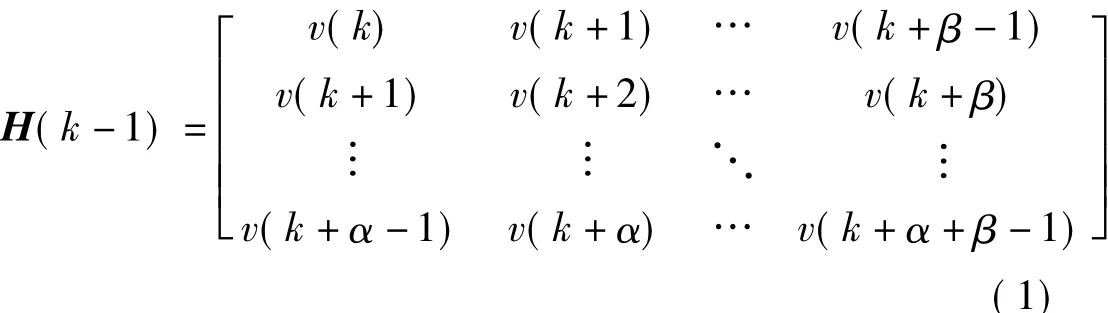
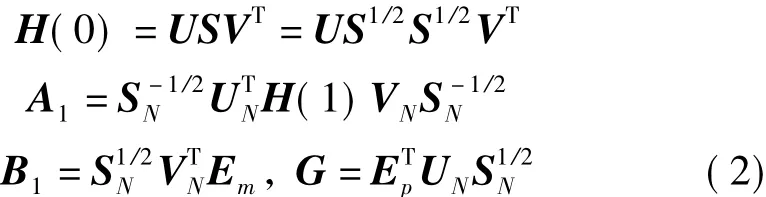
式中，S 为对角阵，U、V 为酉阵，SN、UN、VN为最大的前N 个奇异值所对应的子矩阵，Em=［Im，O，…，O］T，Ep=［Ip，O，…，O］T，m 为外激励数，p输出通道数，I为单位矩阵，O为零矩阵。

通过对A1进行特征值分解得到以共轭对的形式出现的特征值 λ1，λ2，…，λn，…。

从而模态的频率和阻尼比可以通过如下方法计算，Δt为采样间隔:

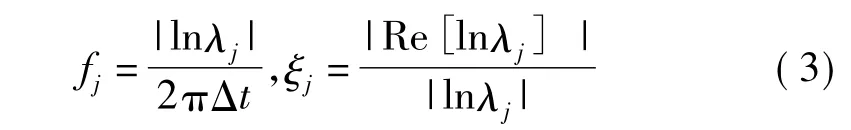
总阻尼减去结构阻尼即为气动阻尼:

为了提高ERA识别的抗噪能力，本文采用脉冲响应的相关系数r(k)来代替脉冲响应v(k)构造Hankel矩阵，能有效抑制噪声影响［15］:

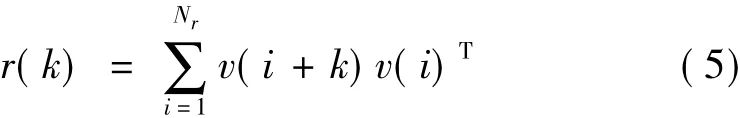
式中，Nr为相关数据长度。秦仙蓉等［13］指出在10%和30%的噪声下ERA/DC算法比ERA精度高6～60倍。

1.2 随机减量技术——RDT

ERA算法的关键就是根据系统的脉冲响应序列集成Hankel矩阵，脉冲响应可基于实测信号(位移、速度、加速度等)采用随机减量技术(Random Decrement Technique，RDT)［14］得到。随机减量技术利用随机响应中由系统固有特性决定的确定性成份和由环境激励决定的随机成份二者在统计上的不同性质，通过指定某种合理条件，然后采用平均的方法将随机成份滤掉从而分离出自由衰减信号。

如果选取适当的阈值x=x0去截取该样本曲线x(t)，交点对应的时刻ti(i=1，2，…)，可得到一系列从ti时刻开始的子样本曲线xi(t)，每条子样本曲线可看成由ti时刻初位移、初速度引起的自由振动和从ti时刻开始随机激励引起的强迫振动三部分组成，RDT通过对各条子样本曲线xi(t)作算数平均得到自由衰减信号。

1.3 模态识别指标

受各种噪声影响，环境激励下结构响应通过ERA计算出来的模态成份是十分丰富的，如何提取系统的真实模态是ERA应用中的一个问题，通常提取较大奇异值所对应的模态，但这种做法仍无法有效剔除虚假模态，特别是无法对结果进行归类和自动提取。

文献［15］认为各阶传递函数的全频域积分可作为衡量各阶模态能量贡献MEC的指标:

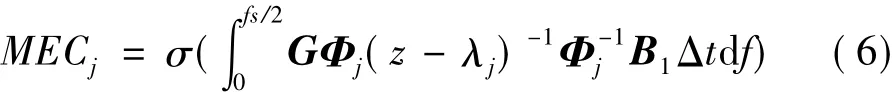
式中，Ф为A1的特征向量矩阵，fs为采样频率，Δt为采样间隔，"(·)表示求最大奇异值。式(6)虽然可以反映模态的能量水平，但需要进行全频域的积分运算，运算量较大，而且如果虚假模态阻尼比很小，采用式(6)仍难以判断。

系统的脉冲响应可分解为各阶模态之和:

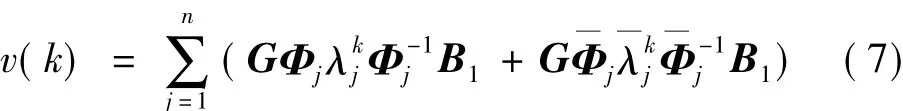
经推导各阶信号vj经可写为:

可见，v(k)为代表各阶模态的脉冲信号之和，MPF恰为各阶信号的初始振幅，根据MPF的大小可分离各阶模态，理论上噪声模态MPF应接近于0，因此前若干阶MPF对应的模态即为系统真实模态。

各阶模态的能量贡献式(6)可以用更为简单的估算公式表示为:

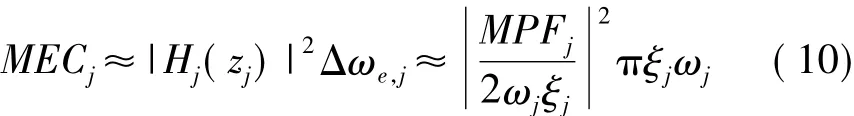
Δωe，j= πξjωj为传递函数的白噪声带宽，由式(9)和式(10)可见，MEC与识别的频率和阻尼比有很大关系，当阻尼比很小时(通常为噪声模态)MEC将很大，而MPF则是与频率和阻尼比无关的振幅，因而可以避免小阻尼虚假模态共振峰的干扰。

1.4 模态参数提取步骤

本文对于ERA识别结果的提取过程如下:

(1)计算各识别结果的MPFj和MECj;

(2)若MPFj＞阈值则保留，否则判定为虚假模态，为不至于发生遗漏，阈值的选取应使保留模态数量大于系统阶次;

(3)根据MPF大小对保留模态进行排序，若某两个结果的MPF比较接近则根据其MEC排序，即可区分不同阶次模态参数;

(4)最后，将不同Hankel阵阶次下的提取结果形成稳定图，确定是否为有效识别结果，并取平均值输出为模态参数提取值。

该程序基本可以由计算机自动完成，能提高识别效率以及减小人工干预的主观影响。

表1 模型主要相似比Tab.1 Main scales for the model

2 风洞试验概况

风洞试验的原型为一双回路500 kV输电塔，总高度101 m。气弹模型的缩尺比和风速比根据风洞试验段的大小分别定为λL=1/80和λL=1/3(模型/原型，下同)，模型主要相似比见表1。

如图1所示，定义水平横担的方向为X向，垂直于横担方向为Y向，定义风向角为来流方向与Y轴的夹角，加速度传感器布置在模型下横担处X向和Y向。

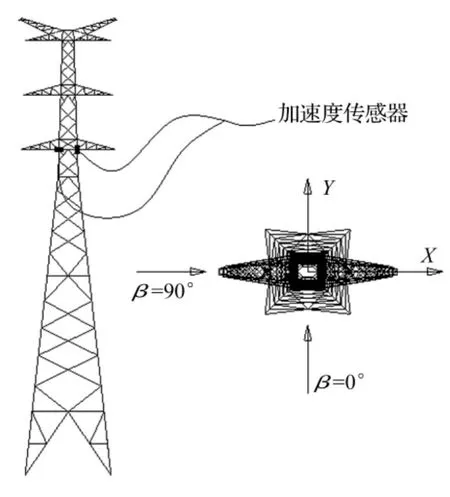
图1 测点布置和坐标定义Fig.1 Model instrumentation and coordinate definition

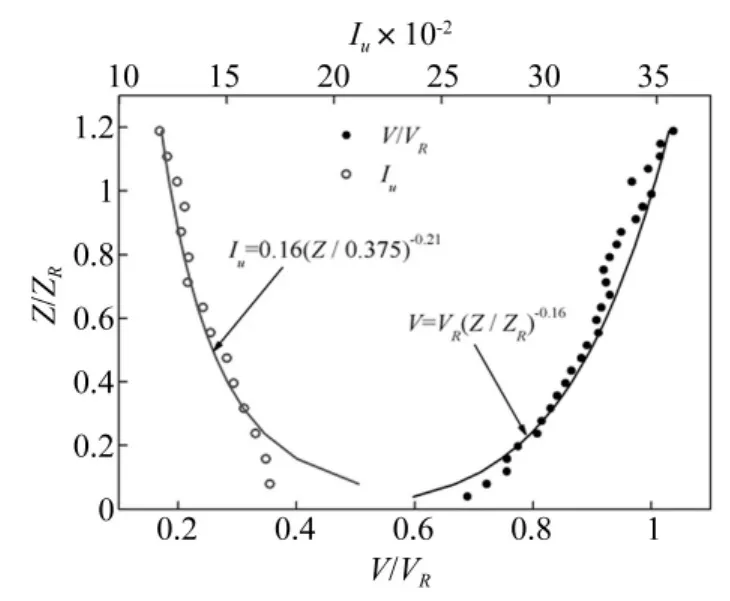
图2 风剖面和紊流度剖面Fig.2 Simulated mean velocity and turbulence intensity profiles

通过人工激振法得到的模型动力特性如表2所示，表中理论值表示ANSYS模态分析结果。

表2 模型动力特性Tab.2 Eigenvalues of the model

试验在同济大学TJ－3低速边界层风洞进行，试验风剖面指数接近于α=0.16，紊流度接近于30 m(模型0.375 m)高紊流度Iu=16%，试验风剖面和紊流度剖面如图2所示。

试验分别在 0°、15°、30°、45°、60°、75°、90°七个风向角下进行，风速范围为4～11 m/s，采样频率250 Hz，采样时长69.632 s，样本容量17 408，控制风速的参考高度ZR位于模型顶部高度1.263 m。

3 结果分析与讨论

3.1 模态提取

以0°风向6.24 m/s风速下Y向加速度识别为例，其功率谱如图3(a)所示，采用60阶Hankel矩阵时各模态的MEC谱和MPF谱见图3(b)和(c)。最大MEC(0.034)对应的频率为97 Hz，甚至大于32 Hz处真实模态的值(0.022)，但在功率谱图3(a)中97 Hz附近并无显著共振峰，因此为噪声模态，结合式(10)不难看出其MEC过大的原因就在于阻尼比识别值4.6×10－6很小。图3(c)中97 Hz处识别结果的MPF仅为0.011，表明该阶信号振动幅度很小，确为虚假模态，32 Hz处MPF(0.33)明显大于其他值，故判定其代表一阶真实模态，至于高阶模态是否存在从图3(c)的单一结果中无法确定，因此保守地提取MPF最大的前三个结果，并将不同Hankel阵阶次下的提取值形成稳定图。

图3 奇异值谱(a)、MEC谱(b)和MPF谱(c)Fig.3 Spectra of singular value(a)，MEC(b)and MPF (c)

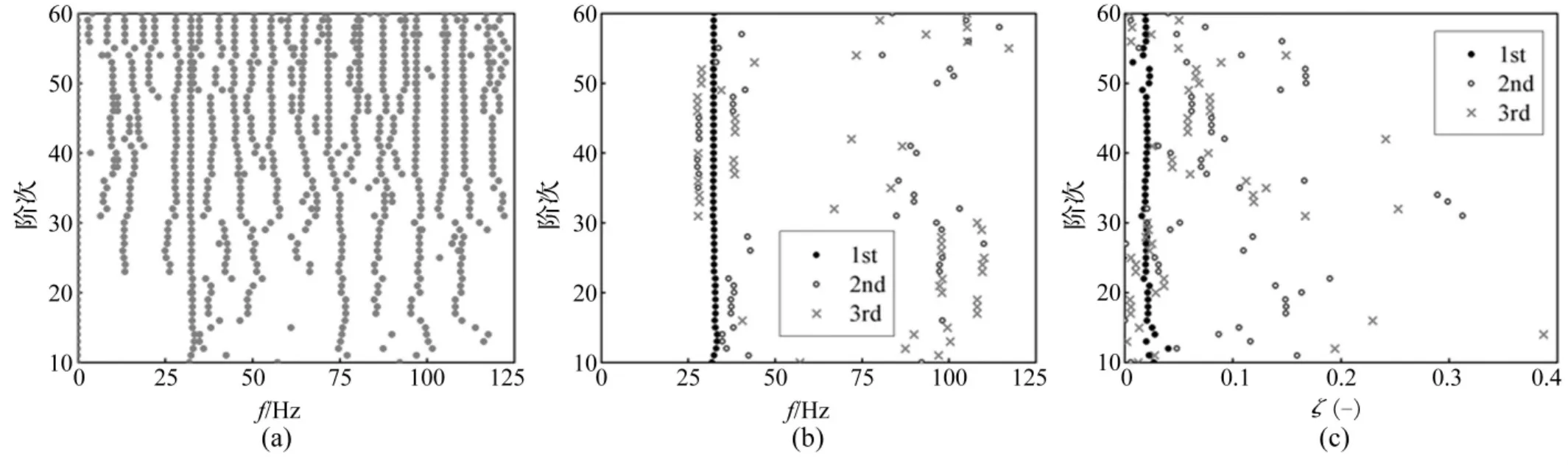
图4 剔除前稳定图(a)和按本文方法提取的前三阶频率(b)、阻尼比(c)稳定图Fig.4 Stabilization diagrams of original results(a)，the first three identified frequencies(b)and damping ratios(c)

图4 为模态参数识别结果的稳定图。图4(a)为不经任何处理的ERA结果，频率成份十分丰富，难以直接从稳定图中辨别真实模态。图4(b)和图4(c)为按本文识别方法提取最大三个MPF对应的频率和阻尼比稳定图，一阶显然是真实模态，频率十分稳定，阻尼比偏差稍大但也基本保持常数，二、三阶则并不稳定，只能准确识别一阶物理模态。原因一方面是对于输电塔这类高耸结构，其一阶弯曲模态通常占有统治地位，高阶模态的参与程度很小，很可能被噪声所掩盖;另一方面试验时为了避免加速度传感器和数据线对模型造成太大影响，测点布置在塔身中部偏上，该处与二阶弯曲振型的节点接近，难以识别二阶模态。总而言之，本文提出的判别指标MPF对真实模态进行提取的方法是行之有效的，提取过程中人工干预很少，大大减小了识别过程中的主观因素。

3.2 气动阻尼结果与讨论

对输电塔模型环境激励下0°～90°风向角、4～11 m/s平均风速下X向和Y向各工况的1阶频率和阻尼比的识别结果如图5～6图所示。

X向和Y向一阶频率如图5(a)和图6(a)所示，两个方向频率基本相当，各工况处于31.2～33.2 Hz之间，这与表2中采用人工激振法识别的频率基本一致。频率与平均风速有较强的相关性，但与风向角没有明显的关系，频率随着风速的增大而降低，各风向角下均呈现相同趋势，体现空气附加质量和气动刚度对输电塔振动频率具有一定影响。

图5(b)和图6(b)为X向和Y向的一阶阻尼比识别结果。绝大多数工况的阻尼比大于表2给出的1.4%，气动阻力大多以正阻尼的形式存在，这对结构是有利的。但各工况阻尼比的离散性较大，与风速也并非线性关系，在不同风向角下的变化曲线也各不相同。但是图5(b)的 X 向阻尼比在60°、75°、90°风向角下随着风速增大呈上升的趋势，而 0°、15°、30°风向角下基本在一个定值附近波动。图6(b)的Y向阻尼比则相反，0°、15°、30°风向角下随风速增大而增大，60°、75°、90°风向角下基本保持定值。注意到对X向90°角是顺风向而对Y向0°角是顺风向，两个方向以0°和90°为代表的纵横向气动阻尼与风速的关系如图5(c)和图6(c)所示。可见对于顺风向气动阻尼，输电塔结构仍与高层建筑随风速(折减风速)增大而单调递增［16］具有相同的变化趋势;但在横风向，识别结果中并未观察到明显的气动负阻尼，而是基本在0或者较小的水平周围，这是与高层建筑［9，16］不同的特点，原因是输电塔由于格构式的结构特点难以发生整体涡振，横风向仍以结构阻尼为主。

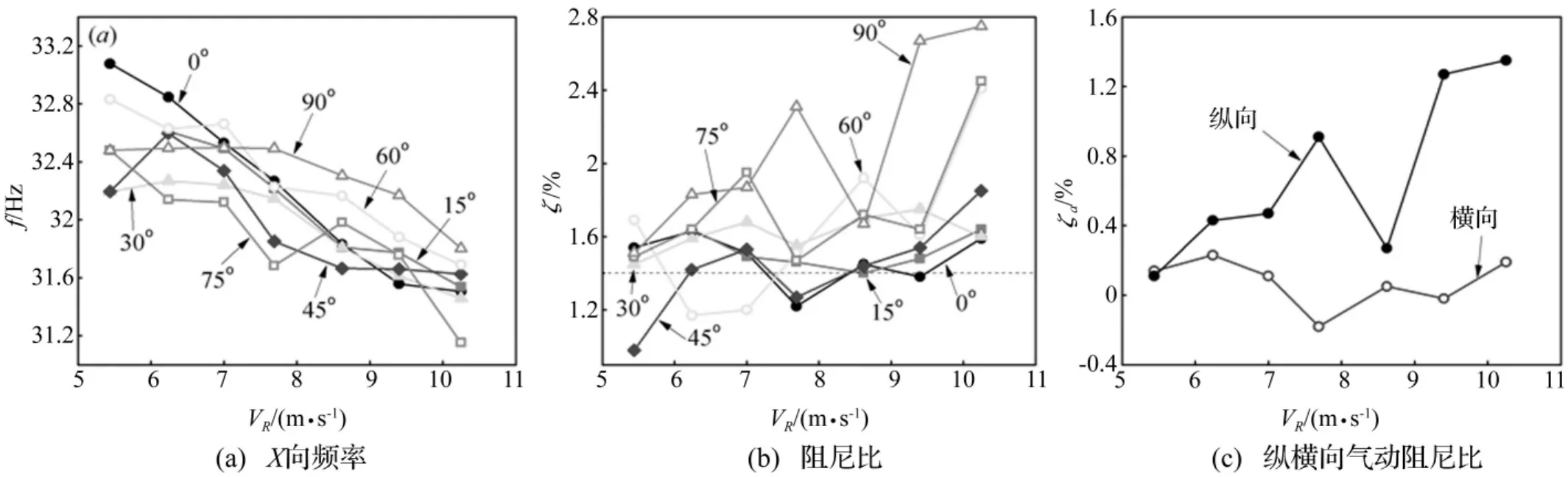
图5 模型识别结果Fig.5 Model identification results

图6 模型识别结果Fig.6 Model identification results

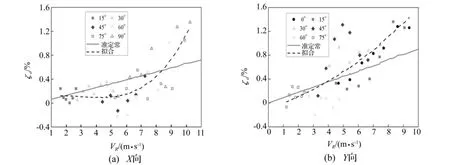
图7 气动阻尼与相应风速分量的关系Fig.7 Model’s aerodynamic damping versus corresponding wind speed components

如前文所述，在不同风向角下气动阻尼与风速的关系各异，很难用一个统一的公式进行描述，但X和Y向气动阻尼在相近角度呈现出相似的规律，表明其与风向角存在某种内在联系，一个最直接的考虑就是X、Y两主轴的气动阻尼与相应方向的平均风速分量的关系。

从图7可以看出，X和Y向气动阻尼与相应风速分量呈正相关关系，相关系数分别为0.623 8和0.774 0，线性相关性仍然不强。图中同时给出了根据准定常理论［1］的气动阻尼取值:

式中，ρ为空气密度;f为一阶模态频率;m(z)为z高度处质量;面积A(z)分别采用正侧面投影面积;平均风速(z)取试验风剖面;阻力系数CD根据司瑞娟［20］的研究取1.5;振型φ采用理论分析的一阶振型系数。准定常理论大体能反映试验气动阻尼的变化趋势，取值也跟多数试验结果相当，但在较高风速时有所低估。Gabbai等［18］提出气动阻力可能与相对风速的N次方(而非准定常假定的平方)成正比，这个关系虽然物理意义不如准定常假定明确，但从图7来看，输电塔结构气动阻尼的确表现出了一些高阶效应，因此这里在准定常理论的基础上增加平均风速的高阶项来表示气动阻尼的趋势:

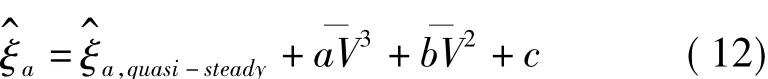
式中，a，b，c为拟合参数，见表3所示。两个方向通过式(12)计算的结果亦绘于图7中，该取值比准定常理论更为准确地表现了气动阻尼与风速分量的变化趋势。

表3 拟合参数和标准误差Tab.3 Fitted parameters and standard error

4 结论

(1)提出了一个用以提取ERA识别结果中真实模态的参数MPF，具有明确的物理意义:从信号的角度讲，MPF代表组成脉冲响应的各阶调幅信号的初始振幅;从系统的角度来讲，MPF代表系统各阶模态的参与程度。

(2)给出了计算模态能量贡献MEC的简化公式，根据MPF和MEC可以有效地剔除虚假模态并自动提取真实模态，降低了识别过程中的主观因素。

(3)环境激励下输电塔一阶频率随风速的增加而略有减小，空气附加质量和气动刚度对输电塔结构具有一定影响。

(4)输电塔气动阻尼大多为正，顺风向随风速的增大呈增大趋势，横风向未出现明显的负阻尼，而是在较小的取值周围波动。

(5)角度风下X、Y方向气动阻尼与相应方向的平均风速分量正相关，但线性关系不强，准定常理论能反映气动阻尼的大体趋势，在较高风速时有所低估。在准定常理论的基础上增加高阶项能更准确地表现试验结果的变化。

［1］Holmes J D.Along-wind response of lattice towers.Ⅱ:Aerodynamic damping and deflections［J］.Engineering Structures，1996，18(7):483－488.

［2］曹会兰，全涌，顾明.风场类型对方形超高层建筑顺风向气动阻尼的影响研究［J］.振动与冲击，2012，31(16):22－26.CAO Hui-lan，QUAN Yong，GU Ming.Effect of roughness exposure on aerodynamic damping of square high-rise buildings［J］.Journal of Vibration and Shock，2012，31(16):22－26.

［3］曹会兰，全涌，顾明，等.独立矩形截面超高层建筑的顺风向气动阻尼风洞试验研究［J］.振动与冲击，2012，31(5):122－127.CAO Hui-lan，QUAN Yong，GU Ming，et al.Effect of roughness exposure on aerodynamic damping of square highrise buildings［J］.Journal of Vibration and Shock，2012，31(5):122－127.

［4］曹会兰，全涌，顾明.一类准方形截面超高层建筑顺风向气动阻尼［J］.振动与冲击，2012，31(22):84－89.CAO Hui-lan， QUAN Yong， GU Ming. Along-wind aerodynamic damping of high-rise buildings with aerodynamically modified square cross-sections［J］.Journal of Vibration and Shock，2012，31(22):84－89.

［5］楼文娟，卢旦，杨毅，等.开孔建筑屋盖风振响应中的气动阻尼识别［J］.空气动力学报，2007，25(4):419－424.LOU Wen-juan，LU Dan，YANG Yi，et al.Identification of aerodynamic damping for roof wind-induced response of opening building［J］.Acta Aerodynamica Sinica，2007，25(4):419－424.

［6］潘峰，孙炳楠，楼文娟.基于Hilbert-Huang变换的大跨屋盖气动阻尼识别［J］.浙江大学学报(工学版)，2007，41(1):65－70.PAN Feng，SUN Bing-nan，LOU Wen-juan.Aerodynamic damping identification of long-span roof based on Hilbert-Huang transform ［J］. Journal of Zhejiang University(Engineering Science)，2007，41(1):65－70.

［7］Takeuchi M，Maeda J，Ishida N.Aerodynamic damping properties of two transmission towers estimated by combining several identification methods［J］. Journal of Wind Engineering and Industrial Aerodynamics，2010，98(12):872－880.

［8］任坤，李正良，肖正直，等.环境激励下特高压输电塔线体系气动阻尼的识别［J］.重庆工学院学报(自然科学版)，2009，23(7):64－68.REN Kun， LI Zheng-liang， XIAO Zheng-zhi， et al.Aerodynamic damping identification of UHV transmission line system under ambient excitation［J］.Journal of Chongqing University of Technology(Natural Science)，2009，23(7):64－68.

［9］吴海洋，梁枢果，陈政清，等.强风下方截面高层建筑横风向气动阻尼比研究［J］.工程力学，2010，27(10):96－103.WU Hai-yang，LIANG Shu-guo，CHEN Zheng-qing，et al.Research on the aerodynamic damping ratios of square tall buildings in across-wind direction under strong wind［J］.Engineering Mechanics，2010，27(10):96－103.

［10］ Juang J N，Pappa R S.An eigensystem realization algorithm for modal parameter identification and model reduction［J］.Journal of Guidance，Control and Dynamics，1985，8(5):620－627.

［11］ Juang JN，Cooper JE.An einginsystem realization algorithm using data correlation(ERA/DC) for model parameter identification［J］.Control Theory and Advanced Technology，1988，4(1):5－14.

［12］刘福强，张令弥.一种改进的特征系统实现算法及在智能结构中的应用［J］.振动工程学报，1999，12(3):316－322.LIU Fu-qiang，ZHANG Ling-mi.An improved eigensystem realization algorithm and its application to modal parameter identification of intelligent space trusses［J］.Journal of Vibration Engineering，1999，12(3):316－322.

［13］秦仙蓉，王彤，张令弥.模态参数识别的特征系统实现算法:研究与比较［J］.航空学报，2001，22(4):340－342.QIN Xian-rong，WANG Tong，ZHANG Ling-mi.Comparison of different variants of the eigensystem realization algorithm in modal parameter identification［J］.Acta Aeronautica Et Astronautica Sinica，2001，22(4):340－342.

［14］ Cole H A J.Methods and apparatus for measuring the damping characteristics of a structure: United States，3620069［P］.1971－11－16.

［15］章国稳，汤宝平，潘飞.特征系统实现算法的虚假模态剔除方法［J］.重庆大学学报，2012，35(3):20－25.ZHANG Guo-wen，TANG Bao-ping，PAN Fei.The method for removing the spurious modes of eigensystem realization algorithm［J］.Journal of Chongqing University，2012，35(3):20－25.

［16］全涌，顾明.方形断面高层建筑的气动阻尼研究［J］.工程力学，2004，21(1):26－30.QUAN Yong， GU Ming. Wind tunnel test study of aerodynamic damping of super highrise buildings［J］.Engineering Mechanics，2004，21(1):26－30.

［17］司瑞娟.特高压输电塔线体系风振响应及抗风设计参数研究［D］.上海:同济大学，2011.

［18］ Gabbai R D，Simiu E.Aerodynamic damping in the alongwind response of tall buildings［J］.Journal of Structural Engineering，2010，136(1):117－119.