高精度航天器太阳能电池阵减扰驱动方法

朱仕尧，雷勇军，谢 燕，李家文

(国防科学技术大学 航天科学与工程学院，长沙 410073)

现代三轴稳定卫星一般均装配有大型柔性太阳能电池阵结构。为保证其在全轨道周期内获得最大受晒面积，卫星本体与电池阵安装界面处通常会增加驱动装置以实现电池阵法线对太阳的跟踪驱动。然而在内外诸多因素作用下，跟踪驱动会激起电池阵柔性振动与摩擦力矩波动。尽管这部分扰动幅值较小，但对于指向精度或成像精度要求较高的航天器，太阳能电池阵跟踪驱动已经成为影响其技术性能指标的重要因素之一。“国际通信卫星V”、美国“高层大气研究卫星”和日本“先进陆地观测卫星”等多颗卫星都曾因此出现运行事故。

在电池阵减扰驱动方面，Doherty等［1］首先将输入成形方法应用于电池阵减扰驱动策略规划，Freitas［2］进一步通过地面试验证明该方法在电池阵跟踪驱动过程中的减扰效果。2006年GOES-N卫星对基于输入成形方法的电池阵驱动策略进行在轨测试，并最终将其作为电池阵长期驱动策略［3］。朱春燕等［4－5］将这一方法应用于电池阵调姿驱动过程。然而以上输入成形方法仅适用于抑制间歇式驱动策略中的残余振动，不适合转速极低且持续驱动的电池阵连续驱动状态。针对这一问题，赵江涛［6］通过附加力矩补偿机构对电池阵驱动过程所引起的扰动进行力矩补偿。张猛等［7］对电机力矩成分进行分析，并提出在绕组参考电流中引入补偿项来改善驱动装置的速度稳定度。陆栋宁等［8］采用Lyapunov方法设计了基于输出反馈的驱动装置闭环驱动控制器。

在以上研究基础上，本文基于考虑负载柔性、摩擦力矩、齿槽效应以及电流环控制等因素的电池阵及其驱动装置的机电一体化模型，首先分析在电池阵驱动过程中激扰其产生转速和扰动力矩波动的主要因素;根据分析结论，从稳态力矩平衡方程出发，通过公式推导分别得到采用闭环输入补偿和开环输入补偿方式的两种减扰驱动方法，并对其减扰效果以及参数敏感度进行对比分析，结果证明两种减扰驱动方法都能够有效改善电池阵跟踪驱动过程中的速度和力矩稳定度。

图1 电池阵驱动流程Fig.1 Tracking-drive workflow of solar array

1 电池阵及其驱动装置机电一体化模型

直接驱动型太阳能电池阵工作流程如图1所示，其中包括驱动机构内部伺服控制以及电池阵机械转动驱动等工作环节。驱动伺服控制可根据给定角度得到细分后的绕组参考电流，并通过绕组实际电流反馈控制得到步进电动机驱动电压。其中电机j相绕组参考电流、实际电流以及电流环控制公式如下

式中:和ij为j相绕组中的参考电流和实际电流;uj为j相绕组中的驱动电压;Im为电机绕组额定电流;fs为电机细分驱动频率;t为仿真时间;round(·)为取整函数;Ns为驱动细分数;j为j相绕组电流初始相位;R为绕组电阻;L为绕组自感系数;Km为电机电磁力矩系数;Nm为电机极对数;θm和ωm分别为电动转角和转速;KP、KI和 KD为电流环 P(比例)、I(积分)和 D(微分)等环节的调节增益。

电池阵驱动装置的转子力矩平衡方程为

式中:Te为电机电磁力矩;Tf为装置摩擦力矩;Tl为柔性负载驱动力矩;Km为电机电磁力矩系数;TK为齿槽转矩幅值;Np为电机相数;Jm和Jl分别为电机转子和电池阵转动惯量;η为电池阵模态坐标向量;Fl为电池阵模态振动与刚体转动之间的耦合系数矩阵;Tc为库伦摩擦力矩;σ0为粘性摩擦阻尼系数;sgn(·)为符号函数。

模态坐标下电池阵振动微分方程为

式中:i和Ωi为柔性负载第i阶模态阻尼系数和固有频率。详细推导过程可参考文献［9］。

2 激扰因素分析

分别对刚性和柔性负载条件下的电池阵跟踪驱动过程动态响应进行分析，从中寻找引起驱动过程扰动的主要激扰因素。

2.1 刚性负载状态

采用刚性负载替换柔性电池阵，以0.06°/s平均转速驱动时的计算结果如图2所示。从图2(a)所示的驱动力矩时间历程曲线可以发现:起动5 s后电池阵进入稳定驱动状态，驱动力矩呈现周期性变化，周期约为5 s。进一步通过对转动速度的功率谱(如图2(b)所示)分析可知:转速主要频率成分分布集中在0.2 Hz附近。而驱动装置选用的步进电机齿数为300，两相双四拍驱动时的步距角为0.3°。电机每走一步，齿槽力矩完成一个周期波动，因此0.06°/s转速条件下齿槽力矩的周期为5 s，对应频率正好为0.2 Hz。说明齿槽力矩频率特征与转速功率谱频率曲线峰值对应频率非常吻合。

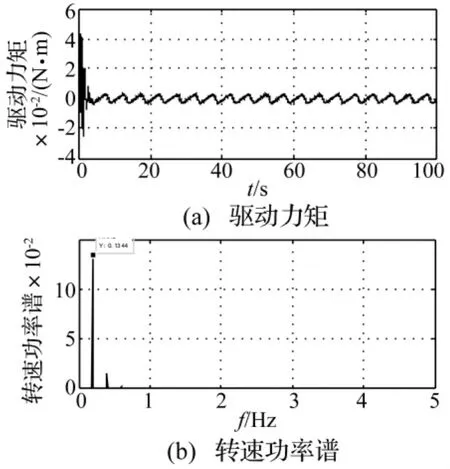
图2 刚性负载状态仿真结果Fig.2 Simulation results on rigid load condition

2.2 柔性负载状态

在以柔性电池阵作为负载条件下对跟踪驱动过程进行仿真分析。图3(a)和(b)分别为不包含(即只有谐波电磁力矩)和包含齿槽力矩情况下电池阵转速和驱动方向扰动力矩时间历程曲线。由图3(a)可知:不考虑齿槽效应时，起动波动过后电池阵转速和扰动力矩逐渐趋于稳定，不会产生周期性波动;而考虑齿槽效应以后(见图3(b))，电池阵的平稳驱动状态下会出现周期性的转速波动，且在两相四拍驱动策略中波动频率是绕组电流频率的4倍。这是因为在以平均角速度驱动的工况下，细分数较大时可以近似认为绕组电流具有正余弦变化规律

将式(9)代入式(5)，整理得

式(10)中第一项对应谐波电磁力矩项，其中TM=KmIm为谐波电磁力矩幅值，(－θm)可以理解为实际角位移与期望角位移之间误差。当误差波动较小时，平稳驱动状态下可以近似将第一项写为TMNmKs(－θm)，其中Ks为角度误差正弦值与角度误差值之比。此时的谐波电磁力矩可以看作是角位移的比例控制环节，TMNmKs为比例增益，该项作用是使电池阵按照指定运动规律转动。而齿槽效应的引入会使电池阵驱动过程发生转速波动，进而引起电池阵的柔性振动和摩擦力矩波动。

图3 包含与不包含齿槽效应时的仿真结果Fig.3 Simulation results with and without cogging effect

图4 齿槽效应对驱动过程的影响Fig.4 Effects of cogging effect on driving process

为描述转速和扰动力矩的波动情况，分别定义转速稳定度σω和力矩稳定度σT为

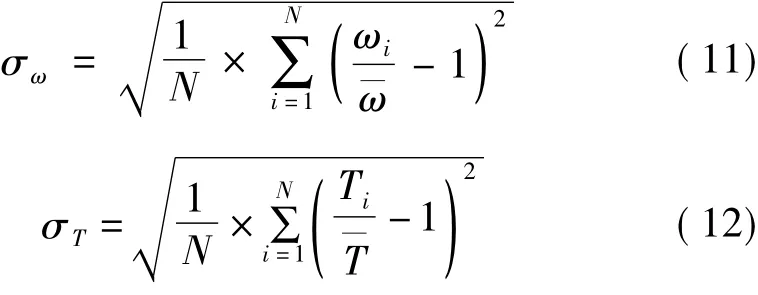
式中:N为采样点数，ωi和Ti分别为采样点i的瞬时转速和扰动力矩，T—为平稳驱动时电机平均力矩，定义T—=σ0ω—+Tc。图4给出不同齿槽力矩状态下的转速和力矩稳定度，从中可以进一步发现转速和扰动力矩稳定度与齿槽定位力矩幅值成正相关关系。

由以上分析可知:步进电机的齿槽效应是引起电池阵驱动过程扰振的主要原因之一，而电机谐波电磁力矩可以近似为电池阵转角的比例控制环节。

3 减扰驱动研究

机电系统消除齿槽效应的方法大致分为两类:一是改进驱动控制方法［10－11］，二是改变定子和转子的齿槽构型和分布［12］。本文从驱动控制方式着手研究电池阵跟踪驱动过程的减扰驱动方法。

3.1 减扰驱动方法

为抵消齿槽效应影响，从稳态驱动状态下的力矩平衡方程出发，通过公式推导分别得到闭环和开环输入补偿角度表达式。

(1)闭环输入补偿减扰驱动方法

在驱动装置中引入闭环控制环节，以电机实际转角θm作为反馈信号，并基于实际转角θm对输入参考角度进行补偿。首先，恒定转速驱动情况下忽略齿槽效应(或抵消齿槽效应后)的力矩平衡方程可以表示为

式中:t为给定参考角度。在没有转速波动的平稳驱动状态下，随着时间增加，和逐渐趋近于零。此时式(13)可以化简为

整理式(18)可得闭环输入补偿角θc为

(2)开环输入补偿减扰驱动方法

目前大多电池阵驱动装置产品均采用开环控制。为避免构建闭环系统的复杂性，考虑对开环控制方法进行改进。对于转速极低且匀速驱动的电池阵跟踪驱动，其运动规律的特殊性往往可以使问题得到简化。整理式(14)得到电池阵转角变化规律(设为θ1)

针对考虑齿槽效应的稳态力矩平衡方程式(15)整理得到参考转角θ0与此时实际转角(设为θ2)之间关系为

预使真实角位移不受齿槽效应的影响，需要参考转角θ0进行修正。将式(20)实际转角θ1代入式(21)中替换实际转角θ2得到

其中第一项为与齿槽力矩同周期变化的波动项，第二项为常数项。图5给出两种减扰驱动方法的系统框图。

图5 减扰驱动方法框图Fig.5 Schematic block diagrams of disturbance-mitigation drive methods

3.2 减扰效果分析

分别采用原始驱动方法(取齿槽力矩幅值为0.06 N·m)和两种改进驱动方法对电池阵驱动过程进行时域仿真，结果如图6所示。从图6(a)和(b)中的计算结果分析可知:驱动装置运行30 s后，电池阵跟踪驱动进入平稳驱动状态;与原始驱动方法相比，两种减扰驱动方法都能够抵消齿槽定位力矩对平稳驱动状态的影响，使转速和扰动力矩的周期性波动幅值明显减小。由其局部放大图还可以发现两种减扰驱动方法驱动下的转速和扰动力矩时间历程存在一定差别。由图6(c)可以对比两种减扰驱动方法对电池阵转动运动规律的影响:驱动方式改进后电池阵转角运动规律变化较小，且转角偏差基本呈周期波动，但波动幅值不足0.01°，说明两种改进驱动方法不会影响电池阵的跟踪指向精度。

图6 电池阵减扰驱动后的仿真结果Fig.6 Simulation results with operation of new drive method

然而由于电池阵及其驱动装置的设计和制造误差，以及电机磨损老化等未建模因素会在一定程度上影响驱动装置的齿槽效应，所以齿槽力矩峰值比K2在卫星全轨道周期内会一定偏差。表1给出两种驱动方法驱动下的转速和力矩稳定度与齿槽力矩峰值误差之间的关系。从中不难发现电池阵驱动扰动力矩和转速波动幅度随齿槽力矩峰值误差绝对值增大而逐渐增大。当齿槽力矩峰值误差为零时，两种减扰驱动方法能够有效改善转速和力矩稳定度，转速稳定度由原始驱动方法下的9.10%减小到0.27%(闭环)和0.16%(开环);力矩稳定度由原始驱动方法下的10.66%减小到0.32%(闭环)和0.21%(开环)。此时开环减扰驱动方法较优，但该方法对齿槽力矩峰值的敏感程度略大于闭环减扰驱动方法。当系统中存在一定齿槽力矩峰值误差时，闭环减扰驱动情况下的转速和力矩稳定度略优于开环减扰驱动方法，但两种方法的相对偏差不到10%。

表1 两种驱动方法的减扰效果对比Tab.1 Comparison of disturbance-mitigation effects for these two drive methods

由以上分析可知闭环减扰驱动方法与开环减扰驱动方法在减扰效果和参数误差敏感程度方面差距不大，但在实现难度和系统可靠性方面不及开环减扰驱动方法，因此综合考虑下开环减扰驱动方法更适合电池阵跟踪驱动。图7进一步给出在齿槽力矩峰值偏差±50%范围内，开环减扰驱动下扰动力矩和转速稳定度随齿槽力矩峰值误差的变化关系。在参数误差小于±11%范围内，采用开环减扰驱动方法后的电池阵转速稳定度控制在1%以内，并且扰动力矩稳定度优于1.15%。

图7 参数误差对系统响应的影响Fig.7 Influences of parameter error on system responses

4 结论

(1)步进电机谐波电磁力矩可以近似为电池阵转动规律的比例控制环节，而其齿槽效应是影响驱动过程扰动力矩和转速稳定度的主要因素之一。

(2)根据电池阵跟踪驱动规律的特殊性，从稳态力矩平衡方程出发提出了电池阵闭环和开环输入补偿减扰驱动方法;并且两种减扰驱动策略都能够有效改善电池阵跟踪驱动过程中的速度和力矩稳定度。

(3)在考虑综合多种因素条件下开环减扰驱动方法较优，其在参数误差小于11%范围内可以将转速稳定度控制在1%以内，且力矩稳定度优于1.15%。

［1］ Doherty M J，Tolson R H.Input shaping to reduce solar array structural vibrations［R］.NASA/CR－1998－208698，1998.

［2］Freitas W A.Reduction of structural vibration induced by solar array drive mechanisms using input shaping control techniques［R］.INPE－15302－TDI/1354，2008.

［3］ Miller SE，Kirchman P，Sudey J.Impact of non-uniform solar array stepping on the GOES-N dynamic environment［C］//In.30th Annual AAS Rocky Mountain Guidance and Control Conference，Breckenridge，USA，2007.775 －788.

［4］朱春艳，邵济明，那帅，等.太阳电池翼调姿后残余振动抑制的整形器设计［J］.振动与冲击，2012，31(8):176－180.ZHU Chun-yan，SHAOji-ming，NA Shuai，et al.Design and simulation of input shaper for residual vibration suppression after attitude adjustment of a solar array［J］.Journal of Vibration and Shock，2012，31(8):176－180.

［5］那帅，朱春艳，彭福军，等.基于输入整形技术的太阳翼调姿残余振动抑制实验研究［J］.振动与冲击，2013，32(7):107－112.NA Shuai，ZHU Chun-yan，PENG Fu-jun，et al.Tests for residual vibration suppression of a solar array during attitude control based on input shaping technique［J］.Journal of Vibration and Shock，2013，32(7):107－112.

［6］赵江涛，李果.挠性高稳定度卫星载荷扰动力矩补偿研究［J］.空间控制技术与应用，2011，37(4):7－12.ZHAO Jiang-tao，LI Guo.Torque compensation for payload disturbance of a flexible satellite with high stability［J］.Aerospace Control and Application，2011，37(4):7－12.

［7］张猛，祝晓丽，陆娇娣，等.一种高稳定度太阳帆板驱动机构控制方法［J］.空间控制技术与应用，2010，36(4):46－49.ZHANG Meng，ZHU Xiao-li，LU Jiao-di，et al.A high stablity control method for solar array drive mechanism ［J］.Aerospace Control and Application，2010，36(4):46－49.

［8］陆栋宁，刘一武.挠性太阳帆板驱动控制系统研究［J］.空间控制技术与应用，2013，39(1):27－33.LU Dong-ning，LIU Yi-wu.On the control of flexible solar array drive systems［J］.Aerospace Control and Application，2013，39(1):27－33.

［9］朱仕尧，谢燕，雷勇军.太阳能电池阵跟踪驱动过程扰动特性分析［J］.国防科技大学学报，2014，36(1):27－33.ZHU Shi-yao，XIE Yan，LEI Yong-jun.Characteristic analysis of disturbance aroused by solar array tracking drive ［J］.Journal of National University of Defense Technology，2014，36(1):27－33.

［10］ Takemura H，Hirabayashi H，Ohmori N，et al.Vibration suppression of stepping motor driven systems using cogging torque compensator［J］.Japan Society of Mechanical Engineers，2012，78(785):74 －81.

［11］Le Q N，Jeon J W.An improved method of speed damping for a stepper motor with a smooth speed estimation［C］//In.International Conference on Robotics and Biomimetics，Bangkok，Thailand，:IEEE，2008.1438 －1443.

［12］ Islam R，Husain I，Fardoun A，et al.Permanent-magnet synchronous motor magnet designs with skewing for torque ripple and cogging torque reduction［J］.IEEE Transactions on Industry Applications，2009，45(1):152 －160.