几何非线性空间梁的动力学建模与实验研究

徐 圣，刘锦阳，余征跃

(上海交通大学 船舶海洋与建筑工程学院，上海 200240)

由多个柔性部件组成的多体系统称为柔性多体系统，如大型空间展开机构、风力发电机叶片、直升飞机机翼等。在外载荷作用下，每个柔性部件可能会产生较大的弹性变形。梁被定义为某一方向上的尺寸比另外两个方向大得多的构件，目前对大变形空间柔性梁的建模和分析因为几何非线性的存在而变得具有挑战性，在保证计算精度的前提下，如何提高数值计算的收敛性，实现大变形空间柔性梁系统高效的动力学仿真是一个非常有意义的命题。

混合坐标法［1］采用刚体大范围运动的刚体坐标与柔性体的节点坐标(或模态坐标)为广义坐标，建立柔性多体系统刚－柔耦合的动力学模型。传统的混合坐标法在建模过程中，直接套用了以线性小位移为基本前提的结构动力学假设，忽略了应变和位移关系式中弹性变形的高次项，并采用模态缩减法提高计算效率。然而，在大变形情况下，线弹性理论和模态缩减法均失效，需要考虑几何非线性项，混合坐标法的优势就无法体现。

绝对节点坐标法［2－4］是目前应用较为广泛的大变形柔性多体系统动力学建模方法。该方法的特点是选取柔性梁各单元节点相对惯性基的位移和斜率作为广义坐标，建立动力学方程。这样就不需要引入大范围运动变量和变量位移坐标，广义坐标全部是全局坐标，得到的质量阵为常数阵。Omar等［5］进一步考虑剪切效应，建立二维梁的有限元模型。在平面梁的基础上，Shabana等［6］将绝对节点坐标法推广到大变形的空间梁。但是，由于取每个节点的绝对位移坐标和沿局部坐标系三个方向的斜率坐标为广义坐标，空间梁的每个节点有12个自由度，计算量较大，收敛速度缓慢。虽然考虑了横向剪切和截面变形，但是弯曲问题的数值收敛性低于预期，存在着剪切锁定［7－8］问题。

解决大变形问题的另一种方法是几何精确建模方法［9］，该方法将空间中轴线的三个方向的位移和横截面的三个方向的转角作为广义坐标，建立动力学方程，但是在对三个横截面转角进行有限元离散时，如果用线性插值函数表示有限转角，容易引起数值计算误差。为了解决这个问题，需要对后一个节点相对前一个节点的转角坐标进行线性插值，使建模过程复杂化。由于工程中常见的空间梁的厚度和宽度的比值很小，横向剪切可以不计，中轴线的切线和横截面法线基本垂直，只需要考虑拉伸变形，弯曲变形和扭转变形，这样，除了扭转角，其余转角均可用绝对位移关于局部坐标的偏导数表示，从而避免了用线性插值函数对有限转角进行插值引起的精度问题。

和兴锁等［10］考虑梁的纵向、横向、侧向弯曲变形以及扭转变形的耦合项，利用Lagrange方程建立具有大范围运动和非线性变形的柔性梁的有限元动力学方程。陈思佳等［11］在动力学方程中保留与非线性耦合量相关的某些高阶项，建立了做大范围旋转运动的中心刚体－柔性悬臂梁系统的高次刚柔耦合动力学模型。目前，现有大型工程软件LS-DYNA，ABAQUS等均可以用于计算大变形问题，但是由于这些软件在动力学建模时，为了简化公式，对方向余弦阵作了近似，需要取较多的单元才能保证收敛和计算精度。

为了准确而高效地解决大变形空间梁的动力学问题，本文基于几何精确建模方法建立了大变形细长空间梁的几何非线性动力学模型，并通过动力学实验验证建模理论的正确性，通过与LS-DYNA的数值对比验证了本文方法的快速收敛性。首先用空间曲梁中线上任意一点的3个绝对位置坐标和横截面的3个姿态角描述横截面的位置和姿态，详细推导了应变和曲率和位置、姿态坐标的关系，在此基础上基于中线切线与横截面法线重合的假设，不计横向剪切变形，将节点广义坐标数从6个减少为4个，简化了动力学模型，从而减小了数值仿真所需的计算时间。在大变形情况下，设计气浮台和柔性空间梁系统的刚－柔耦合动力学实验平台，通过对气浮台和梁系统的刚－柔耦合实验验证了本文的几何非线性空间梁动力学模型的准确性。此外，就同一算例，分别用几何非线性空间梁建模方法和现有大型工程软件(LS-DYNA)进行仿真计算，获得一致的结果。进一步将本文方法仿真计算所需的时间与LS-DYNA进行比较，验证了本文方法具有良好的单元收敛性和高效性。本文方法的特点在于利用较少的梁单元即可获得足够高的计算精度，可有效减少计算耗时。

1 应变和曲率的推导

作大范围运动的空间柔性曲梁如图1所示。建立三个相关的空间坐标系:O－e1e2e3为固定的参考坐标系，P－为固结于变形前过梁中轴线上P点的横截面坐标系，P'－为固结于变形后过梁中轴线上P'点的横截面坐标系。弧线坐标s为曲梁根部至中轴线参考点的弧长的长度。变形前横截面上任意一点的坐标阵为:

图1 变形前后的空间曲梁Fig.1 A spatial curved beam before and after deformation

不计横截面的翘曲变形，并假定横截面的中心在中轴线上，变形后横截面上任意一点的坐标阵为:

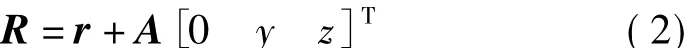
式中，y，z是横截面上任意一点相对中轴线参考点的截面坐标，r0，r分别是中轴线上P点变形前后在固定参考坐标系下的坐标阵，r0=［r01r02r03］T，r=［r1r2r3］T，A0，A 分别是变形前后横截面坐标系相对参考坐标的方向余弦阵。

设横截面上任意一点的坐标阵对自然坐标s求导用‘表示，根据几何精确梁理论，梁上任意一点处的应变列阵为:

式中，ε1表示轴向拉伸应变，ε2，ε3表示横向剪切变形。将式(1)和(2)代入式(3)，得到:

进一步改写得到:

为简化表达，令

为提高几何非线性空间梁的计算效率，考虑减小整个广义坐标阵的规模。对于细长梁来说，其横向剪切应变可以忽略。假定曲梁中轴线的切向与横截面法向一致，则有:

中轴线上对应点的应变列阵可简化为

利用关系式(12)得到:

由于2和3可以用r和r'表示，横截面的位置和姿态可以用r，r'和1描述，从而缩减了节点自由度。将式(15)～(17)代入式(9)，得到:

2 柔性梁的有限元动力学方程

下面采用2节点Hermite函数对每个梁单元进行插值。设第i个梁单元坐标阵qi，总体广义坐标阵q，Bi为单元坐标阵qi与总体坐标阵q之间的转换阵，qi=Biq，则

将式(23)和(24)代入式(14)，弹性力的虚功率为:

设FP是作用于中轴线上P点的外力在O－e1e2e3上的坐标阵，外力的虚功率为:

将式(37)和(38)代入(36)，外力偶的虚功率为:

其中，Φq为约束方程关于q的导数阵，λ为与约束力(偶)相关的拉格朗日列阵。方程(41)需要与运动学约束方程联合求解。

3 数值仿真与讨论

3.1 大变形悬臂梁动力学响应研究

不计重力，考虑一端悬臂的细长柔性直梁。A、B分别是梁的左端点和右端点，在梁右端点B处施加沿着z轴正向的外力偶M，悬臂梁做大范围运动，如图2所示。

图2 力偶作用下的柔性悬臂梁Fig.2 A flexible cantilevered beam applied with tip torque

梁的长度为1 m，横截面为边长2 mm×2 mm的正方形。梁的材料参数为:ρ=2 700 kg/m3，E=7×1010Pa，μ =0.3。

外力偶M的大小随时间的变化规律为:

在本文的几何非线性建模基础上，用广义－α方法(谱半径取0.5)对动力学方程进行数值求解，同时利用LS-DYNA对该悬臂梁进行动力学仿真，得到梁的右端点y方向的位移和速度随时间(1～10 s)的变化曲线，如图3和图4所示。可以看出，本文方法与LS-DYNA的计算结果吻合。

图3 梁端点的y方向位移Fig.3 Tip displacement of the tip point in y direction

图4 梁端点的y方向速度Fig.4 Tip velocity of the tip point in y direction

表1为本文方法和LS-DYNA的仿真耗时比较。可以看出，本文方法使用10个梁单元(最少收敛单元数)，计算时间为42 s;LS-DYNA使用45个梁单元(最少收敛单元数)，计算时间为200 s。可见，几何非线性方法在保证小误差的同时，由于10个梁单元就可以收敛，具有更高的计算效率。

表1 本文方法与LS-DYNA的仿真耗时对比Tab.1 Comparison of time cost of the present formulation and LS-DYNA

3.2 柔性梁的刚－柔耦合动力学研究

如图5所示，气浮台B1绕z轴作定轴转动，矩形柔性梁B2固结在气浮台上。xyz为固结于地面的惯性基，x1y1z1为气浮台连体基，x2y2z2为柔性梁浮动基。梁的浮动基的z2方向与气浮台的转轴z1的夹角为a=π/4，重力沿着 z1的负向。梁长1.45 m，宽0.1 m，厚0.002 5 m，体密度 2 766 kg/m3，弹性模量 6.9 × 1010Pa。气浮台的转轴与梁的内端点的距离为0.35 m，气浮台的转动惯量为J=9.557 kg·m2，观测点C和D到A点的距离分别为0.3 m和1.2 m 。

图5 气浮台刚－柔耦合实验平台Fig.5 Air-floating rigid-flexible coupling experiment test bed

以q—=［θqT］T为系统广义坐标，q为梁上各节点的广义坐标阵。由于 B2在A点与B1固结，且两物体连体基中向量x1与向量x2平行，因此，y1和z1均垂直于x2。y1与y2之间的夹角为a=π/4，z1与y2之间的夹角为a+π/2=3π/4，则系统的运动学约束方程为:

其中，A(θ)为气浮台连体基x1y1z1关于惯性基xyz的方向余弦阵。

初始时刻，矩形梁无变形地搁置在倾斜α=45°的平板上，释放后柔性梁在重力作用下产生弹性变形，气浮台同时发生转动。

用本文几何非线性空间梁理论对上述系统进行建模仿真，并通过实验测试系统响应。在仿真计算中，考虑了结构阻尼力，阻尼阵C=βM(根据振幅衰减率得到阻尼系数β为0.2)。通过角速度传感器测得气浮台的角速度以及观测点C和D的上表面的纵向应变随时间的变化曲线，将测得的实验数据与仿真结果进行对比，如图6图7和图8所示。

图6 转台的角速度Fig.6 Angular velocity of the hub

图7 C点上表面的轴向应变Fig.7 Axial strain of point C on the upper surface

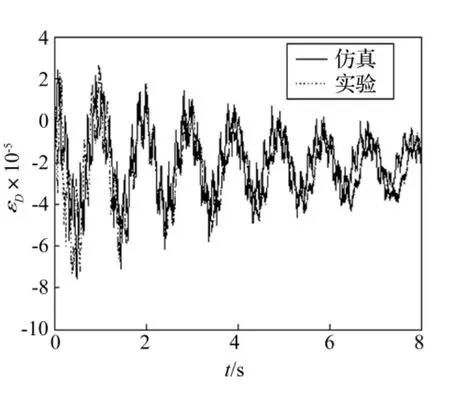
图8 D点上表面的轴向应变Fig.8 Axial strain of point D on the upper surface

由上述曲线图可以看出，几何非线性方法计算所得的气浮台角速度，以及观测点C和D上表面的轴向应变与实验测量值基本吻合。实验值的频率略微低于计算值，这是由于空间梁与气浮台的固结不是理想刚体约束，在实验中有微小变形。通过数值对比，验证了本文几何非线性方法的准确性。

4 结论

(1)与LS-DYNA相比，本文几何非线性空间梁建模方法在保证误差较的同时具有较高的计算效率。首先，该方法将每个节点的坐标数降为4个，从而缩减了梁的整体广义坐标规模。其次，数值解收敛所需要的单元数少于LS-DYNA，有利于减小计算量。因此，几何非线性空间梁建模方法在计算效率上具有优越性。

(2)设计了气浮台－空间梁系统刚－柔耦合动力学实验平台，通过动力学仿真结果与实验值的比较，验证了本文几何非线性空间梁建模方法的准确性。

［1］Linkins P W.Finite element appendage equations for hybrid coordinate dynamic analysis［J］.International Journal of Solids＆ Structures，1972，8(5):709－731.

［2］ Shabana A A，Schwertassek R.Equivalance of the floating frame of reference approach and finite element formulations［J］，International Journal of Non-Linear Mechanics，1998，33(3):417－432.

［3］ Shabana A A，Hussein H A，Escalona JL.Application of the absolute nodal coordinate formulation to large rotation and large deformation problems ［J］， ASME Journal of Mechanical Design，1998，120(2):188－195.

［4］Berzeri M，Shabana A A.Development of simple models for the elastic forces in the absolute nodal coordinate formulation［J］.Journal of Sound and Vibration，2000，235(4):539－565.

［5］Omar M Z，Shabana A A.A two-dimensional shear deformable beam for large rotation and deformation problems ［J］.Journal of Sound and Vibration，2001，243(3):565－576.

［6］Shabana A A，Yakoub R Y.Three dimensional absolute nodal coordinate formulation for beam elements:theory［J］.ASME Journal of Mechanical Design，2001，123(4):606－613.

［7］Gerstmayr J，Shabana A A.Analysis of thin beams and cables using the absolute nodal coordinate formulation ［J］.Nonlinear Dynamics，2006，45(1－2):109－130.

［8］ Schwab A L，Meijaard J P.Comparison of three-dimensional flexible beam elements for dynamic analysis:Finite element method and absolute nodal coordinate formulation ［J］，ASME Journal of Computational Nonlinear Dynamics，2005，5(1):1－10.

［9］Bauchau O A.Flexible multibody dynamics［M］.Dodrecht:Springer，2011.

［10］和兴锁，邓峰岩，吴根勇，等.对于具有大范围运动和非线性变形的柔性梁的有限元动力学建模［J］.物理学报，2010，59(1):25－29.HE Xing-suo， DENG Feng-yan， WU Gen-yong， et al.Dynamic modeling of a flexible beam with large overall motion and nonlinear deformation using the finite element method［J］.Acta Physica Sinica，2010，59(1):25 －29.

［11］陈思佳，章定国，洪嘉振.大变形旋转柔性梁的一种高次刚－柔耦合动力学模型［J］.力学学报，2012，45(2):251－256.CHEN Si-jia，ZHANG Ding-guo，HONG Jia-zhen.A highorder rigid-flexible coupling model of a rotating flexible beam under large deformation［J］.Chinese Journal of Theoretical and Applied Mechanics，2012，45(2):251 －256.