岩石动态劈裂试验的最优试件尺寸分析

方新宇，许金余，2，刘 石，陈腾飞，王 鹏

(1.空军工程大学 机场建筑工程系，西安 710038;2.西北工业大学 力学与土木建筑学院，西安 710072)

岩石的抗拉强度往往只有其抗压强度的1/8～1/10，这使得拉伸破坏成为岩体失稳破坏的主要方式。而工程中常见的岩石结构稳定性、可靠性等问题都涉及到岩石的动态强度，因此高应变率加载下岩石的动态拉伸力学特性已成为岩石力学与工程界的热门课题［1］。Carneiro等［2］首次使用圆盘试件进行静态劈裂抗拉试验，从此诞生了岩石力学中著名的巴西圆盘法。王启智等［3］从试件尺寸上对巴西圆盘进行了改进，提出平台巴西圆盘法，以解决常规巴西圆盘在加载端易出现应力集中的问题，保证了中心起裂条件的实现。尤明庆等［4］用圆环试件(或称带孔圆盘)分别测定了干燥与饱水状态下的岩石劈裂强度。许金余等［5］采用紫铜波形整形器改进后的SHPB系统进行了三种岩石的平台巴西圆盘动态劈拉试验。

本文采用三维非线性动力分析软件LS-DYNA，建立三维SHPB试验模型，对常规巴西圆盘、平台巴西圆盘和带孔巴西圆盘这三种最常用的劈拉试件，进行岩石动态劈裂试验的数值模拟。并依据模拟试验结果，采用平台巴西圆盘法，对花岗岩试样进行了动态劈裂试验。对比模拟与试验结果，得到了加载应变率与岩石动态抗拉强度的关系，并探讨了用于岩石动态劈裂试验的最优试件尺寸。

1 SHPB试验的数值模型建立

本文所模拟的Ф100 mm SHPB试验装置，主体设备包括:发射装置、发射炮管、射弹、吸能装置、杆件及其调整支架、操控台等［6］。压杆材料为高强合金钢，直径为100 mm，入射杆长4 500 mm，透射杆长2 500 mm，入射子弹长500 mm。试件的直径与厚度分别为100 mm 和 30 mm。弹速等级设为 3 m/s，4 m/s，5 m/s，6 m/s和7 m/s五种，对应的紫铜波形整形器直径依次为22 mm，24 mm，26 mm，28 mm 和30 mm。

子弹、波形整形器，试件与各压杆材料均采用Solid164三维实体单元。压杆材料本构模型为钢材料参数的各向同性线弹性模型，材料参数为:ρ=7 850 kg/m3，E=210 GPa，v=0.3。波形整形器本构模型为T2紫铜的双线性弹塑性模型，材料参数为:ρ=8 900 kg/m3，E=108 GPa，v=0.31。岩石试件采用 HJC(Holmquist-Johnson-Cook)动态损伤本构模型来描述，材料参数取值如表1所示。同时，在 K文件里用*MAT_ADD_EROSION语句添加最大主应变失效准则。

表1 岩石试件的HJC参数Tab.1 The HJC Parameters of rock specimens

采用映射网格划分方法，子弹与入射杆沿径向划分成20份，轴向网格长度控制为0.02 m;波形整形器沿径向划分成8份，轴向由于厚度非常薄(1 mm)，故没有在厚度方向进行划分;三种圆盘试件的网格划分均与压杆相协调。本文将模拟试验分成两步来进行:一是子弹、波形整形器和入射杆的模拟;二是入射杆、试件和透射杆的模拟。其有限元模型的网格划分如图1、图2所示。

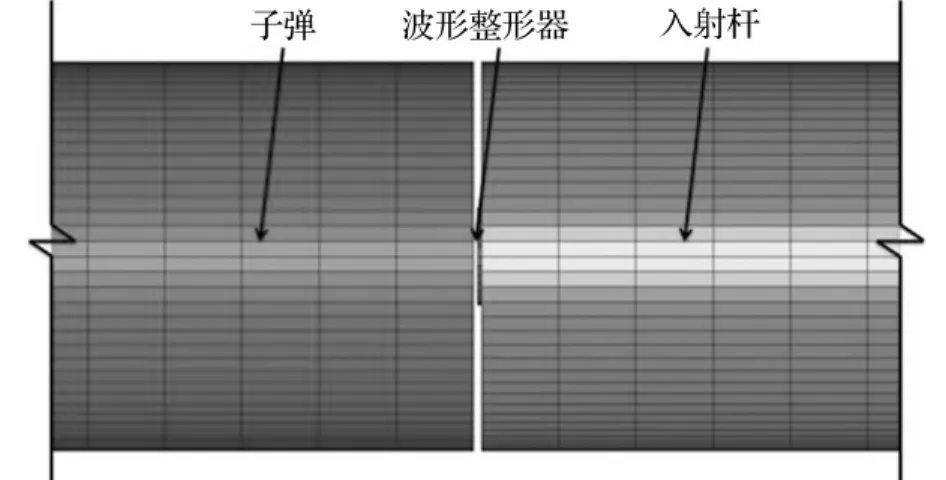
图1 子弹－波形整形器－入射杆有限元模型Fig.1 The finite element model of projectile-pulse shaper－incident bar

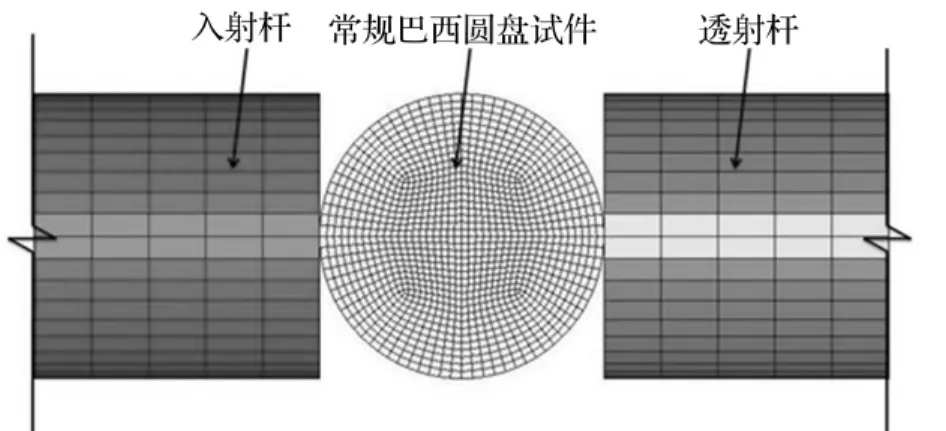
图2 入射杆－试件－透射杆有限元模型(以常规巴西圆盘为例)Fig.2 The finite element model of incident bar-specimen-transmission bar

2 SHPB试验数值模拟的实现

2.1 模拟子弹－波形整形器－入射杆

通过子弹－波形整形器－入射杆的撞击模拟，得到了入射杆杆端经整形后的速度波形曲线。为减小波形振荡的影响，用专业数据分析软件Origin对其进行光滑处理，图3和图4分别为各弹速等级下入射杆端单元加载方向的速度波形曲线以及弹速v=5 m/s时的整形效果。

图3 各弹速等级对应的速度波形曲线Fig.3 Speed waveforms on the end of incident bar(v=3～7 m/s)

由图可知，整形器作用下入射杆端的速度波形由平台波调整为类正弦波，上升延时明显增长，有利于加载过程中实现试件内的应力均匀，速度波形峰值的降低则是由于紫铜整形器发生塑性变形吸收了部分射弹的动能所致;各弹速等级下的速度波形曲线形状相近，均为类正弦波。

图4 弹速v=5 m/s时整形前后的速度波形Fig.4 Speed waveforms on the end of incident bar with/without a shaper(v=5 m/s)

2.2 模拟入射杆－试件－透射杆

将2.1小节模拟得到的五种速度波形曲线加载到入射杆杆端，进行第二步模拟:即入射杆－试件－透射杆的撞击模拟。对试件引入应力均匀性假定，从而可用二波法公式［7］计算平均应变率和平均应变:

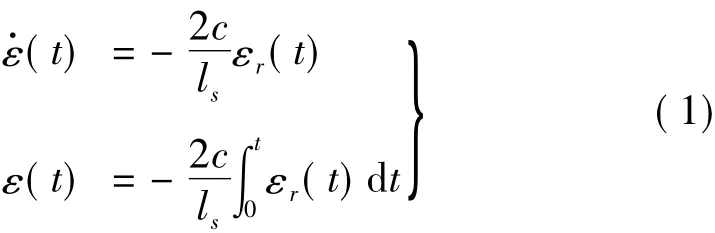
式中，c为压杆的弹性波波速，本文取c=5 172 m/s;ls为试件沿加载方向的长度;εr为测得的反射波。三种巴西圆盘试件的受拉破坏机理相近，但计算其抗拉强度的公式并不相同，在原理上具有继承性，平台巴西圆盘和带孔巴西圆盘的抗拉强度计算公式，都是在常规巴西圆盘的基础上推导出的。

3 常规巴西圆盘法的数值模拟

图5 巴西圆盘受力示意图Fig.5 The stress diagram of Brazilian disc

3.1 原理分析

根据圆盘径向受压的弹性力学解答，并假定岩石试样破坏遵从Griffith强度准则，可推出常规巴西圆盘在准静态加载时的劈裂抗拉强度公式［8］:

式中:P为加载在试件两端的荷载;d=2R，为圆盘直径;h为圆盘厚度，如图5所示。需要注意的是，试样必须满足从中心起裂才能保证该强度公式的有效性［8］。

在此基础上，假定在动载中试样两端达到应力平衡，则可忽略惯性效应;进一步假定试样在达到应力平衡后其内部的应力分布与静载下应力分布类似，则可参照静态巴西盘原理，将试验中测得的试件破坏载荷代入式(2)，计算得到试样的动态抗拉强度式为:

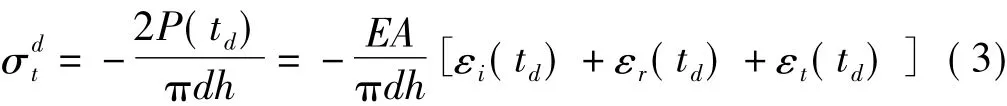
式中:td为试样破坏的时刻;A为压杆的横截面积;εi，εr，εt依次为入射波、反射波和透射波。本文中压杆与试件的直径相同，故可将A=πd2/4代入式(3)，并运用二波法化简整理得:

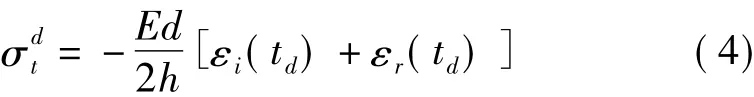
3.2 模拟结果

图7所示为常规巴西圆盘试件在3 m/s，5 m/s和7 m/s这三种弹速下的破坏过程:

观察图6可知，常规巴西圆盘的动态劈拉破坏并不是从中心起裂，而是由加载端起裂。其原因是加载端的应力集中过于严重(理论上说，其接触面实际上是一条交线)。随着加载端的曲面被压碎至平面，出现了一个近似三角形的碎裂区，而后大致从直径末端发展出一条主裂纹，并不断向对径方向延伸。在加载端起裂一小段时间之后，与加载端相对的接触面也开始破坏，并同样向对径方向发展，最终与主裂纹贯通，完成劈裂。随着弹速增加，破坏形态基本相同，但破坏程度加重，次生裂纹的数量也有所增加。

图6 常规巴西圆盘试件破坏过程Fig.6 The failure process of normal Brazilian disc specimens

虽然从破坏过程来看，常规巴西圆盘法并不满足中心起裂条件，但鉴于其为规程［9］中采用的静态劈裂试验方法，故仍用式(4)来估算其动态抗拉强度，并用式(1)计算与各弹速相应的平均加载应变率，得到常规巴西圆盘试件的动态抗拉强度与应变率的关系，如表2所示。

由表2可知，随着应变率增大，常规巴西圆盘试件的动态抗拉强度也增大。

表2 常规巴西圆盘法的与的关系Tab.2 The relation of normal Brazilian disc specimens and

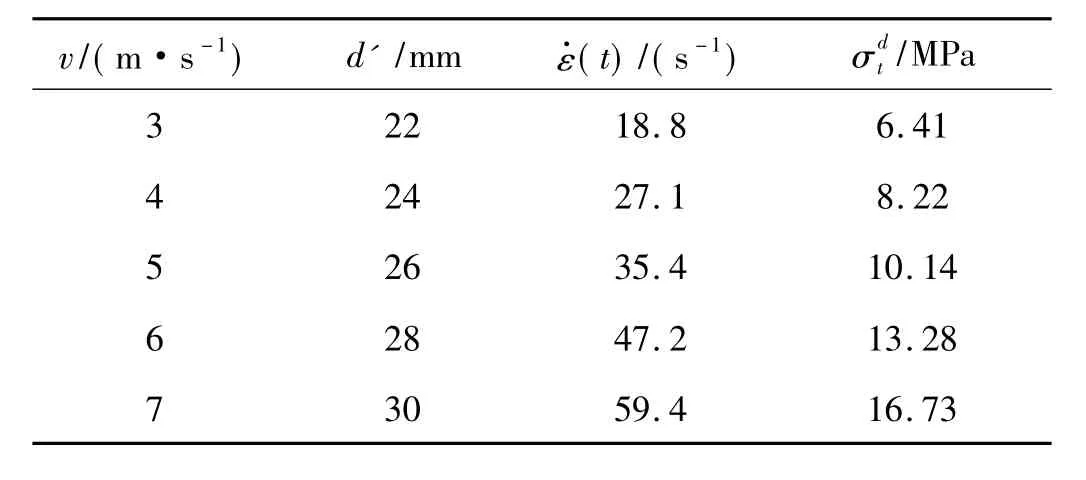
表2 常规巴西圆盘法的与的关系Tab.2 The relation of normal Brazilian disc specimens and

v/(m·s－1)d'/mmε·(t)/(s－1)σdt /MPa 3 22 18.8 6.41 4 24 27.1 8.22 5 26 35.4 10.14 6 28 47.2 13.28 7 30 59.4 16.73

4 平台巴西圆盘法的数值模拟

4.1 原理分析

平台巴西圆盘试件的受力示意图及有限元模型(2α=20°)如图7所示。在巴西圆盘试样中引进平台作为加载面，可以改善加载处的应力状态，避免因应力集中而引起加载端先破坏。根据文献［10－11］的建议，平台中心角在20°～30°之间比较适宜，故本文选取了中心角分别为 20°、22°、24°、26°、28°和 30°的平台巴西圆盘试件进行数值模拟。平台巴西圆盘试件在拉压应力共同作用下破坏的抗拉强度为:

式中:P(td)为破坏时刻加载端面荷载的合力;k为α的函数，可根据有限元计算的圆盘中心点由Griffith准则得到［12］。对应于 2α =20°、22°、24°、26°、28°和 30°的 k值分别为:0.945，0.914，0.898，0.885 和 0.871。

图7 平台巴西圆盘试件受力示意图及有限元模型(2α =20°)Fig.7 The finite element model and stress diagram of flattened Brazilian disc specimens(2α =20°)

4.2 模拟结果

五种中心角的平台巴西圆盘试件在弹速5 m/s打击下的破坏过程如图8所示。观察图8可发现:① 在平台边缘与圆弧过渡处有两个应力集中点，会首先发生破坏，但并不影响试件整体的承载，且在这之后仍然达到了应力均匀状态;② 如忽略平台边缘处的微小破坏，五种中心角的平台试件基本上都在0.94 ms左右满足了中心起裂条件，可见平台加载对于加载端应力集中的缓解是十分明显的;③ 随着中心角的增大，在弹速相同的情况下，试件破坏最显著的特点是贯通两端的裂纹数量由一条增加为两条甚至三条;④ 中心起裂之后，加载端同样发展出近似三角形的碎裂区，同时中心处的主裂纹沿直径不断向两端发展，最终与加载端连通，形成劈裂。通过对破坏形态的分析，推测最适合表1参数的岩石平台巴西圆盘试件的中心角应该在20°～24°之间。

图8 平台巴西圆盘试件在弹速5 m/s打击下的破坏过程Fig.8 The failure process of flattened Brazilian disc specimens(v=5 m/s)

五种平台巴西圆盘试件动态抗拉强度与加载平均应变率的关系如图9所示。

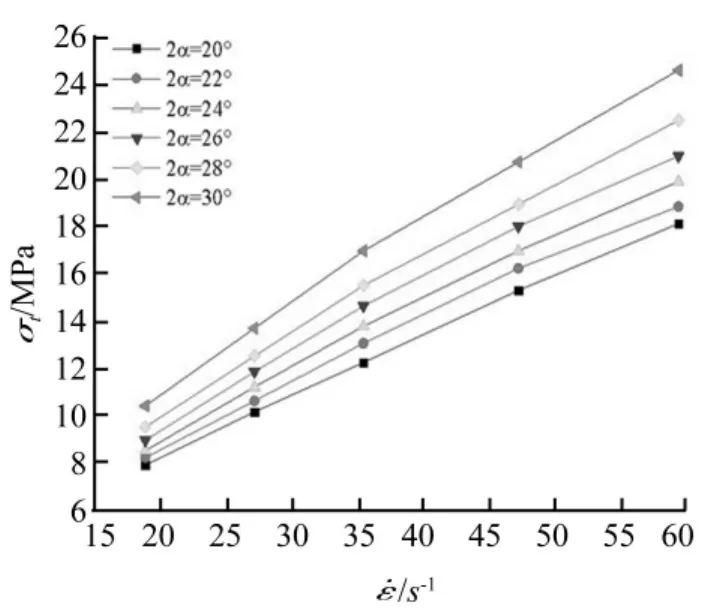
图9 平台巴西圆盘试件和的关系Fig.9 The relation of andof flattened Brazilian disc specimens

由图9可知，随着应变率增大，五种平台巴西圆盘试件的动态抗拉强度都呈增大趋势，并且中心角越大，这种趋势也相应地越明显。而当应变率一定时，中心角越大，平台巴西圆盘试件的动态抗拉强度也越大。这是因为中心角增大，平台承载面也增大，从而使压杆施加的压应力更分散、更均匀，缓解应力集中的同时，也使试件的破坏模式由单纯的拉伸破坏向拉压组合破坏过渡。可以预见，如果中心角进一步增大，也即平台面继续增大，当平台宽度接近圆盘直径时，平台巴西圆盘试件的尺寸会逐渐和抗压试件相似，破坏模式也会由拉压组合破坏过渡到受压破坏。

5 带孔巴西圆盘法的数值模拟

5.1 原理分析

带孔巴西圆盘试件的受力示意图及有限元模型(r/R=0.3)如图10 所示:

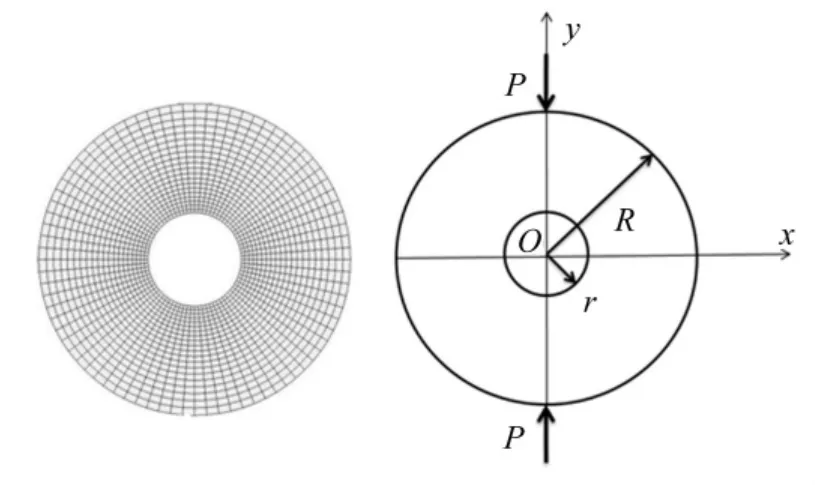
图10 带孔巴西圆盘试件受力示意图及有限元模型(r/R=0.3)Fig.10 The finite element model and stress diagram of holed Brazilian disc specimen(r/R=0.3)

在巴西圆盘试样中心开凿圆孔，是另一种较为常用的实现中心起裂条件的方法。采用文献［13］的建议，根据内孔周边最大拉应力与施加的外部荷载之间的关系，得到带孔巴西圆盘试件的抗拉强度公式为:

式中，Pmax为施加在试样上的峰值载荷，R和r分别为试件的外半径和内半径，h为圆环的厚度。该式是针对静态加载提出的，根据之前的分析，引入应力均匀假定后，动态加载下的公式即:

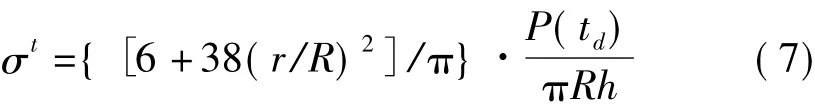
5.2 模拟结果

本文选取了内外孔径比分别为 0.1、0.2、0.3、0.4和0.5的带孔巴西圆盘试件进行数值模拟，这五种试件在弹速5 m/s打击下的破坏过程如图12所示。观察图11可发现:① 虽然中心开孔也会在孔边引起应力集中，但加载端的应力集中现象显然更严重，因此仍然先在加载端出现近似三角形的碎裂区;② 随着内外孔径比的增大，在弹速相同的情况下，试件的破坏程度递增，主要表现在:次裂纹数目逐渐增加，贯通主裂纹的宽度也越来越大;③ 加载端碎裂后，五种内外径比的带孔圆盘试件都在孔边出现若干条裂纹，这些裂纹当中的1～3条逐渐延伸，直至与圆盘边缘贯通，最终形成倒Y形甚至十字形的劈裂破坏。

图11 带孔巴西圆盘试件在弹速5 m/s打击下的破坏过程Fig.11 The failure process of holed Brazilian disc specimens(V=5 m/s)

五种带孔巴西圆盘试件动态抗拉强度与加载平均应变率的关系如图12所示。由图可知，随着应变率增大，五种带孔巴西圆盘试件的动态抗拉强度都呈增大趋势，且孔径比越小，这种增大趋势越明显。而当应变率一定时，内外孔径比越大，带孔巴西圆盘试件的动态抗拉强度也越小;可以预见，当r/R趋近于1时，极限状态的强度值应趋向于0。

图12 巴西圆盘试件和的关系Fig.12 The relation of andof holed Brazilian disc specimens

6 花岗岩动态劈裂试验

6.1 岩样制备

岩样取自秦岭某工程的花岗岩，加工成直径100 mm，高度30 mm的圆柱试件。试件的上下两端面平行度控制在0.05 mm以内。经过陕西国土资源部西安矿产资源监督监测中心检验，花岗岩的矿物成分主要成份如表3所示。比较上述数值模拟中所用的三种巴西圆盘试件，平台巴西圆盘试件显然更为合理。为进一步验证这一点，本文参照文献14的方法［14］，在试件两侧加工中心角分别为20°、25°和30°的平台，平台面的平整度控制在0.02 mm以内。试验共分3 m/s，4 m/s，5 m/s，6 m/s和7 m/s五种弹速等级，与数值模拟相对应。试验设备为Ф100 mm SHPB试验装置，杆件与波形整形器的尺寸、参数等也与数值模拟对象相同。在入射杆与透射杆上粘贴应变片以测试试验中的入射波、反射波和透射波波形。

表3 花岗岩的矿物组成(%)Tab.3 Components of granite(%)

6.2 试验结果

三种中心角的平台巴西圆盘试件在3 m/s，5 m/s和7 m/s这三种弹速打击下的劈裂破坏形态如图13所示。

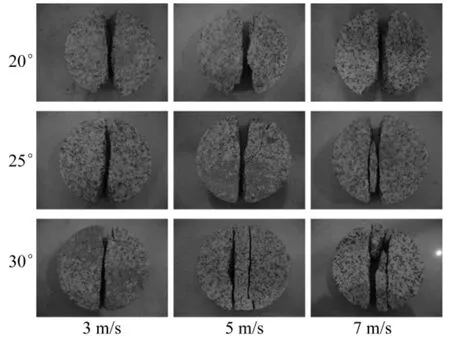
图13 三种平台巴西圆盘试件动态劈裂破坏形态Fig.13 The dynamic splitting failure pattern of 3 kinds of flattened Brazilian disc specimens

对比图8和13发现，试件破坏的模拟结果与试验结果比较吻合，尤其是裂纹数目的变化规律基本一致。三种平台巴西圆盘试件动态抗拉强度与应变率的关系如图14所示。对比图9和14发现，模拟与试验得到的动拉强度－应变率曲线在总体趋势上是相似的，但相对来说，数值模拟得到的曲线波动更大，且强度值更小，曲线位置偏低。

图14 平台巴西圆盘试验中与的关系Fig.14 The relation of andof flatted Brazilian disc tests

7 讨论

与试验相比，数值模拟的优势在于能更方便地观察试件在高应变率加载下的破坏过程，尤其是端面上裂纹的开展过程。比较常规巴西圆盘、平台巴西圆盘和带孔巴西圆盘的数值模拟结果发现:① 从其破坏过程来看，只有平台巴西圆盘试件能较好地满足中心起裂条件，其他两种试件都是先在加载端被压碎;② 随着加载应变率的增大，破坏程度都增大，且动态抗拉强度也增大，但增大趋势逐渐平缓，增长速率越来越小;③ 数值模拟的常规巴西圆盘、中心角20°的平台巴西圆盘和内外孔径比0.4的带孔巴西圆盘以及试验中的中心角20°的平台巴西圆盘，这四种试件的动拉强度与弹速的关系如表4所示，由表4可知，前三者的试验结果十分接近，可以互作参考，但模拟强度值均低于试验强度值。由此推断，如采用带孔巴西圆盘进行岩石动态劈裂试验，试件的内外孔径比取0.4～0.5较为合适。

表4 四种试件的动态抗拉强度与弹速的关系Tab.4 The relation of 4 kinds of specimens’ and V

表4 四种试件的动态抗拉强度与弹速的关系Tab.4 The relation of 4 kinds of specimens’ and V

*表中NBD、FBD、HBD和TFBD分别代表数值模拟的常规巴西圆盘、中心角20°的平台巴西圆盘和内外孔径比为0.4的带孔巴西圆盘以及试验中的中心角20°的平台巴西圆盘。

v/(m·s－1)NBD－σdt/MPa FBD－σdt/MPa HBD－σdt/MPa TFBD－σdt/MPa 3 6.41 7.89 7.7 9.5 4 8.22 10.14 10.26 11.7 5 10.14 12.24 12.72 13.6 6 13.28 15.30 15.34 17.0 7 16.73 18.14 16.9 19.6

此外，还有几点值得注意:① HJC参数的选择会直接影响试验结果的可靠性，本文模拟所用的岩石HJC参数由秦岭某工程花岗岩的单轴压缩试验值计算得到;② 网格划分的优劣会对裂纹发展产生显著影响，本文三种数值模拟试件的网格划分都与压杆协调一致，以避免出现网格畸变，从而保证了模拟结果的可靠性;③ 数值模拟中，破坏的实质是单元满足失效准则后退出工作，这与试验中的破坏是截然不同的。在试验中，试件被压碎后，每一个微元并非像数值模拟中那样消失不见，而是仍然可以起到很小的承载作用，由此聚少成多，就使得数值模拟得出的强度值往往比试验小。

8 结论

通过分析本文三种巴西圆盘试件的数值模拟结果，可得出以下结论:

(1)在岩石SHPB动态劈裂试验中，平台巴西圆盘可以较好地满足中心起裂条件，而常规巴西圆盘和带孔巴西圆盘试件都是先在加载端被压碎，因此平台巴西圆盘法的试验结果可信度更高;

(2)比较五种平台巴西圆盘试件的模拟与试验结果发现:在中心角20°～30°范围内，中心角越接近20°，试件破坏时越易满足中心起裂条件，数值模拟得到的强度值也越接近试验值，因此如采用平台巴西圆盘进行岩石动态劈裂试验，建议试件的中心角取20°～24°;

(3)带孔巴西圆盘虽然不完全满足中心起裂条件，但与常规巴西圆盘试件相比更接近试验值(如表4所示)，因此如采用带孔巴西圆盘进行岩石动态劈裂试验，建议试件的内外孔径比取0.4～0.5;

(4)随着应变率的增大，岩石的动态劈拉强度呈增大趋势，但增大速率越来越小，且这种趋势受到试件尺寸的显著影响:对于平台巴西圆盘试件，中心角越大，试件的应变率效应越明显;而对于带孔巴西圆盘试件，内外孔径比越小，试件的应变率效应越明显。

［1］宋小林，王启智，谢和平.高温后大理岩动态劈裂试样的破坏应变［J］.四川大学学报(工程科学版)，2008，40(1):38－43.SONG Xiao-lin，WANG Qi-zhi，XIE He-ping.Failure strain of Brazilian disc samples of marble under dynamic split tests after high temperature［J］.Journal of Sichuan university(Engineering Sciences Edrtion)，2008，40(1):38 －43.

［2］ Carneiro F，et al.International association of testing and research laboratories for materials and structures［J］.Rilem Bull.1953:1 －20.

［3］王启智，戴峰，贾学明.对“平台圆盘劈裂的理论和试验”一文的回复［J］.岩石力学与工程学报，2004，23(1):175－178.WANG Qi-zhi，DAI Feng，JIA Xue-ming.Reply to the paper‘Split test of flattened rock disk and related theory’［J］.Chinese Journal of Rock Mechanics and Engineering，2004，23(1):175－178.

［4］尤明庆，陈向雷，苏承东.干燥及饱水岩石圆盘和圆环的巴西劈裂强度［J］.岩石力学与工程学报，2011，30(3):464－472.YOU Ming-qing，CHEN Xiang-lei，SU Cheng-dong.Brazilian splitting Strength of discs and rings of rocks［J］.Chinese Journal of Rock Mechanics and Engineering，2011，30(3):464－472.

［5］许金余，刘石，孙蕙香.3种岩石的平台巴西圆盘动态劈裂拉伸试验分析［J］.岩石力学与工程学报，2014，33(增1):2814－2819.XU Jin-yu，LIU Shi，SUN Hui-xiang.Analysis of dynamic split tensile tests of flattened Brazilian disc of three rocks［J］.Chinese Journal of Rock Mechanics and Engineering，2014，33(S1):2814－2819.

［6］刘石，许金余，白二雷，等.高温后大理岩动态劈裂拉伸试验研究［J］.岩土力学，2013，34(12):3500－3504.LIU Shi，XU Jin-yu，BAI Er-lei，et al.Experimental study of dynamic tensile behaviors of marble after high temperature［J］.Rock and Soil Mechanics，2013，34(12):3500－3504.

［7］Kuhn H，Medlin D.SAM Handbook:Vol.8:Mechanical testing and evaluation［M］.Materials Park，OH:ASM International，2000:462 －476.

［8］Muskhelishvili N I.Some basic problems of the mathematical theory of elasticity［M］.Groningen-Holland:P.Noordhoff Ltd，1953.

［9］岩石物理力学性质试验规程，中华人民共和国行业标准编写组.［S］.北京:地质出版社，1994.

［10］尤明庆，苏承东.平台巴西圆盘劈裂和岩石抗拉强度的试验研究［J］.岩石力学与工程学报，2004，23(18):3106－3112.YOU Ming-qing，SU Cheng-dong.Experimental study on splitting test with flattened disk and tensile strength of rock［J］.Chinese Journal of Rock Mechanics and Engineering，2004，23(18):3106－3112.

［11］于庆磊，唐春安，杨天鸿，等.平台中心角对岩石抗拉强度测定影响的数值分析［J］.岩土力学，2008，29(12):3251－3255.YU Qing-lei，TANG Chun-an，YANGTian-hong，et al.Numerical analysis of influence of central angle of flats on tensile strength of granite in split test with flattened disk［J］.Rock and Soil Mechanics，2008，29(12):3251 －3255.

［12］王启智，贾学明.用平台巴西圆盘试样确定脆性岩石的弹性模量、拉伸强度和断裂韧度—第一部分:解析和数值结果［J］.岩石力学与工程学报，2002，21(9):1285－1289.WANG Qi-zhi，JIA Xue-ming.Determination of elastic modulus，tensile strength and fracture toughness of brittle rocks by using flattenedbrazilian disc specimen-Part I:Analytical and numerical results.［J］ Chinese Journal of Rock Mechanics and Engineering，2002，21(9):1285－1289.

［13］Chen C S，PanE，Amadei B.Determination of deformability and tensile strength of anisotropic rocks using Brazilian tests［J］.International Journal of Rock Mechanics and Mining Science，1998，35(1):43－61.

［14］ Wang Q Z，Xing L.Determination of fracture toughness KICby using the flattened Brazilian disk specimen for rock［J］.Engineering Ftacture Mechanics，1999，64(2):193 －201.