欧拉法对方程x'(t)+px(t)+qx(t-τ)=0数值解的振动保持性
2014-09-17刘诗梦高建芳
刘诗梦,高建芳
(哈尔滨师范大学)
0 引言
近几十年来有许多文章是关于延迟微分方程(DDEs)解析解的振动性的研究[1-3].产生这些研究的原因是此类方程在物理学、生物学、生态学及人类某些传染病蔓延等领域内建立的数学模型.有关这些应用的详细内容,可以阅读文献[4-7].
近几年也有一些关于自变量分段连续的延迟微分方程(EPCAs)的数值解的振动性的研究,如文献[8-13].这些文章主要是利用θ-方法和龙格-库塔方法来获得数值解振动的条件.但是目前国内外很少有对纯延迟微分方程的数值解的振动进行的研究.
1 预备知识
考虑延迟微分方程

定义1.1[14]如果x(t)有任意多个零点,则称x(t)是振动的,否则称x(t)为非振动.
定义1.2[14]如果延迟微分方程(1)的所有解都振动,则称方程(1)振动.
定义1.3[14]如果实序列{xn}既不是最终正的也不是最终负的,则称{xn}是振动的,否则称{xn}为非振动.
定理1.4[14]考虑差分方程

那么以下条件等价:
(1)方程(2)的每个解振动;
定理1.5[14]考虑延迟微分方程

那么以下条件等价:
(1)方程(3)的每个解振动;
利用文献[14]中的方法对延迟微分方程(1)做以下等价变换,令

则方程(1)化简为

因此,方程(1)的解x(t)振动等价于方程(4)的解y(t)振动.
引理1.6[14]延迟微分方程(1)的所有解振动的充要条件是,其中a=qepτ.
引理1.7 对x<0,有
证明 构造函数f(x)=(2-x)ex-(2+x),x<0,有
f'(x)=-ex+(2-x)ex-1=ex(1-x)-1令f'(x)=0,得到


即f(x)=(2-x)ex-(2+x)>0,
2 数值解的振动
2.1 显式欧拉法
这一节将研究显式欧拉法即θ=0时的θ-方法.对方程(4)应用显式欧拉方法,得到差分格式,其中是正整数.yn,yn-m分别是y(t)和y(t-τ)在tn处的近似值.
定理2.1 考虑差分方程
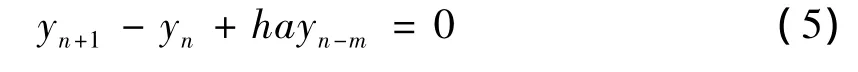

证明 方程(5)所对应的特征方程为

由定理1.4知,差分方程(5)的每个解振动等价于其对应的特征方程(6)没有正根.令

(1)当a<0时,F(0+)=-∞,F(+∞)=+∞,所以F(λ)在(0,+∞)上至少存在一个根λ使F(λ)=0.因此,特征方程(6)有正根,故方程(5)有非振动的解.
(2)当a=0时,λ=1为特征方程(6)的根,故方程(5)也有非振动的解.
(3)当a>0时,显然F(0+)=+∞.
⒈ 当λ≥1时,F(λ)=λ-1+haλ-m>0,所以特征方程(6)在[1,+∞)没有正根.
2.当0<λ<1时,
F(λ)= λ-(1-haλ-m),应用不等式1+x<ex,得到

即 λ-(1-haλ-m)>
因此,F(λ)>0只要考虑

即可.对以上式子的两端取对数,得

令G(λ)=lnλ+haλ-m,有

令G'(λ)=0,则λm=aτ.当λm<aτ时,G'(λ)<0;当 λm>aτ时,G'(λ)>0.
因此,λ =(aτ)m1
是G(λ)在(0,1)上的极小值点,

要求
1+lnaτ>0或lnaτ>-1,
证明完毕.
定义2.2 若延迟微分方程(1)振动,则存在h0>0,当h<h0时方程(5)振动,则称显式欧拉法保持延迟微分方程(1)的振动性.
定理2.3 显式欧拉法无条件保持延迟微分方程(1)的振动性.
2.2 隐式欧拉法
这一节将讨论隐式欧拉法即θ=1时的θ-方法.对方程(4)应用隐式欧拉方法,得到差分格式,其中,正整数m≥2.yn+1,yn+1-m分别是y(t)和y(t-τ)在tn+1处的近似值.将研究与延迟微分方程(1)解析解振动相对应的数值解振动的条件.
定理2.4 考虑差分方程


证明 方程(7)所对应的特征方程为

由定理1.4知,差分方程(7)的每个解振动等价于其对应的特征方程(8)没有正根.令,.

(1)当a<0时,F(0+)=-∞,F(+∞)=+∞,所以F(λ)在(0,+∞)上至少存在一个正根λ,使得F(λ)=0.因此,特征方程(8)有正根,故方程(7)有非振动的解.
(2)当a=0时,λ=1为特征方程(8)的根,故方程(7)也有非振动的解.
(3)当a>0时,显然F(0+)=+∞.
⒈当λ≥1时,F(λ)= λ-1+haλ1-m>0,所以特征方程(8)在[1,+∞)上没有正根,故方程(7)有振动的解.
⒉ 当 0<λ<1时,F(λ)=λ-(1-haλ1-m),应用不等式1+x<ex,得到

即


即可.对以上式子的两端取对数,得

令G(λ)=lnλ+haλ1-m,有

令G'(λ)=0,则 λm-1=(τ-h)a.当 λm-1<(τ-h)a时,G'(λ)<0;当λm-1>(τ-h)a时,G'(λ)>0.因此是G(λ)在(0,1)上的极小值点,


由于整数m≥2,则m-1>0,要求
1+ln(τ-h)a>0或 ln(aτ-ah)>-1,即

则

证明完毕.
定义2.6 若延迟微分方程(1)振动,则存在h0>0,当h<h0时方程(7)振动,则称隐式欧拉法保持延迟微分方程(1)的振动性.
定理2.7 隐式欧拉法保持延迟微分方程(1)的振动性的充分条件是

[1] Bodnar Marek,Piotrowska Monika Joanna,Forys'Urszula.Existence and stability of oscillating solutions for a class of delay differential equations[J].Nonlinear Analysis:Real World Applications,2013,14:1780-1794.
[2] Kubiaczyk I,Saker S.H,Morchalo J.New oscillation criteria for first order nonlinear neutral delay differential equations[J].Applied Mathematics and Computation,2003,142:225-242.
[3] Braverman Elena,Karp Baᶊak.On oscillation of differential and difference equations with non-monotone delays[J].Applied Mathematics and Computation,2011,218:3880-3887.
[4] Yan Jurang,Zhao Aimin,Zhang Quanxin.Oscillation properties of nonlinear impulsive delay differential equations and applications to population models[J].J Math Anal Appl,2006,322:359-370.
[5] Feng Z C,Chicone Carmen.A delay differential equation model for surface acoustic wave sensors[J].Sensors and Ac-tuators A,2003,104:171-178.
[6] Saker S H.Oscillation and global attractivity in hematopoiesis model with delay time.Applied Mathematics and Computation[J].2003,136:241-250.
[7] Bocharov Gennadii A,Rihan Fathalla A.Numerical modelling in biosciences using delay differential equations[J].Journal of Computational and Applied Mathematics,2000,125:183-199.
[8] Liu M.Z,Gao Jianfang,Yang Z W.Oscillation analysis of numerical solution in the θ-methods for equationx'(t)+ax(t)+a1(x([t-1])=0[J].Applied Mathematics and Computation,2007,186:566-578.
[9] Liu M Z,Gao Jianfang,Yang Z W.Preservation of oscillation of the Runge-Kutta method for equationx'(t)+ax(t)+a1(x([t-1])=0[J].Computers and Mathematics with Applications,2009,58:1113-1125.
[10] Gao Jianfang,Song Minghui,Liu Mingzhu.Oscillation A-nalysis of Numerical Solutions for Nonlinear Delay Differential Equations of Population Dynamics[J].Mathematical Modelling and Analysis,2011,16(3):365-375.
[11] Song Minghui,Liu M Z.Numerical stability and oscillation of the Runge-Kutta method for equationx'(t)+ax(t)+a0x(M[(t=N)/M])=0[J].Advances in Difference Equations,2012,146.
[12] Wang Qi,Wen Jiechang,Qiu Shenshan,et al.Numerical oscillation for first-order nonlinear delay differential equations in a hematopiesis model[J].Advances in Difference Equations,2013,163.
[13] Wang Qi,Zhu Qingyong,Liu Mingzhu.Stability and oscillations of numerical solutions for differential equations with piecewise continuous arguments of alternately advanced and retarded type[J].Journal of Computational and Applied Mathematics,2011,235:1542-1552.
[14] GYÖRI I,LADAS G.Oscillation Theory of Delay Differential Equations with Applications[M].Oxford:Academic Press,1991.
