XPPAUT 软件在《常微分方程》教学中的应用

刘宣亮

(华南理工大学数学系，广东广州510640)

1 引 言

在数学课程的教学中，计算机辅助教学起着越来越重要的作用. 人们常用的数学软件有Matlab, Maple 和 Mathematica，这三种软件各有特点，文献 [1]的附录介绍了它们在常微分方程中的应用. 作为求解微分方程的专门的数学软件，XPPAUT (或XPP) 软件使用起来更加方便，功能也更加强大[2]. 该软件是由美国匹兹堡大学 (University of Pittsburgh) 数学系的 Bard Ermentrout 教授于上世纪九十年代所开发，可对微分方程的解进行数值模拟，分支分析，并有动画功能等. 所涉及的微分方程包括：常微分方程，偏微分方程，泛函微分方程，差分方程和随机微分方程. 该软件得到了业界的广泛好评与大量使用, 尽管该软件主要供微分方程的研究者使用，但将软件中的一些功能用于课堂教学，可使常微分方程的一些基本概念和结论的理解更加深入. 特别是使用其中的动画功能，使所考虑的问题生动，形象地显现出来，从而进一步加深对问题的理解.

该软件可在其主页 http:∥www.math.pitt.edu/～bard/xpp/xpp.html 上下载， 按照说明书安装后，即可使用.

2 XPPAUT 软件在教学中的应用

下面根据笔者在《常微分方程》教学中使用XPPAUT软件的几个教学实例来谈谈该软件在教学中的应用. 使用的教材为王高雄等编的《常微分方程》第三版[1]，以下简称“教材”.

① 在讲解“教材”§1.2中的基本概念：“方向场”，“水平等倾斜线”，“垂直等倾斜线”，“奇点”，“轨线”时，有些同学理解不清楚，特别是对“方向场”概念的理解不明白. 下面利用XPPAUT软件对一个二维的微分方程组，作出相应相图来进行讲解，可帮助理解这些概念.

例1考虑“教材”§1.1节例5中的沃特拉(Volterra)被捕食—捕食模型

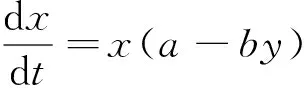
(1)

为了作出其相图，首先编写如下的ODE文件

# the volterra model

x′=x*(a-b*y)

y′=y*(-c+d*x)

par a=0.8, b=0.4, c=0.1, d=0.2

init x=0.5, y=0.5

@ total=50,dt=0.01,nmesh=200

@ xlo=0,ylo=0,xhi=2,yhi=5,xp=x,yp=y

Done

在XPPAUT 软件中运行该文件后，用鼠标点击左侧菜单栏的 Nullcline, 再在出现的下拉菜单中点击 New, 图形中将会出现水平等倾斜线与垂直等倾斜线，如图1所示，实线为水平等倾斜线 (x=0.5)，虚线为垂直等倾斜线 (y=2)，两者的交点为方程组的奇点M. 点击左侧菜单栏的 Dir.field/flow, 然后点击Scaled Dir.Fld, 选取Grid为16，回车后，图形中出现方向场，如图1所示. 将刚才点击左侧菜单栏的Nullcline改为点击左侧菜单栏的Initialconds, 在下拉菜单中点击Mice，然后在图形中点击相平面的不同位置，得到取不同初值的轨线图形，如图2所示，可以看出皆为闭轨线，与向量场的图形相吻合.

图1 方程组(1)的方向场，等倾斜线与奇点

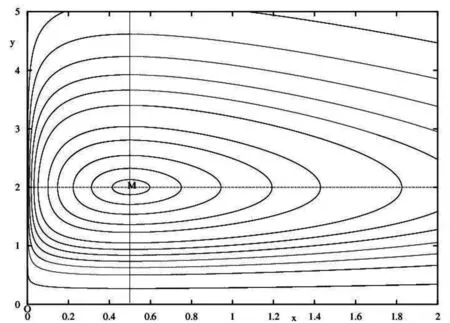
图2 方程组(1)的轨线

② 在“教材”§4.2.4节的质点振动问题中，讨论了四种不同类型的质点的微小振动问题，其振动方程是在φ很小，sinφ用φ近似代替时给出的，如果不作近似代替，则方程的解不能用初等函数表示. 下面我们以有阻尼自由振动为例，在不作近似代替时，来描述如何用XPPAUT软件来画出方程的积分曲线，以及使用XPPAUT软件的动画效果来演示该振动问题，从而对质点振动问题的理解更加生动、具体.

例2考虑有阻尼自由振动方程：

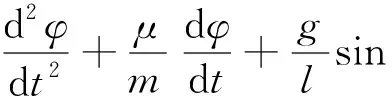
(2)

其中：l=2,g=9.8,m=1,μ=0.4,φ(0)=1,φ′(0)=0.

编写如下ODE文件：pendulum.ode

# the damped pendulum

phi′=v

v′=-(g/l)*sin(phi)-(mu/m)*v

par g=9.8,l=2,m=1,mu=0.4

init phi=1,v=0

@ total=35

done

在XPPAUT软件中运行后，可得图3所示积分曲线

图3 方程(2)的积分曲线

利用XPPAUT 的动画功能，编写动画文件 Pendulum.ani 如下：

# pendulum.ani - goes with pendulum.ode

# animation for the pendulum

#

PERM

# the frame

settext 3;roman;$BLACK

text .2;.9;The pendulum

line .5;.1;.9;.1;$GREEN;2

line .5;.5;.7;.5;$GREEN;2

line .7;.5;.7;.1;$GREEN;2

settext 1;roman;$BLACK

#

TRANS

# the pendulum

vtext .05;.05;t= ;t

line .5;.5;.5+.3*sin(phi);.5-.3*cos(phi);$BLUE;3

fcircle .5+.3*sin(phi);.5-.3*cos(phi);.04;$RED

done

在主窗口中，点击 Viewaxes，然后点击 Toon，出现一个新的窗口(动画窗口)，在此窗口中点击 File，选择动画文件 pendulum.ani，然后点击 Go，你将看到单摆的左右摆动，且摆动幅度越来越小，最后停止在平衡位置.

③ 在“教材”第一章§1.1节例6，作者给出了一个洛伦茨 (Lorenz) 方程的著名例子，该例子表示了由于解对初值的异常敏感而产生混沌(chaos)现象. 在§6.5节中对 Lorenz 方程有进一步的分析，但由于课时限制，通常都不讲§6.5节. 学生往往对解关于初值的异常敏感性不能很好地理解，下面利用 XPPAUT 软件的动画功能，我们可以给出一个直观，形象的解释.

例3在§1.1节中给出的 Lorenz 方程为

(3)

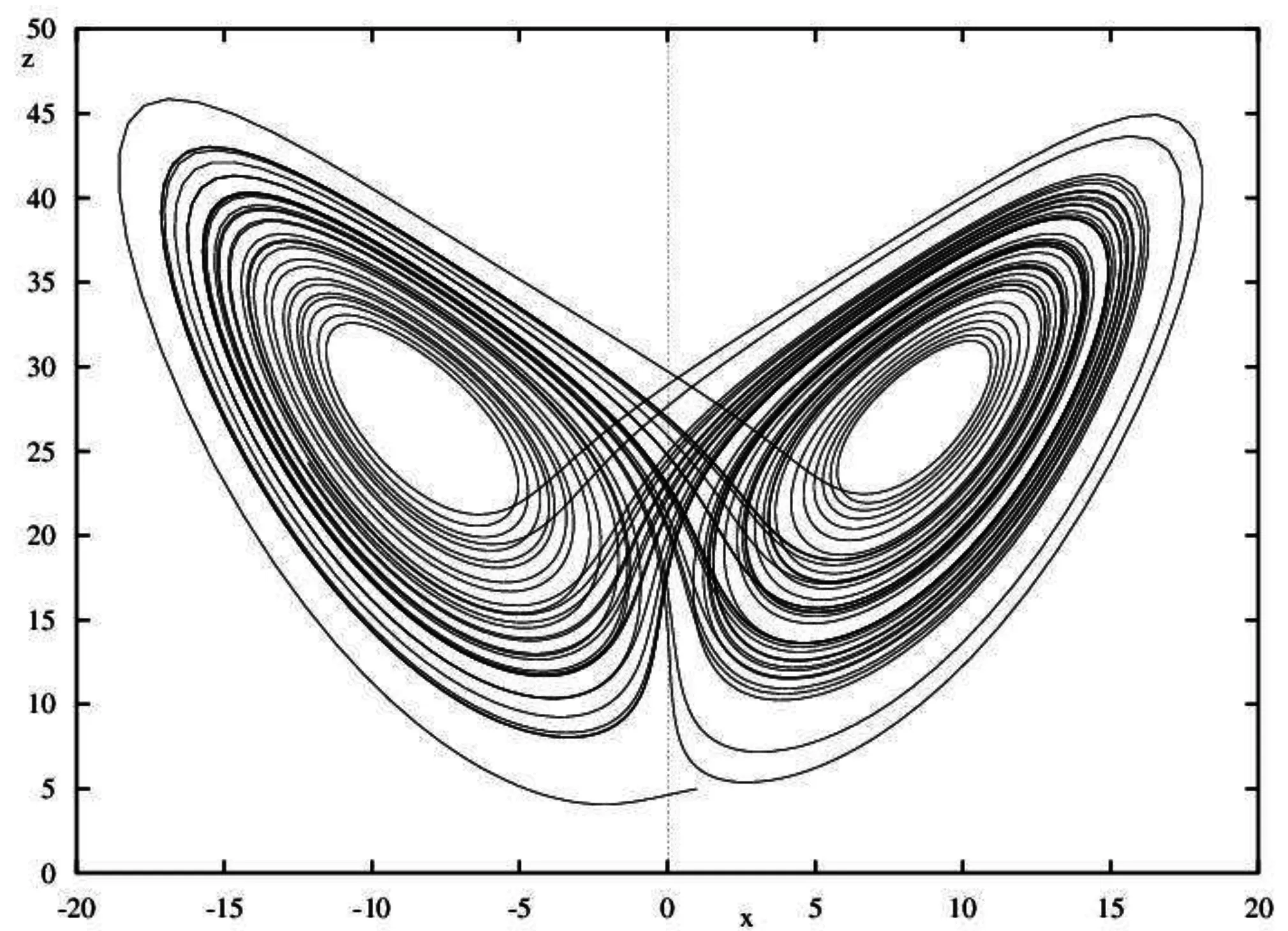
图 4 Lorenz方程的轨线在Oxz平面的投影图

为了说明Lorenz方程关于初值的异常敏感性，我们取60个非常接近的初值，即让它们的x,y坐标相同，z坐标相差很小(相邻的两初值相差不超过0.001)，分别考虑取这60个相差很小的初值时，它们的轨线的变化.

首先，编写如下ODE文件:Lorenz60.ode.

# 60 lorenz equations

x[1..60]’=a*(y[j]-x[j])

y[1..60]’=c*x[j]-y[j]-x[j]*z[j]

z[1..60]’=-b*z[j]+x[j]*y[j]

par c=28,a=10,b=2.66667

init x[1..60]=1,y[j]=-3.6

init z[1..60]=5.00[j]1

@ total=50,dt=.01

Done

此ODE文件描述了60个Lorenz方程分别取60个不同初值时的情形.为了动态地演示取这60个相差很小的初值后的60条轨线的变化情况，我们让60个小球分别位于60个初始位置上，随着时间t的增加，观察它们沿着60条不同轨线在xOz平面的投影的变化情况.为此，编写下面的动画文件：Lorenz.ani

# animation

PERM

line 0;0;1;0;$BLACK;1

line 0;0;0;1;$BLACK;1

line 1;0;1;1;$BLACK;1

line 0;1;1;1;$BLACK;1

TRANS

fcircle (x[1..60]+20)/40;z[j]/50;.02;$BLACK

vtext .05;.05;t= ;t

done

在XPPAUT软件中运行Lorenz60.ode后，点击Viewaxes，再点击Toon，出现动画窗口，点击动画窗口的File，再选择动画文件Lorenz.ani后，然后点击Go，你将看到60个小球随着时间增加慢慢分离开来，相差逐渐增大，最后布满了图4中的整个轨线区域.下面是动画过程中的四帧图：

(1) t=5 (2) t=11

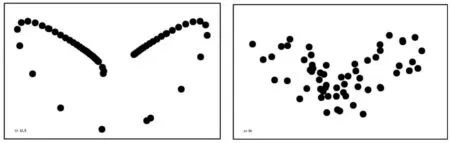
(3) t=12.5 (4) t=50图5 60个小球随时间t变化的四帧图

从图中可以看出，当t=0 时，60个小球几乎重合在一起，当t=11 时，60个小球逐渐分离，当t=12.5 时，60个小球相距拉大，当t=50 时，60个小球布满整个轨线区域，从而看出 Lorenz 方程(3)关于初值的异常敏感性.

3 结束语

在用计算机辅助《常微分方程》的学习时，人们常常使用数学软件对常微分方程的解进行数值计算和绘图，通过直观的几何图形，迅速了解常微分方程解的性态.利用微分方程的专门软件 XPPAUT,不仅可对常微分方程进行数值模拟，作出解的图形，还能利用它的一些特殊功能，如画等倾斜线，方向场等. 将它们运用于教学中，使我们对相应的一些基本概念和内容的理解更加清楚. 特别是使用 XPPAUT 软件的动画功能，可以将方程的解的结果动画演示，这样对所学内容的理解就更加具体和深入，也进一步调动学生对这门课程的学习兴趣.另外，由于常微分方程是与实际联系非常密切的一门学科，像例1-3那样在一些应用例子中来使用 XPPAUT 软件帮助教学，也是非常必要的[3].

[参 考 文 献]

[1] 王高雄,周之铭,朱思铭,王寿松.常微分方程[M].3版.北京：高等教育出版社，2006.

[2] Ermentrout G B. Simulating, analyzing and animatingdynamical systems: a guide to XPPAUT for researchers and students[M]. Philadelphia: SIAM, 2002.

[3] 葛渭高，田玉，廉海荣. 应用常微分方程[M]. 北京: 科学出版社, 2010.