矩阵运算中结果校验的快速判别方法

马德宜， 柳福祥， 尹 玲

(1. 三峡大学理学院，宜昌443002； 2. 广东医学院数学教研室，东莞523808)

1 引 言

线性代数是理工科必修课目之一.虽然线性代数中矩阵运算涉及的方法学生基本上都能掌握，但对结果的正确性却没有把握，计算失误现象比较普遍.最近几年，学生学习线性代数的兴趣与热情有下降趋势.本文结合实际教学经验，认为主要原因是检查过程中大量的重复性加减乘除工作会消耗学生大量的学习时间和精力，并降低了学生的学习兴趣，学生不愿意检查中间计算过程.为了提高学生对矩阵运算结果正确性检验的认识，为了提高学生学习线性代数的兴趣和提高教学质量，本文从矩阵的初等变换[1]、分块矩阵[2]、矩阵的秩[3]、矩阵的逆[4]、合同矩阵[5]和相似矩阵[6]等方面，给出了详细的快速判别方法.

2 矩阵初等变换的快速校验

矩阵的初等变换是线性代数课程的基础，又快又准确的对某个矩阵进行初等变换是基本要求.初等变换的原理比较简单，主要是中学所学的加减乘除混合运算.但数字过于集中，重复工作较多，稍不留神就会导致出错, 因此对矩阵初等变换的结果进行快速验证是必要的.

例1用初等行变换将矩阵

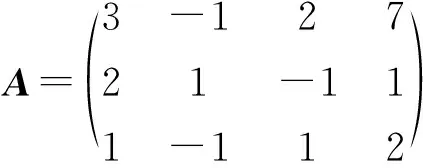
化为行最简形矩阵.

例1到此解答已全部完成.只要初等变换的中间过程没有出错，最简形矩阵一定正确.但如何才能保证中间计算结果没有出错呢？一般而言，自己检查自己中间验算过程是否出错是非常困难的.因此，本文作者结合实际教学经验，总结了一条快速验证最简形矩阵是否正确的方法.即将矩阵A删除最后一列后与矩阵B的最后一列相乘，如果结果等于A的最后一列则正确，否则错误.

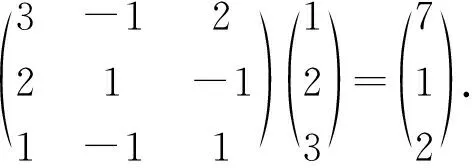
通过计算，相乘结果等于矩阵A的最后一列，故最简形阶梯型矩阵正确的可能性很大.

例3用初等行变换将矩阵

化为行最简形矩阵.

例3到此已经全部解答完成，下面需要进一步验证这个结果是否正确.此时按照例2的方法已经不适用，但实际上只需要将最简形阶梯型矩阵首非零元素1所对应的未知量的值取为最后一列中相对应的值，其它变量取为0即可.

通过验算，矩阵两边相等，可以进一步提高最简形阶梯型矩阵正确性的概率.

3 分块矩阵的快速校验

随着现代科技的发展，社会已进入云数据、大数据时代.由于数据量大，大矩阵的运算也就不可避免.为了对大矩阵高效的计算，分块矩阵提供了一种强有力的手段.但分块矩阵的计算规则很容易与普通矩阵的计算规则相混淆，因此有必要对分块矩阵的计算结果是否正确进行快速验证.

例5给定矩阵

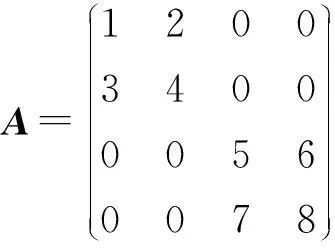
求AB.

解首先将矩阵A,B分块，

我们在实际教学中发现有些学生对分块矩阵的概念没有完全掌握，学生通过计算可以得到一个结果，但他们对分块计算的结果正确性没有把握.为了帮助学生快速增加对结果正确性的信心，作者建议学生对最后每个分块矩阵的结果随机选择一个值，然后用普通矩阵乘法验算，而不需要对每个元素都验算，提高效率，减少重复计算的次数.

例6验证：在B11,B22,E2,O中分别任意选择一个，这里选择中间4个数字进行验证.

(3400)(5300)′=27 (3400)(1043)′=3

(0056)(5300)′=0 (0056)(5300)′=38

通过计算，随机选择的4个数完全正确，故最后通过分块矩阵得出的结果正确性概率非常大.

4 矩阵的秩的快速校验

秩是线性代数中一个较难的概念之一，也是解决许多线性代数问题的关键工具之一.矩阵秩的错误判断，将直接导致线性代数中许多问题无法求解.因此有必要对矩阵的秩进行快速验证.

解对矩阵A进行初等行变换，

由矩阵B，得R(A)=3.

由于中间经过了大量运算，并不能保证中间一点错也没有，需要对此结果进行快速验证.本文总结的快速验证方法是，只需要在矩阵A中找到一个3阶子矩阵行列式不为0，并且随机选择一个4阶子矩阵行列式为0即可，不需要根据秩的定义计算所有4阶子矩阵的行列式，减少校验的时间.

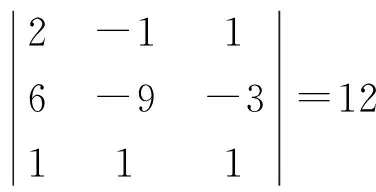
虽然并不能保证此结果完全正确，但它是正确的概率非常大.

5 矩阵的逆的快速校验

逆矩阵的概念，类似于中学所学的倒数，但又有明显区别.逆矩阵在矩阵方程和判断矩阵的某些性质等方面都有着举足轻重的作用.逆矩阵的计算错误，将会影响对矩阵性质的判断，因此有必要对矩阵的逆的结果进行快速验证.

所以

这是求矩阵逆最常用的方法之一.只要中间结果没有错，最后结果一定正确.为了进一步验证此结果是否正确，常用的方法是求AA-1，如果等于E则正确，否则错误.本文作者根据实际教学经验，通过计算det(A)det(A-1)，能更加快速验证其结果是否正确的判断.

例9验证：det(A)det(A-1)=1.

虽然并不能保证此结果完全正确，但它是正确的概率非常大.

6 合同矩阵的快速校验

设矩阵A和B是n阶矩阵.若有可逆矩阵C，使得B=C′AC，则称矩阵A与B合同.若A为对称阵，由矩阵性质则R(A)=R(B).

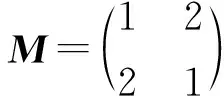
对于这类选择题，需要在最短的时间内给出其正确结果.排除法是一种常用方式.由合同定义，B=C′AC，如果矩阵A,B都可逆，则

det(B)=det(C′)det(A)det(C)=kdet(A),

其中k>0. 换句话说，det(B)与det(A)有相同的正负号.对这四个选项依次计算，

det(A)>0, det(B)>0, det(C)>0, det(D)<0, det(M)<0.

故答案选D.

7 相似矩阵的快速校验

设A,B都是n阶矩阵，如有可逆矩阵P，使得P-1AP=B,则称B是A的相似矩阵.若n阶矩阵A与B相似，则A与B的特征多项式相同.实对称矩阵A与B相似的充要条件A与B具有相同的特征值.

解由A-λE=0，则

由B-λE=0，则

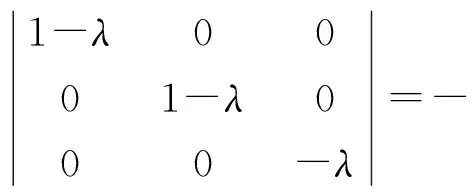
因为A与B的特征值不相同，故A与B不相似.

为了进一步检验中间计算过程是否正确，我们结合实际教学经验，认为只需要将相应的特征值代入行列式计算是否为0即可.

例12验证：当λ=0时，det(A)=det(B)=0.

经过计算，相应的行列式均等于0，进一步说明中间计算错误的概率很小.

8 结 论

矩阵的运算是线性代数中关键的内容之一.对矩阵运算结果是否正确给出快速校验，可以增加其正确性的保证，同时也有助于提高学生的学习效率和学习兴趣.我们结合实际教学经验，对矩阵的初等变换、分块矩阵、矩阵的秩、矩阵的逆、合同矩阵和相似矩阵等方面，分别给出了对其结果正确性的进一步校验方法. 虽然这些方法并不能保证结果百分百正确，但可以快速判断结果是否错误.实际教学效果表明，对矩阵运算结果正确性的再检验，大大提高了学生计算结果的正确率和学习线性代数课程的兴趣.

[参 考 文 献]

[1] 陈汉武,肖芳英.基于初等变换的量子码构造[J].东南大学学报(自然科学版),2011,41(5):934-937.

[2] 李晓彬,刘永辉.Hermitian型分块矩阵的极值秩[J].大学数学,2012,28(1):137-139.

[3] 国慧.矩阵的秩及其应用[J].邢台学院学报,2011,26(2):161-164.

[4] 冯媛.逆矩阵教学与思维能力培养[J].高等数学研究,2013,16(1):113-117.

[5] 朱凤娟,黄永东.关于合同矩阵的一个注记[J].宁夏师范学院学报(自然科学版),2007,28(3):79-80.

[6] 李亦芳,张环理,张丹.相似矩阵的性质及应用[J].河南教育学院学报(自然科学版),2005,14(2):11-12.