高阶常系数非齐次线性微分方程的逆特征算子分解法

郑华盛

(南昌航空大学数学与信息科学学院，江西南昌330063)

1 引 言

目前，直接求n阶常系数非齐次线性微分方程通解的一般方法主要是常数变易法[1]，而大多数情形都是先由待定系数法、算子法、Laplace变换法及分部积分法等[1-6]方法求出非齐次方程的特解，再加上对应齐次方程的通解，由通解的结构而得到非齐次方程的通解.文[7]给出了求其通解的降阶解法.本文提出一种求解任意n阶(n≥2)常系数非齐次线性微分方程通解的逆特征算子分解新方法，该方法只需直接将逆特征算子按有理真分式的因式分解方法分解为一次因式逆算子的形式，问题就转化为求n个一阶非齐次线性微分方程.给出了二阶和三阶常系数非齐次线性微分方程通解的一般公式及特定情形下n阶常系数非齐次线性微分方程的通解公式.本文方法有别于文[2-3]中的算子法，也无须象待定系数法那样限定非齐次项为两种特殊类型.之后，通过几个实例加以验证.

2 主要结论

考虑二阶常系数非齐次线性微分方程

y″+py′+qy=f(x).

(1)

定理1设方程(1)的特征方程L(r)=r2+pr+q=0的根为r1，r2，则

(i) 当r1≠r2∈时，方程(1)的通解为

(ii) 当r1=r2∈时，方程(1)的通解为

(iii) 当r1与r2为共轭复根时，记r1,2=α±iβ(α,β∈，且β≠0)，方程(1)的通解为

y= eαx(C1·cosβx+C2·sinβx)

当r1≠r2∈时，有L(D)=(D-r1I)(D-r2I)，于是方程(1)的解为

(ii) 当r1=r2∈时，有L(D)=(D-r1I)2，于是方程(1)的解为

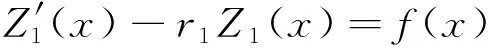
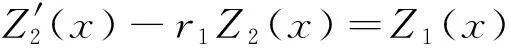
(iii) 当r1,2=α±iβ时，有L(D)=(D-r1I)(D-r2I)，于是由情形(i)可得方程(1)的通解为

类似地，有

定理2设有三阶常系数非齐次线性微分方程

y‴+p1y″+p2y′+p3y=f(x)，

(2)

它的特征方程L(r)=r3+p1r2+p2r+p3=0的根分别为r1，r2，r3，则

(i) 当r1，r2，r3∈且互异时，方程(2)的通解为

(ii) 当r1=r2=r3∈时，方程(2)的通解为

(iii)当r1，r2，r3∈且r1=r2≠r3时，方程(2)的通解为

(iv)当r1∈，时，记r2,3=α±iβ(α,β∈，且β≠0)，方程(2)的通解为

其中Ci(i=1,2,3)为任意常数，且通解表达式中的不定积分均不含任意常数.

一般地，有

定理3设有n阶常系数非齐次线性微分方程

y(n)+p1y(n-1)+p2y(n-2)+…+pn-1y′+pny=f(x)，

(3)

它的特征方程L(r)=rn+p1rn-1+p2rn-2+…pn-1r+pn=0的根为ri(i=1,2,…,n)，则

(i) 当ri∈(i=1,2,…,n)且互异时，方程(3)的通解为

(ii) 当r1=r2=r3=…=rn∈时，方程(3)的通解为

(iii) 除了上述两种情形，特征根的其它情形可能有多种，不便写出通解公式的一般形式，但可类似于情形(i)，(ii)和定理1与定理2，将逆特征算子按有理真分式的因式分解方法化为一阶算子的逆算子形式，然后求多个一阶常系数非齐次线性微分方程的通解即可.

注1 定理1-3给出了求二阶、三阶及n阶常系数非齐次线性微分方程通解的一种新方法.实际求解时，既可以直接利用定理中的公式，也可以不必记公式而按定理的证明过程求解.此外，定理1-3的通解表达式中含有任意常数的部分为对应齐次方程的通解，其余部分为非齐次方程的一个特解.因而利用本文方法也可求高阶常系数非齐次线性微分方程的特解.

3 应用实例

例1[1]求微分方程y″-2y′-3y=3x+1 的通解.

解L(D)=D2-2D-3I=(D+I)(D-3I)，于是原方程的解为

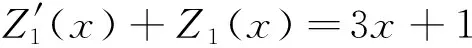
故原方程的通解为

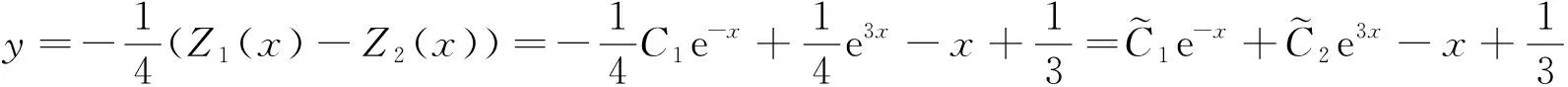
例2[1,7]求微分方程y″-5y′+6y=xe2x的通解.

解由特征方程L(r)=r2-5r+6=(r-2)(r-3)=0，得r1=2，r2=3，于是由定理1得原方程的通解为

解由特征方程L(r)=r2-4r+4=(r-2)2=0，得r1=r2=2，于是由定理1得原方程的通解为

例4[1]求微分方程y″+y=x·cos2x的通解.

解由特征方程L(r)=r2+1=0，得r1,2=±i，于是由定理1中的公式(其中α=0,β=1)得原方程的通解为

例5[4]求微分方程y‴-6y″+11y′-6y=3x的通解.

解由特征方程L(r)=r3-6r2+11r-6=(r-1)(r-2)(r-3)=0，得特征根r1=1，r2=2，r3=3，于是由定理2得原方程的通解为

例6[7]求微分方程y‴-3y″+3y′-y=cosx的通解.

解由特征方程L(r)=r3-3r2+3r-1=(r-1)3=0，得特征根r1=r2=r3=1，于是由定理2得原方程的通解为

例7[ 8]求微分方程y(4)-4y‴+6y″-4y′+y=(x+1)ex的一个特解.

解由特征方程L(r)=r4-4r3+6r2-4r+1=(r-1)4=0，得特征根r1=r2=r3=r4=1，于是由定理3得原方程的一个特解为

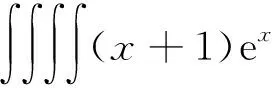
例8[7]求微分方程y(4)+y″=eix的通解.

解L(D)=D4+D2=D2(D-iI)(D+iI).设

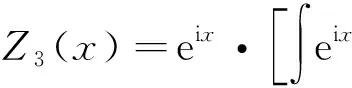
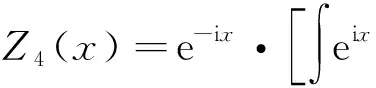
故原方程的通解为

4 结束语

本文提出了一种求任意高阶常系数非齐次线性微分方程通解的逆特征算子分解方法.得到了二阶和三阶常系数非齐次线性微分方程通解的一般公式，及两种特殊情形下n阶(n>3)常系数非齐次线性微分方程通解的公式，具体求解时不需要记公式，而按定理的证明思路求解(如例1及例8).该方法也适用于求任意高阶常系数非齐次线性微分方程的特解. 本文方法思路简单，易于求解，且具有很好的普适性，不失为一种较好的方法.

[参 考 文 献]

[1] 同济大学应用数学系. 高等数学(下册)[M].5版.北京：高等教育出版社，2002：311-315.

[2] 王隽.常系数线性非齐次微分方程的算子解法[J].工科数学，1993,9(4)：204-206.

[3] 阮炯. 差分方程和常微分方程[M].上海：复旦大学出版社，2002：43-90.

[4] 李瑞遐. 应用微分方程[M].上海：华东理工大学出版社，2005：24-31.

[5] 常庚哲，蒋继发. 用分布积分法求解常系数高阶非齐次线性常微分方程[J].大学数学，2003,19(1)：76-79.

[6] 朱德刚.二阶常系数非齐次线性微分方程的特解公式[J].高等数学研究，2010,13(3)：15-16.

[7] 刘林，苏农.n阶常系数非齐次线性微分方程的降阶解法[J].大学数学，2012,28(6)：91-95.

[8] 卢绍莹. 简化待定系数法—求n阶常系数非齐次线性微分方程的一个特解[J].数学的实践与认识，1982(3)：11-13.