减速带激励下汽车的非线性振动特性分析*
2014-09-17吴莹李佳佳农多敏刘少宝
吴莹 李佳佳 农多敏 刘少宝
(1.西安交通大学航天航空学院机械结构强度与振动国家重点实验室,西安 710049)(2.广西柳工机械股份有限公司,柳州 545001)(3.西安理工大学土木建筑工程学院工程力学系,西安 710048)
减速带激励下汽车的非线性振动特性分析*
吴莹1†李佳佳1农多敏2,3刘少宝1
(1.西安交通大学航天航空学院机械结构强度与振动国家重点实验室,西安 710049)(2.广西柳工机械股份有限公司,柳州 545001)(3.西安理工大学土木建筑工程学院工程力学系,西安 710048)
研究了在减速带激励下具有磁流变阻尼器悬架系统汽车的非线性动力学行为.汽车采用七自由度模型,磁流变阻尼器采用Sigmoid模型.根据第二类Lagrange方程建立了汽车振动微分方程,并采用四阶Runge-Kutta法进行了数值仿真.首先以减速带高度为参数对汽车运动进行分岔分析,然后通过时间历程图、相位图、Poincaré截面分析了汽车在不同减速带高度时所呈现的不同运动形式,得到了系统发生混沌运动时减速带的高度范围,并分析了系统经拟周期运动通向混沌运动的途径.研究结果为汽车平顺性控制和安全性设计提供了理论指导.
减速带, 磁流变阻尼器, 非线性, 分岔, 混沌
引言
减速带(speed control hump)是一种强制汽车减速的设施,起着保护车辆安全行驶和遏制交通事故的作用,在学校、收费站、停车厂、高速公路的分岔道、隧道入口等都设置有减速带.由于减速带是凹凸不平的,所以当车辆行驶在减速带上时,会产生大幅度的振动,影响车辆的行驶平顺性和安全性.汽车磁流变悬架是汽车的半主动控制的减震系统,能够控制汽车行驶的平顺性.汽车磁流变悬架是一个具有强非线性的系统,在一定的外界激励条件下极有可能发生混沌运动等复杂的非线性振动[1],从而导致汽车偏离目标,影响汽车行驶的平顺性和安全性,同时还会导致汽车疲劳损坏.因此,研究具有磁流变阻尼器悬架系统汽车的非线性动力学行为具有重要意义.
目前,国内外许多学者多以单自由度1/4汽车模型[2-4]和二自由度 1/4 汽车模型[5-7]为研究对象对汽车的非线性动力学行为进行分析.这些模型比较简单,不能反映车辆整体的运动状态.本文采用七自由度汽车的动力学模型,充分考虑了汽车在运动过程中产生的垂直、俯仰和侧倾运动,更接近实际系统.由于目前还缺乏对高维非线性动力系统中能够引起混沌响应的参数做出具体预测的理论工具,本文对汽车的混沌响应进行了数值分析.
1 七自由度汽车动力学模型
汽车悬架系统采用磁流变阻尼器,模型采用徐赵东[8]等人建立的磁流变阻尼器模型-Sigmoid模型,磁流变阻尼器的阻尼力表示如下:
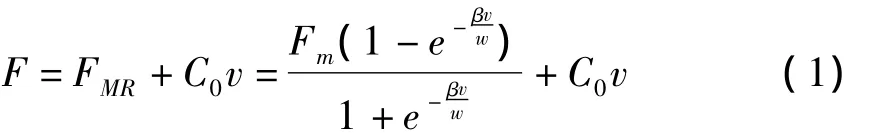
其中Fm为磁流变阻尼器的屈服力,C0为阻尼系数,ω为激励频率,v为相对速度,β为无量纲系数.本文研究的减速带是以连续方式设置在高速公路的分岔道和隧道口上的复合材料型减速带(SCH),如图1所示.这种减速带高度较小,且减振效果好.
复合材料型减速带的凸起高度为h,宽为w,间距为d.当汽车通过复合材料型减速带时,会受到类似矩形波的周期性激励,如图2所示.当汽车以速度v通过一个减速带宽时所需时间为t1=ω/v,通过两个带宽之间的间距所需时间为t2=d/v,则激励周期为T=t1+t2,激励频率可以表示为:

激励函数的矩形波方程可描述为:
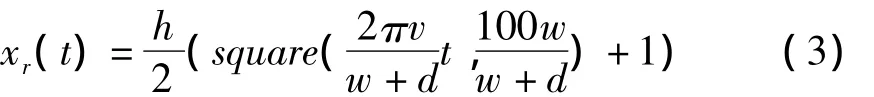
其中square为矩形波函数.

图1 复合材料型减速带[1]Fig.1 The physic photos of composite material SCH[1]
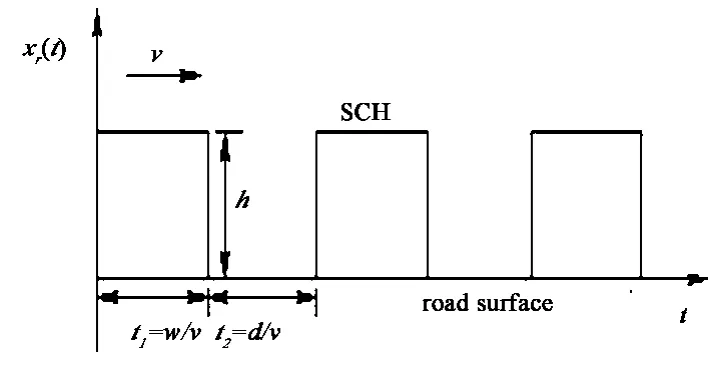
图2 矩形波函数模型Fig.2 The model of rectangular wave
考虑前后轮存在的相位差,路面激励可以描述如下:
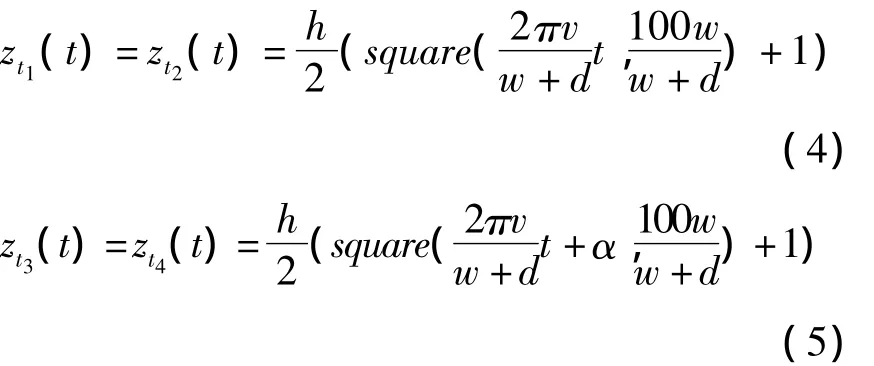
式中zt1、zt2、zt3、zt4分别表示左前轮、右前轮、左后轮、右后轮的激励,α为前后轮的相位差.
七自由度汽车模型如图3所示.车身作为一个刚体,车身具有垂直、俯仰、侧倾三个自由度;前轮独立,可以分别做垂直运动;后轮非独立,可以连后轴质心一起做垂直和侧倾运动.
求出系统的动能、势能、耗散能后,由Lagrange第二类方程可得到系统的振动微分方程如下[7]:
车身的垂直运动微分方程:

车身的侧倾运动微分方程:
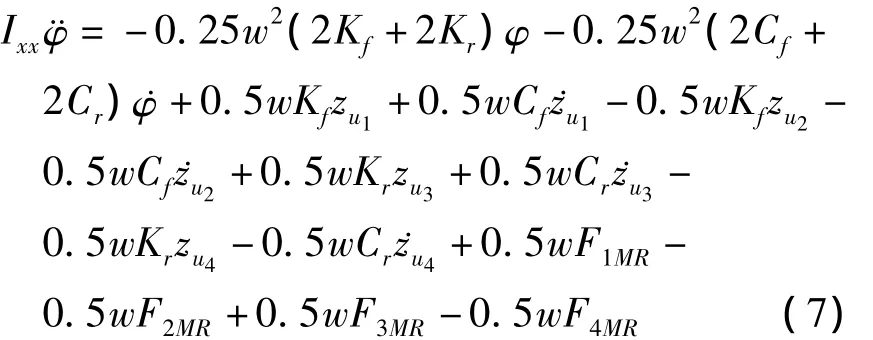
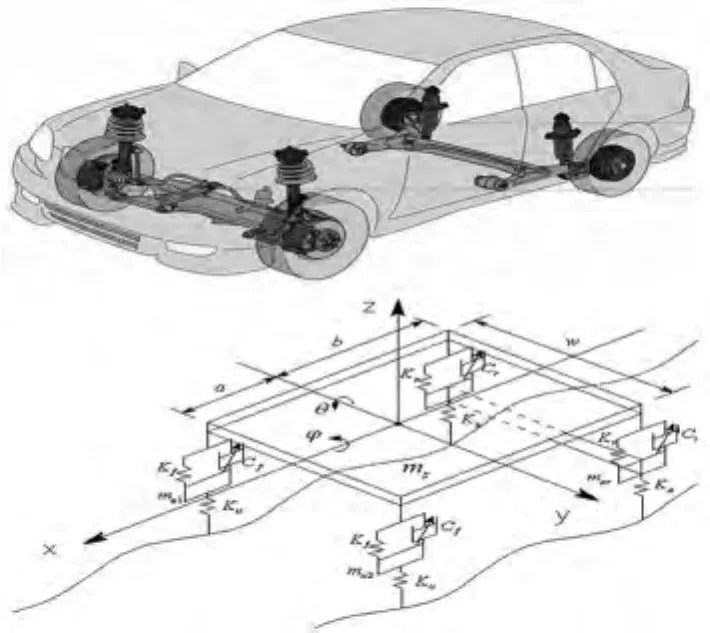
图3 七自由度汽车模型Fig.3 The model of seven-degree-of-freedom car
车身的俯仰运动微分方程:
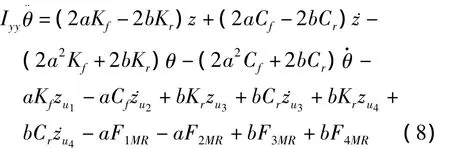
左前轮的垂直运动微分方程:
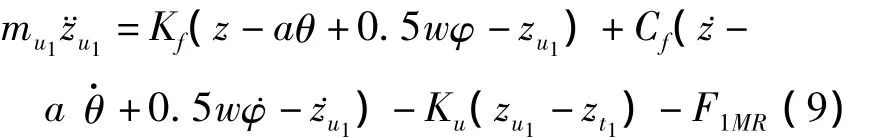
右前轮的垂直运动微分方程:
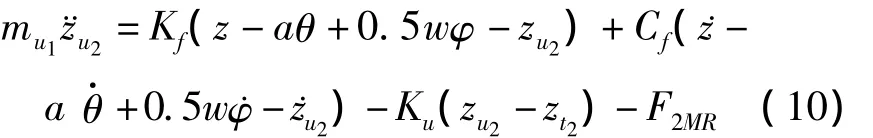
后轮的垂直运动微分方程:
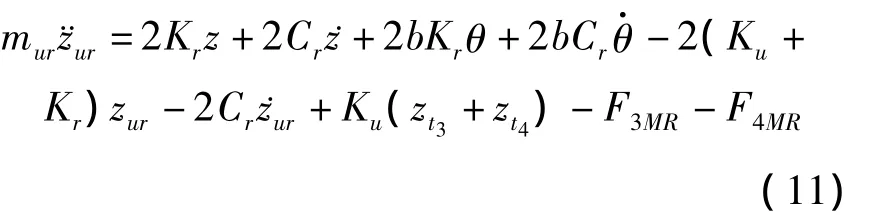
后轮的侧倾运动微分方程:

其中F1MR,F2MR,F3MR,F4MR为磁流变阻尼器的库伦阻尼力,表达式
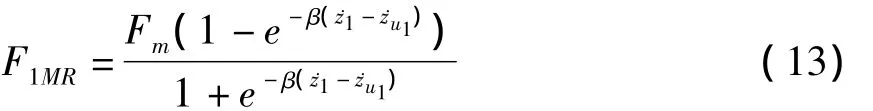

z1,z2,z3,z4表示车身在 4 个车轮处的铅垂直位移.
2 结果与讨论
本文采用四阶Runge-Kutta法进行数值仿真,采用的汽车模型参数[9]如表1所示.
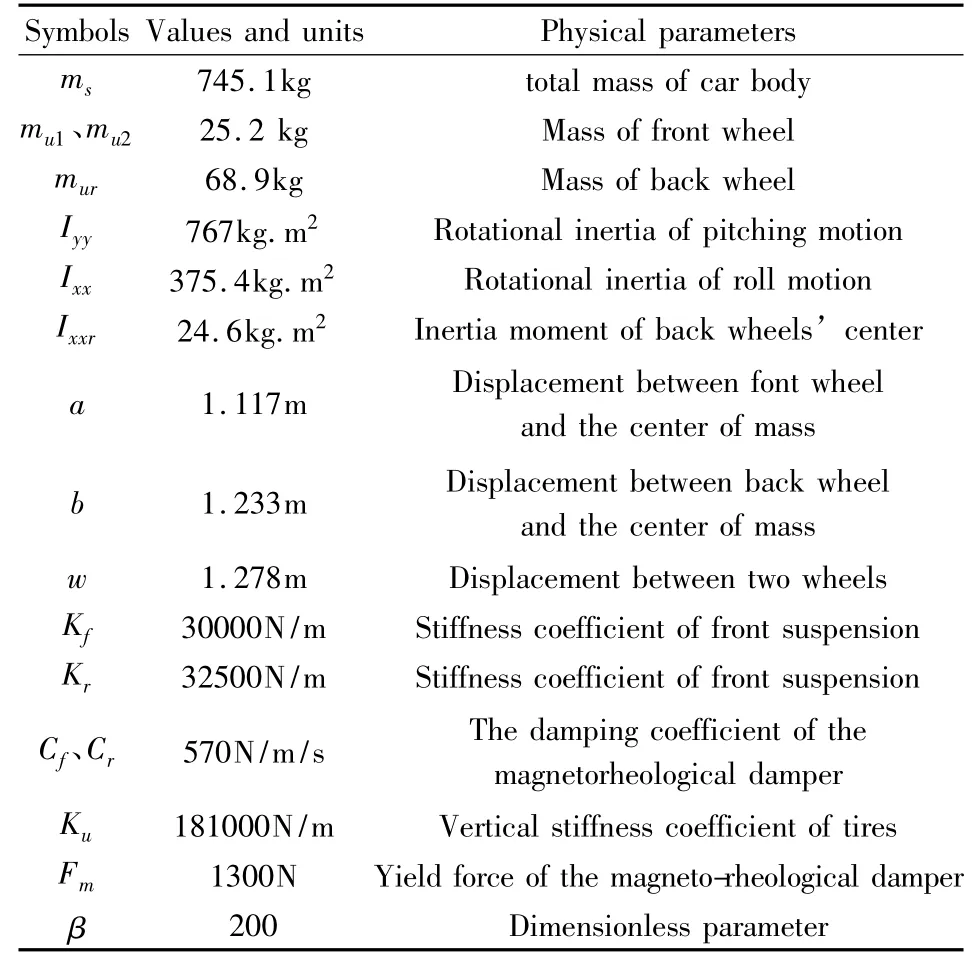
表1 汽车模型的参数Table 1 The parameters for car model
考虑高速公路上设置的减速带高度在0.003m-0.015m 之间,数值分析时 h 的范围取[0.003,0.01],减速带宽度取 w=0.5m,间距取 d=0.5m,前后轮滞后角取α=5π.
由式(2)可知激励频率与汽车行驶速度成正比.为了保证行车的安全,要求汽车通过高速公路上的减速带时速度在40km/h~70km/h之间,数值计算时采用的车速为v=12m/s.以高度h为分岔参数,数值仿真时积分时间为400个周期,为消除瞬态响应的影响,在每一个确定的分岔参数上,用闪频法绘制最后100个Poincaré点,得到的速度分岔图如下:

图4 车身垂直运动位移分岔图Fig.4 Bifurcation diagram of z vs h

图5 车身侧倾运动位移分岔图Fig.5 Bifurcation diagram of φ vs.h
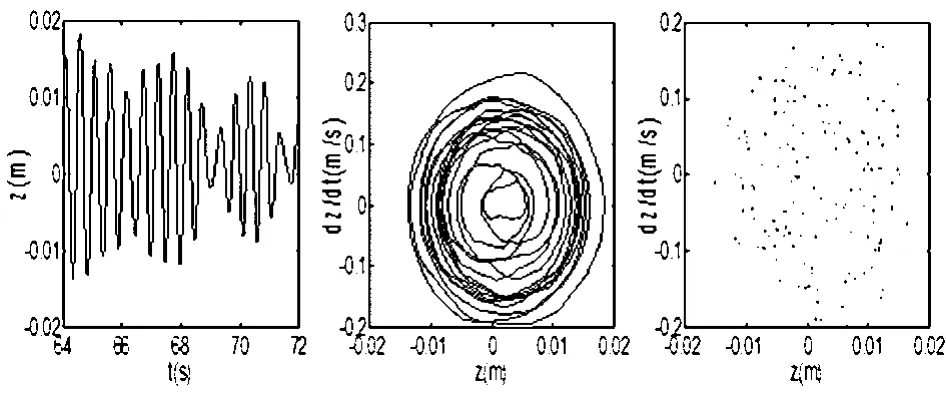
图7 减速带高度h=0.0036m,车身垂直运动时间历程图、相位图、Poincaré截面Fig.7 Time history,phase portrait and Poincaré map of z for h=0.0036m
图4、图5、图6分别是车身的垂直、侧倾、俯仰运动的位移关于复合材料型减速带h高度的分岔图.由以上三个图可以看到,在区间[0.0030,0.0044],车身的垂直、侧倾、俯仰运动非常复杂,具体的运动形式需进一步分析.而在其它区间车身的垂直、侧倾、俯仰运动均为周期运动.下面选取某些特定频率值,利用时间历程图、相位图、Poincaré截面,进一步分析车身的垂直、侧倾、俯仰运动特性.首先取h=0.0036m,结果如图7、图8和图9所示.
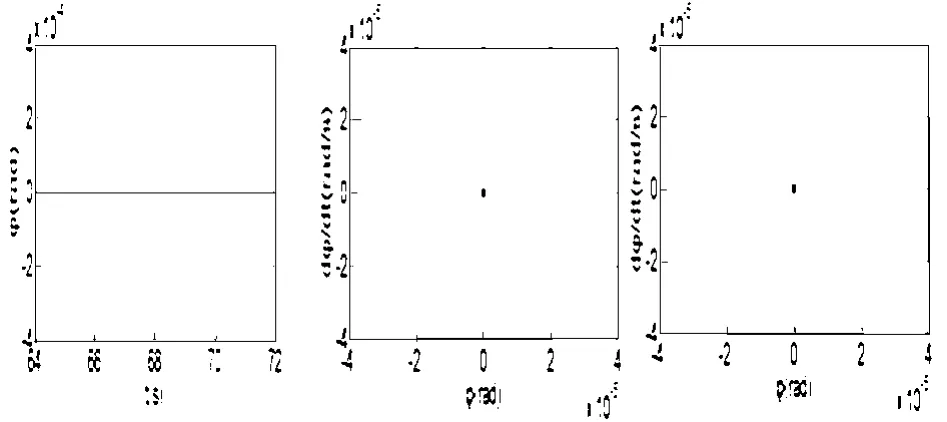
图8 减速带高度h=0.0036m,车身侧倾运动时间历程图、相位图、Poincaré截面Fig.8 Time history,phase portrait and Poincaré map of φ for h=0.0036m
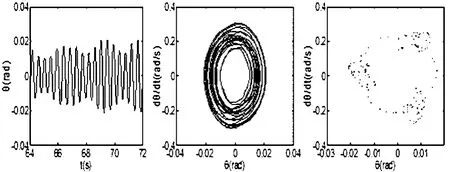
图9 减速带高度h=0.0036m,车身俯仰运动时间历程图、相位图、Poincaré截面Fig.9 Time history,phase portrait and Poincaré map of for h=0.0036m
从图8可以看出,车身的侧倾运动趋于稳定.分析图7和图9,车身垂直和俯仰运动的时间历程图无周期性,相位图由许多相环组成,Poincaré截面上的点分布混乱.结果表明,在h=0.0036m时,车身的垂直、俯仰运动形式为混沌运动.
其次取h=0.0041m,结果如图10、图11和图12所示.图10对应车身垂直运动的时间历程图,相位图和Poincaré截面.很显然,车身垂直运动的时间历程图无周期性,相位图由许多相环组成,Poincaré截面上的点分布混乱,表明在h=0.0041m时,车身的垂直运动为混沌运动.图11对应车身侧倾运动.很显然,车身的侧倾运动趋于稳定.从图12可以看出,车身俯仰运动的时间历程图无周期性,相位图由许多相环组成,Poincaré截面上的点组成三个圆环,表明车身的俯仰运动为三倍拟周期运动.
进一步分析可知,车身垂直方向发生混沌运动的区间为[0.0030,0.0044];车身俯仰运动发生混沌运动的区间为[0.0030,0.0038];车身侧倾运动在整个区间都趋于稳定;车身俯仰运动在区间[0.0038,0.0044]内为三倍拟周期运动.所以当汽车以车速v=12m/s通过高速公路上连续分布的减速带时,为避免发生混沌运动,减速带的高度应大于0.0044m.这为高速公路特殊路段上设计减速带提供了理论依据.

图10 减速带高度h=0.0041m,车身垂直运动时间历程图、相位图、Poincaré截面Fig.10 Time history,phase portrait and Poincaré map of z for h=0.0041m

图11 减速带高度h=0.0041m,车身侧倾运动时间历程图、相位图、Poincaré截面Fig.11 Time history,phase portrait and Poincaré map of for h=0.0041m

图12 减速带高度h=0.0041m,车身俯仰运动时间历程图、相位图、Poincaré截面Fig.12 Time history,phase portrait and Poincaré map of θ for h=0.0041m
混沌现象只有在非线性系统才会出现,是确定性系统中的不规则运动.下面具体分析在连续减速带激励下,汽车俯仰运动由周期运动通向混沌运动的途径.图13和图14给出了车身俯仰运动随减速带高度变化时的Poincaré截面演变过程.

图13 车身俯仰运动的Poincaré截面,(h=0.0045m,h=0.00442m,h=0.0044m)Fig.13 Poincaré map of θ for(h=0.0045m,h=0.00442m,h=0.0044m)

图14 车身俯仰运动的Poincaré截面,(h=0.00388m,h=0.00386m,h=0.0038m)Fig.14 Poincaré map of θ for(h=0.00388m,h=0.00386m,h=0.0038m)
分析图13、图14,可以看出车身俯仰运动通向混沌的道路可以分为两步.第一步:由周期运动到拟周期运动过程,在图13中,当h=0.0045m时,Poincaré截面上有三个点,表明此时的运动为周期三运动,当h减小到0.00442m时,Poincaré截面上的三个点向周围扩散,当h减小到0.0044m时,Poincaré截面上的点组成三个圆环,运动已经变为三倍拟周期运动;第二步:由拟周期运动到混沌运动,从图14中可以看出,h减小到0.00388m时,Poincaré截面上三个圆环分别向周围逐渐破裂,当h减小到0.00386m时,Poincaré截面上三个圆环已经明显破坏,此时的运动已经具有明显的混沌运动特性,当h减小到0.0038m时Poincaré截面上的点完全混乱分布,此时汽车俯仰运动已经变为混沌运动.
3 结论
本文数值研究了连续减速带激励下具有磁流变悬架系统七自由度汽车的非线性动力学行为.结果表明一定高度范围的减速带可激发汽车混沌运动.因此,汽车设计时应充分考虑连续减速带激励对其运动特性的影响,避免发生混沌振动等有害运动,实现平稳安全行驶.
1 郑剑.减速带激励下非线性汽车悬架系统动力学特性研究[硕士学位论文].重庆:重庆大学,2010:30~52(Zheng J.Study on dynamics character of nonlinear vehicle suspension system due to speed control humps impact[Ms Thesis].Chongqing:Chongqing University,2012:30 ~ 52(in Chinese))
2 Li S,Yang S,Gao W.Investigation on chaotic motion in hysteretic non-linear suspension system with multi-frequency excitations.Mechanics Research Communications,2004,31(2):229~236
3 李韶华,杨绍普.拟周期激励下滞后非线性汽车悬架的混沌.振动与冲击,2003,22(3):61~64(Li S H,Yang S P.Chaos in suspension system with hysteretic nonlinearity under quasi-period excitation.Journal of Vibration and Shock,2003,22(3):61 ~64(in Chinese))
4 马新娜,杨绍普.时滞在磁流变主动控制系统中的影响.动力学与控制学报,2012,10(3):228~234(Ma X N,Yang S P.Effect of time-delay on MRD active control system.Journal of Dynamics and Control,2012,10(3):228~234(in Chinese))
5 钱长照.车桥耦合振动的摄动分析方法.动力学与控制学报,2009,7(4):375~379(Qian C Z.Perturbation method for coupling vibration system.Journal of Dynamics and Control,2009,7(4):375 ~379(in Chinese))
6 Zhu S J,Zheng Y F,Fu Y M.Analysis of non-linear dynamics of a two-degree-of-freedom vibration system with non-linear damping and non-linear spring.Journal of Sound and Vibration,2004,271:15~24
7 Von W U.On non-linear stochastic dynamics of quarter car models.International Journal of Non-Linear Mechanics,2004(39):753~765
8 徐赵东,沈亚鹏.磁流变阻尼器的计算模型及仿真分析.建筑结构,2003,33(1):68~70(Xu Z D,Shen Y P.The calculation model and simulation of magnetorheological damper.Journal of Building Structures,2003,33(1):68 ~70(in Chinese))
9 方子帆.基于MR阻尼器的半主动悬架控制方法研究[博士学位论文].重庆:重庆大学,2006(Fang Z F.The study of the semi-active suspension’s control method based on the MR damper[PhD Thesis].Chongqing:Chongqing University,2006(in Chinese))
*The project supported by the National Natural Science Foundation of China(10972179,11272242)
† Corresponding author E-mail:wying36@163.com
NONLINEAR VIBRATION ANALYSIS FOR AUTOMOBILE STIMULATED BY SPEED CONTROL HUMP*
Wu Ying1†Li Jiajia1Nong Duomin2,3Liu Shaobao1
(1.State key Laboratory for strength and Vibration,School of Aerospace,Xi’an Jiaotong University,Xi’an710049,China)(2.Guangxi Liugong Machinery Co.,Ltd.,Liu Zhou545001,China)(3.Department of Engineering Mechanics,School of Civil Engineering and Architecture,Xi’an University of Technology,Xi’an710048,China)
This paper investigated the nonlinear dynamic behavior of seven degree-of-freedom automobile with suspension system of sigmoid magneto-rheological damper stimulated by speed control hump(SCH).Based on the Lagrange equations,the two-order differential equations were developed to describe the motion of automobile,and the fourth-order Runge-Kutta method was used for the numerical simulation.The bifurcation was analyzed by taking the height of SCH as bifurcation parameter,and the movements of the automobile at some values of height were analyzed by using time series,phase portrait,Poincaré map.The height ranges of SCH were obtained when the chaos vibration appeared,and the route to chaos was analyzed.
speed control hump, magneto-rheological damper, nonlinear, bifurcation, chaos
5 June 2013,
8 June 2013.
10.6052/1672-6553-2013-072
2013-06-05 收到第 1 稿,2013-06-08 收到修改稿.
*国家自然科学基金资助项目(10972179,11272242)
E-mail:wying36@163.com
