基于非线性混沌理论的非平稳信号的比较分析*

2014-09-17魏春雨杨威王梓卉敏韩清鹏

动力学与控制学报 2014年2期

关键词：振动误差预测

魏春雨杨威王梓卉敏韩清鹏

(辽宁科技大学机械工程与自动化学院，鞍山 114051)

基于非线性混沌理论的非平稳信号的比较分析*

魏春雨杨威王梓卉敏韩清鹏†

(辽宁科技大学机械工程与自动化学院，鞍山 114051)

本文研究采用基于非线性混沌理论的两种非线性参数估计方法(代替数据法和Lyapunov指数估计法)对非平稳信号进行分析．首先对上述两种非线性方法的具体算法进行介绍，然后对两组本质不同的非平稳振动信号进行对比分析．这两组信号是通过测试具有不同非线性约束边界条件的薄壁构件获得．分析结果表明，在时域波形上直观相似的非平稳信号，用上述非线性混沌分析的方法可以有效地加以定量区分．

非线性混沌理论，非平稳信号，代替数据法， Lyapunov指数

引言

人们通常考虑振动信号是否具有平稳或非平稳的性质，而线性或非线性特性则是对其源系统而言［1］．在工程中，大多数系统所测得的信号是非平稳的，而系统是非线性的．区分非平稳信号在现代信号处理中，非平稳信号的处理是最为活跃、发展最为迅速的方向之一［2］，在通讯、雷达、自动控制、模式识别、机械振动和生物医学工程等领域广泛应用．通过分析信号的时变特征，构造合适的时频分布并进行恰当的处理，达到不同的信号处理目的．近年来，人们采用多种时频分析方法对非线性和非平稳信号进行分析，包括小波分析、Wagner－Ville分布等［3－6］．此外，还有许多非线性分析的方法也加以应用［7－9］．但是，从非线性角度，基于混沌理论的一些方法，如Lyapunov指数和分数维，对于具有非线性特性的非平稳信号分析更为有效［10，11］．另外，对信号进行混沌辨识，并将非线性信号从随机噪声中区分出来往往是比较困难的．这是因为混沌信号和随机噪声信号通常都具有相似的宽频特征．目前区分混沌和噪声的常用方法主要有两类:维数估计方法和非线性预测法．第一类方法是基于随机只能存在无限维吸引子的原理，而有限维吸引子意味着混沌，如在 Grassberger－Procaccia算法中所指出的那样［10］．第二类方法则是根据时间序列的非线性预测原理、混沌具有不同于随机数据的短期预测性的性质来区分混沌和噪声信号．也就是对于一个混沌时间序列，它的预测值和实际值之间的相关系数会随预测时间的增加而减弱;而对于随机时间序列，这种相关性不会因预测时间的增加而变化．

本文针对由金属薄壁构件实测得到的具有不同非线性约束边界条件、不同性质的非平稳振动信号，采用两种不同的非线性预测方法进行对比分析，即代替数据法和Lyapunov指数方法．其中代替数据法主要参考了文献［12］．这种方法可以通过对比混沌信号和噪声信号(包括白噪声和有色噪声)的预测误差分布及其所对应的代替数据集的预测误差分布的差异来实现．Lyapunov指数是某过程在其相平面内相邻轨线的平均发散速率的量化定义．正的Lyapunov指数(一个或多个)是进行混沌辨识的重要指标．时间序列的Lyapunov指数的估算方法有多种，见文献［13－17］．

1 两种非线性预测方法的算法原理

1．1 基于代替数据法的混沌辨识

(1)信号的代替数据集的生成

信号所对应的代替数据集可以由基于时间序列的 Gauss随机过程假设得到．本文通过对非Gauss过程有效的非线性直方图变换方法来实现．对于一个原始信号，一般生成包含128个不同时间

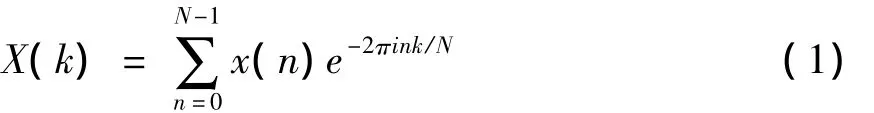
接下来，通过将上述复数乘以eiφ使其相位角在每个频率上随机化，其中φ是归一化的、在［0，2π］区间内变化的随机量，得到新的X'(k)．对其进行逆傅立叶变换，可以得到Gauss型代替数据序列，也就是得到具有原始信号相同的幅值分布形式的代替数据序列x'(n)，如下式序列的代替数据集．

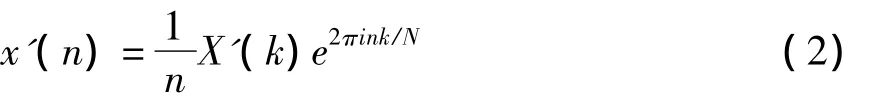
进行直方图变换时，首先生成一个与原给定时间序列长度相同的Gauss随机数集合，然后对这个Gauss数据集的顺序进行重排．新的时间序列应是具有Gauss概率密度函数分布的、与原序列相对应的非线性尺度变换的结果．对于原始信号是Gauss随机的情况，变换后的序列也具有Gauss分布．第一步是，将时间序列x(n)进行傅立叶变换，得到

由于上式的逆傅立叶变换是实数，其相位角具有对称性，即φ(k)=－φ(N－k)．

(2)统计量的计算

由于低维混沌意味着其系统在短期内可以视为是确定性的，而随机过程与此不同．可以将预测误差ε取为统计量．首先利用状态变量x将时间序列x(n)进行相空间重构，采用时间滞后的嵌入法，即

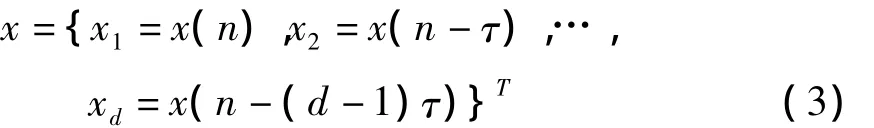
其中嵌入维数d应该满足d≥2D+1，D是系统的真实吸引子维数，在实际计算过程中往往需要依靠经验选取．注意到这里的n小于数据长度N，即1≤n≤N．时间滞后点τ的选择有时具有一定随意性，在这里简单地取作1．

下面将时间序列的数据点集分成长度相等(Nf=Nt)的拟合集和检验集两部分．在拟合集中，寻找与当前点欧几里德距离最为相邻的k个状态点．这k个当前时刻为m的状态点与对应的下一时刻m+1的状态点组成如下k个点对:

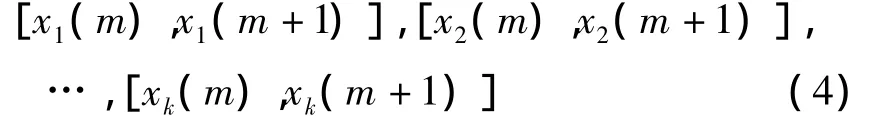
采用如(5)式所示的预测公式对这k个点对进行拟合

其中，a和b是拟合系数，¯x是x的预测点．

接下来，计算检验集Nt中的所有点对应的预测误差，将得到N/2个预测误差．预测误差的定义为由(6)式得到的下一时刻(m+1)的预测值和实际值的差值．

进行混沌识别的统计量取为上述全部预测误差的平均绝对误差(MAE)．

(3)假设检验

对于生成的所有代替数据集，根据如下公式(7)来计算显著度:

其中，QD是由原始信号时间序列计算得到的统计量值(MAE值)，us和σs分别是由生成的128个代替数据序列计算得到的统计量值的均值和方差．

计算得到的χ值可以用于分析原始信号数据和代替数据的差异．如果χ是一个较小的数，这意味着原始信号和它的所有代替数据集具有相同的性质，因此随机假设可以接受，也就是原始信号是随机的．相反，如果χ值较大，可以认为代替数据序列与原始信号有较大的差别，拒绝随机假设．

更进一步，为了辨识原始数据序列是随机的还是混沌的，定义如式(8)所示的置信判据．拒绝随机假设的最大概率也就是相应的显著度P定义为

其中erf()为数据序列所有元素的误差函数，其定义如式(9)所示．

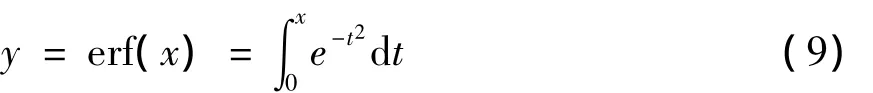
根据经验，如果计算得到的概率P值小于0．05，原始信号数据将显著地不同于它的代替数据集，这时可以拒绝随机假设，认为原始信号在95%置信度下是混沌的．如果P值大于0．05，则认为原始信号是随机的(95%置信度)．当然，这里的临界值0．05可以根据实际情况的不同而不同．

1．2 Lyapunov指数的估计算法

按数值大小进行重排，得到该时间序列的Lyapunov指数如下

因为p是一个较大的整数，由此得到的Lyapunov指数是每个相点在其轨线上以指数形式发散的统计平均值．在上述Lyapunov指数中，一个或多个Lyapunov指数可能都是正的．根据非线性理论，正的Lyapunov指数意味着该时间序列(信号)是混沌的．

2 实例

对某薄壁构件进行宽频随机激振试验．外激励为500Hz范围内的标准白噪声，对构件的振动响应进行测试．由于是两种性质不同的非线性边界条件，得到的构件振动响应呈现出明显的非平稳振动信号特征，其中应该蕴含着不同的特征．

图1所示为测试得到的两组振动响应时间信号，分别记为x1和x2．它们所对应的功率谱密度(PSD)如图2所示．从图(2)只能看出，这两个信号都具有0－500Hz有限频带分布的特征，形状上仅有稍微区别．因此，仅从图1和图2人们很难区分这两个信号．

首先从非线性定性分析的角度对这两组信号进行比较．可以利用连续峰值来绘制这两个信号的伪Poincare映射图．设是一个时间序列的峰值集合，则它的伪Poincare映射图是指对应绘出的点图．如果考虑采样误差，信号的周期点会在伪Poincare映射图表现为一个较小的区域．而伪Poincare映射图中出现分散的点区域时，根据非线性混沌理论，表明存在不规则或奇怪吸引子．对于这两个信号x1和x2，它们的伪Poincare映射图如图3所示．从图3(a)和(b)可以看出，信号x1和x2的伪Poincare映射图在形貌上还是有区别的．

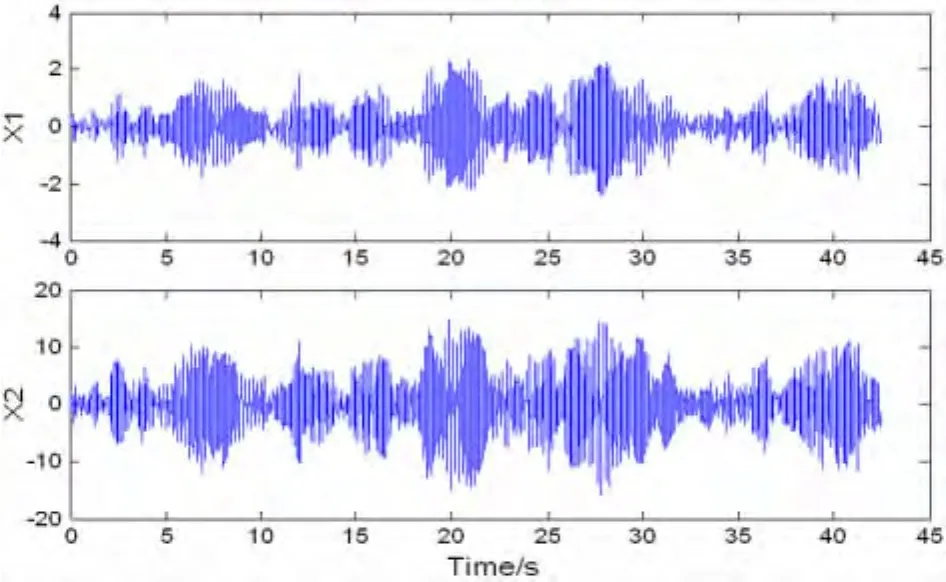
图1 非平稳时间序列信号x1和x2Fig．1 Non － stationary time series of x1and x2

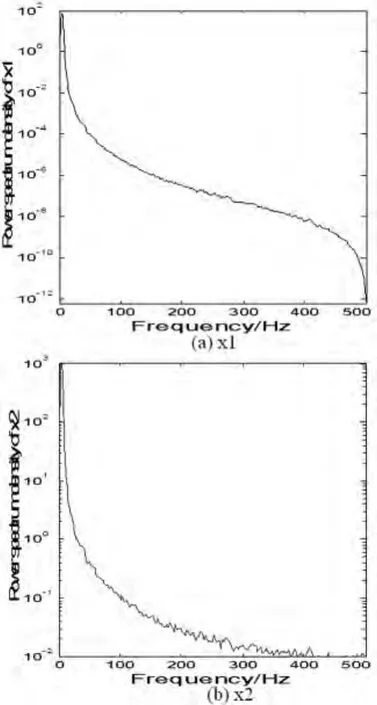
图2 x1和x2的功率谱密度Fig．2 Power spectral densities of x1and x2

根据前文所介绍的非线性混沌分析理论，用代替数据法计算得到的关于x1和x2的概率P值见表1．如1．1节所言，如果P值小于0．05，则拒绝随机假设，信号的混沌特性得到辨识(95%的置信度)．因此信号x1和x2都可以认为是混沌时间序列．另外，从表1中的其它特征值来看，如QD，us和χ，也可以对这两组信号加以定量地对比区分．

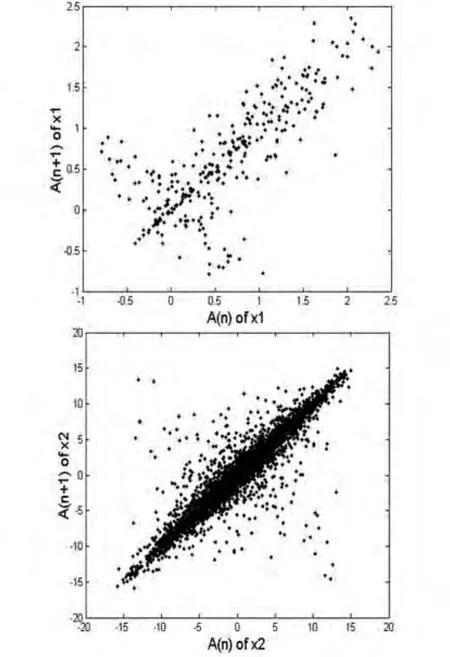
图3 x1和x2伪Poincare映射图Fig．3 Pseudo Poincare mapping portraits of x1and x2

计算得到的x1和x2的Lyapunov指数如表2所示．在估算这两组信号的Lyapunov指数的过程中，相空间重构的嵌入维数设为5，滞后点数设为7．从表2可以看出，x1信号有2个正的Lyapunov指数，即 1．1785、0．1846，信号x2有 3 个正的 Lyapunov指数，即 0．9674、0．1857 和 0．0184．所以，这两组信号可以视为是混沌的，但具有不同的混沌阶数．

表1 代替数据法得到的x1和x2的特征参数数值Table 1 Characteristic parameter values of x1and x2by surrogate data method

表2 估算得到的x1和x2的Lyapunov指数Table 2 Lyapunov index of estimated x1and x2

3 结论

本文利用基于混沌理论的非线性预测方法对非平稳信号进行了比较分析．从定量分析研究的角度，所采用的代替数据法和Lyapunov指数估计方法对区分具有不同非线性性质的非平稳信号是有效的．

对于两个典型的非平稳振动信号x1和x2，代替数据法所得到的特征参数的数值是互不相同的，估算得到的最大Lyapunov指数也是正的．根据代替数据法中的概率值的大小可以看出，x1比x2具有更明显的混沌特征，但是x1有2个正的Lyapunov指数，而x2有3个正的Lyapunov指数．

1 Kantz H，Schreiber T．Nonlinear time series analysis．Cambridge:Cambridge University Press，1999

2 张贤达，保铮．非平稳信号分析与处理．北京:国防工业出版社，1998(Zhang X D，Bao Z．Nonstationary signal analysis and processing．Beijing:National Defence Industry Press，1998(in Chinese))

3 He Zhengjia，Meng Qingfeng，Zhao Juyuan，et al．Timefrequency(scale)analysis and diagnosis for nonstationary dynamic signal of machinery．International Journal of Plant Engineering and Management，1996，1(1):40 ～47

4 Meltzer G S，Ivanov Y Y．Fault detection in gear drives with non－stationary rotational speed－ Part I:the time－frequency approach．Mechanical Systems and Signal Processing，2003，17(5):1033 ～1047

5 Wang Wenyi，Harrap M J．Condition monitoring of rolling element bearings by using cone kernel time－frequency distribution．In:Processings of the SPIE Conference on Measurement Technology and Intelligent Instrument．Bellingham，WA，1993:290～298

6 Katvonik V，Stankovic L．Instantaneous frequency estimation using the Wigner distribution with varying and datadriven widow length．IEEE Transactions on Signal Processing，1998，46(9):2351 ～2325

7 Casdagli M．Nonlinear prediction of chaotic time series．Physica D，1989，35(3):335～356

8 Engbert R．Testing for nonlinearity:the role of surrogate data．Chaos，Solitons＆Fractals，2002，13(1):79 ～84

9 Banbrook M，Ushaw G，McLaughlin S．Lyapunov exponents from a time series:a noise－robust extraction algorithm．Chaos，Solitons＆Fractals，1996，7(7):973 ～976

10 Theiler J，Eubank S，Longtin A，et al．Testing for nonlin－earity in time series:the method of surrogate data．Physica D:Nonlinear Phenomena，1992，58(1－4):77 ～94

11 Yonemoto K，Yanagawa T．Estimating the Lyapunov exponent from chaotic time series with dynamic noise．Statistical Methodology，2007，4(4):461 ～480

12 Kennel M，Isabelle S．Method to distinguish possible chaos from coloured noise and to determine embedding parameters．Physical Review A，1992，46(6):3111 ～3118

13 Kantz H．A robust method to estimate the maximal Lyapunov exponent of a time series．Physics Letters A，1994，185(1):77～87

14 Wolf A，Swift J V，Swinney H L，et al．Determining Lyapunov exponents from a time series．Physica D:Nonlinear Phenomena，1985，16(3):285 ～317

15 Rosenstein M T，Collins J J，Luca C J．A practical method for calculating largest Lyapunov exponents from small data sets．Physica D:Nonlinear Phenomena，1993，65(1－2):117～134

16 周良强，陈芳启，葛鹏．一类大展弦比机翼非线性模型的稳定性与分岔．动力学与控制学报，2012，10(3):222 ～227(Zhou L Q，Chen Q F，Ge P．Stability and bifurcation for a nonlinear model of high－aspect－ratio wings．Journal of Dynamics and Control，2012，10(3):222～27(in Chinese))

17 吕书锋，胡宇达．正交各向异性叠层板的非线性主共振分析．动力学与控制学报，2009，7(1):35～38(Lu S F，Hu Y D．Nonlinear principal resonance of orthotropic laminated plates．Journal of Dynamics and Control，2009，7(1):35～38(in Chinese))

*The project supported by the National Natural Science Foundation of China(10972192)

† Corresponding author E－mail:han1011@163．com

COMPARATIVE ANALYSES OF NON-STATIONARY SIGNALS BASED ON NONLINEAR CHAOTIC THEORIES*

Wei Chunyu Yan WeiWang Zihuimin Han Qingpeng†
(College of Mechanical Engineering，Liaoning Science and Technology University，Anshan114051，China)

In the paper，two nonlinear estimation methods based on nonlinear chaotic theory，surrogate data method and Lyapunov exponents，are used to distinguish the difference of non－stationary signals．After brief introduction of the corresponding algorithms，two typical different non－stationary signals measured from a thin－plate structure with different nonlinear constraining boundaries are taken to compare by using the above two methods respectively．The obtained results demonstrate that the apparently similar signals are distinguished effectively in quantitative way with applying above nonlinear chaotic analyses．

nonlinear chaotic theory， non－stationary signals， surrogate data method， Lyapunov exponents

9 October 2012，

1 July 2013．

10．6052/1672－6553－2014－014

2012－10－09 收到第 1 稿，2013－07－01 收到修改稿．

*国家自然科学基金资助项目(10972192)

E－mail:han1011@163．com