结构中频振动分析的混合方法

王坤 赵阳 张斌

(1．中国航天科工集团第九总体设计部，武汉 4 30040)(2．哈尔滨工业大学航天学院，哈尔滨 1 50001)

结构中频振动分析的混合方法

王坤1†赵阳2张斌1

(1．中国航天科工集团第九总体设计部，武汉 4 30040)(2．哈尔滨工业大学航天学院，哈尔滨 1 50001)

针对结构振动的中频问题，提出了一种新的混合分析方法．具有低模态密度的子结构利用有限元建模，高模态密度子结构利用波动方法建模，并利用边界处的位移连续和力平衡条件进行求解．以耦合梁结构为例，给出了具体的计算过程，通过解析方法进行了仿真验证．结果表明了此混合方法的有效性．进一步地计算了高频子结构的能量密度响应，并且通过对比说明，此方法在计算边界位置的能量密度响应时可以得到精确度更高的结果．

波动， 有限元法， 中频振动， 混合方法， 能量密度

引言

振动分析方法按频域可以分为低频、中频和高频．在低频区域，波长相对于结构尺寸较长，结构内含有的波数较少，在此频域内，比较实用的方法是有限元法．高频振动时，结构内包含大量振动模态，有限元法需要增加单元的数量，以捕捉结构的振动特性，控制插值误差和污染误差［1］，计算量因此而增大，以至于在高频区域变得不可行．在高频区域，通常进行振动响应的能量分析，其中最重要的方法是统计能量分析(SEA)．SEA把声振系统按相似模态分为子系统，系统的统计行为是预先确定的，其主要变量为子系统振动的平均能量，因此大大减小了计算成本．SEA的主要不足是要求高模态密度，这限制了它只能用于高频情况，并且其预示的结果也比较粗略，针对每个子系统只有一个平均的能量响应预示结果．目前一些技术试图对统计能量分析进行改进，能量有限元［2－4］将时间和空间平均后的能量密度作为变量，也大大的减小了计算量，并且结合有限元技术，可以给出更为精细的响应预示．但其实用性还有待实践的进一步验证．

在低频和高频区域之外，还存在着中频区域，针对此区域有不少学者开展过研究［5，6］，目前中频区域还没有确定的定义，通常认为，在中频区域的结构振动存在着混合行为，部分子结构振动模态密集，重叠率高，称之为高频子结构，而另一部分子结构包含振动波数较少，适合用数值方法进行分析，称为低频子结构．基于此理念，最近几年中频问题的研究一般采用混合方法．Vlahopoulos等人发展了混合有限元方法，将有限元分析和能量有限元法结合起来以研究结构的中频响应［7，8］，Langley等人把有限元法和统计能量分析结合起来，低频区域用有限元分析，高频区域则利用统计能量分析［9，10］．此方法得到了成功的应用，目前流行的声振分析软件VA One就是利用此技术．

波动方法的研究为振动响应预示提供了另一种思路．波动方法视振动以波的形式在结构中传播，能够较好地捕捉结构局部的振动特性，并且其计算效率高，适合于高频领域的计算．一直以来都有学者致力于用波动方法解决振动响应的预示与控制［11－13］．本研究利用波动方法与有限元法结合，采用确定的边界条件，对高频振动的子结构进行行波方法求解，而对于低频子结构部分进行有限元求解，为中频结构的响应预示提供了另一种可能的解决方法．波动方法的另一特点是对振动能量的传播给出了一种更为直观的解释，Lyon等人首先用波动方法计算了统计能量分析的耦合损耗因子［14］．目前用于高频计算的能量有限元方法［2－4］，其基础就是结构振动的波动解，波动法在一定程度上与能量有限元法是统一的．而且能量有限元法忽略了近场解，在边界处会引起较大误差，而波动方法考虑了边界效应，在边界附近可以得到比能量有限元法更为精确的响应．利用波动方法结合有限元研究结构的高频振动响应，可以为结构的中高频振动响应的预示提供新的思路．

1 混合方法建模

对于低频振动的子系统部分，可以采用有限元单元法建模

式中q为低频子结构的振动自由度，根据需要可以有不同的选择，通常情况下，选择结构某些离散位置上的位移和转角;F为结构所受外力的向量;S为结构的总刚度阵，可以表示为－ω2M+iωC+K，其中M为结构的质量阵，C为阻尼阵，K为刚度阵．此表示形式根据自由度的特点可以分为三部分:与高频子结构的连接自由度，子结构的边界自由度和剩余自由度．

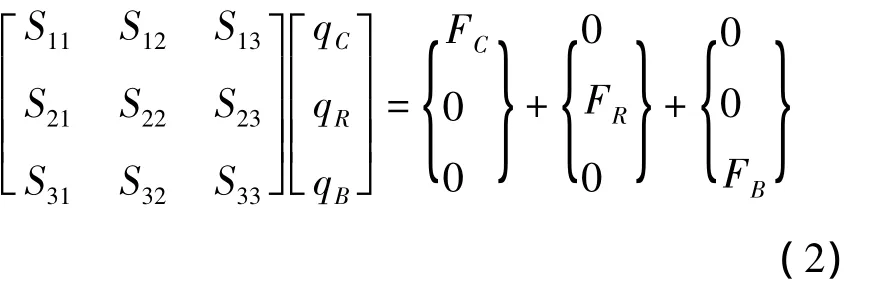
对于高频振动的子结构部分，可以利用波动的思想表示为

W为与位置有关的位移函数项，eiωt表示位移随时间的变化．

在高频子结构与低频子结构的连接处，存在着位移连续和力平衡条件

式中u(W)和θ(W)为波动解的位移和转角，Q(W)和M(W)为相应的剪力和弯曲．考虑到高频子结构的边界只影响边界附近较小范围内的振动特性，在精度要求不高时，边界条件产生的近场解通常可以忽略，在此情况下，式(3)只表示了远离结构边界的远场变量，联合上(2)－(5)式，可以求得结构的全局响应．如果需要考虑边界附近的响应影响，式(3)中加入近场项，并结合高频结构的边界条件，可以求得边界处的响应．

2 实例计算

针对耦合梁的情况，研究此混合计算方法的有效性．如图1所示，振动结构由两部分组成，左边为梁1，设为高频子结构，利用波动法求解，右边为梁2，与梁1直接连接，其右端边界为固支，为低频子结构，利用有限元法建模．由(2)式，取梁振动的位移和转角为变量，则

梁2的振动形式表示如下

由上式求得连接处的自由度形式为

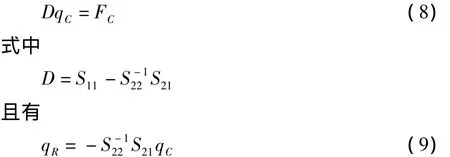
式(8)表示为矩阵形式

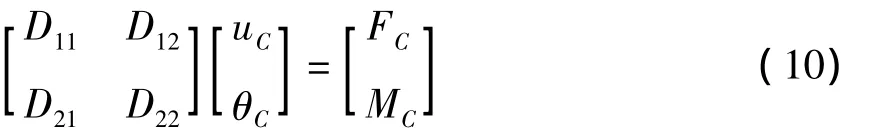
式中uC为连接处位移，θC为连接处转角，FC和MC为对应的剪力和弯矩．

图1 耦合梁结构Fig．1 A coupled － beam system

对高频子结构梁1，远场解的位移表达式为

A1和B1为波动系数，k1为梁的波数．此情况下相当于梁中波幅值为A1的右行波，遇到边界后部分透射，部分反射回来，反射部分幅值为B1．计算得到的时间和空间平均的能量密度响应为

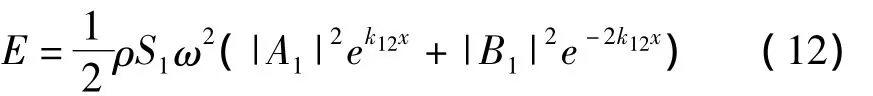
式中，k12为梁1波数的虚部．此情况只考虑了远场解，与能量有限元法得到的结果相同．产生幅值为A1的行波的激励F可与A1的关系可以通过无限梁的导纳来近似求得

式中Y∞为无限梁的导纳［15］

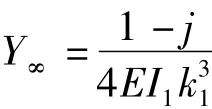
在梁的连接位置，为提高求解精度，加入近场解的影响

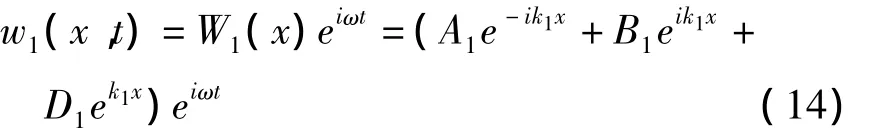
D1为近场衰减波的系数．

加入近场解的能量密度由下式计算

式中k11为梁1波数的实部．在连接处位移转角连续，力和力矩平衡，则有

式中EI1为梁1的弯曲刚度．

取连接处为坐标原点，得到方程组的矩阵形式如下所示

解以上方程组可以求得边界自由度qC与波动系数B1和D1．qC代入式(9)可以得到剩余自由度qR．

3 振动的解析解

结构振动的解析解通过波动方法求解，对高频子结构，只考虑了连接处近场解影响．而低频子结构由于近场解影响范围较大，必须加入其影响．则梁1和梁2的表达式如下

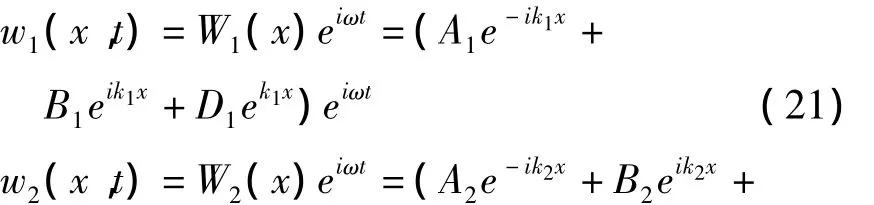
其中波数为

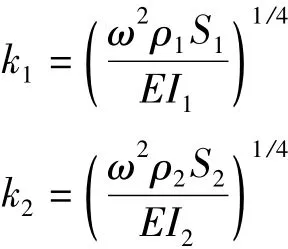
由连接处位移和转角连续及力和力矩平衡条件

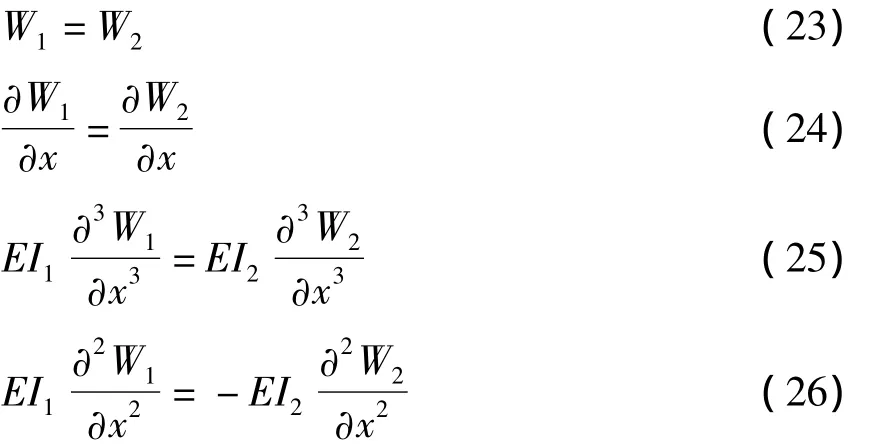
梁2固支边界处位移和转角为零

解方程(21)－(28)式可以求得结构振动的解析的响应表达式．

4 仿真结果分析

单位幅值激励作用下，对结构进行了仿真分析，两支梁长L1=L2=2m，阻尼比 η1=η2=0．01，梁1和梁2的线密度分别为ρS1=200kg/m和ρS2=100kg/m，梁1的弯曲刚度EI1=7200(1+iη)Nm2，梁 2 的弯曲刚度EI2=3000(1+iη)Nm2，得到了圆频率为0～500rad/s范围内的响应结果．

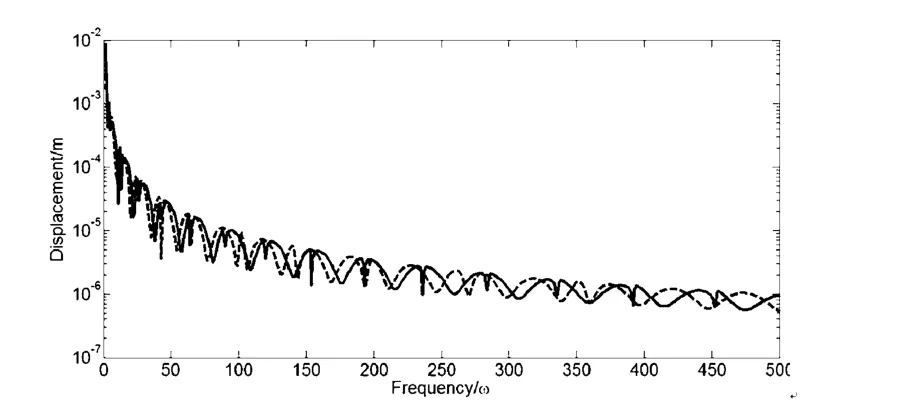
图2 6单元时梁1的位移对比Fig．2 Displacement of beam 1 using 6 elements

图2和图3给出了梁1中点位置的位移响应，图2中实线为解析解的响应结果，虚线为混合解法的响应结果，其中梁2划分为6个单元．图3中实线为解析解的响应，虚线为混合解法的响应，梁2划分为60个单元．由图2可以看到混合法在整体上与解析解吻合，图3显示，经过单元加密后，混合解法的预示精度有了很大提高，已经能够很好的捕捉共振峰值．对梁2的中点位移，图4给出了60单元的混合解法与解析解的比较．可以发现混合解与解析解符合很好，对共振峰值的捕捉也很好．

图3 60单元时梁1的位移对比Fig．3 Displacement of beam 1 using 60 elements

图4 梁2的位移对比Fig．4 Displacement of beam 2

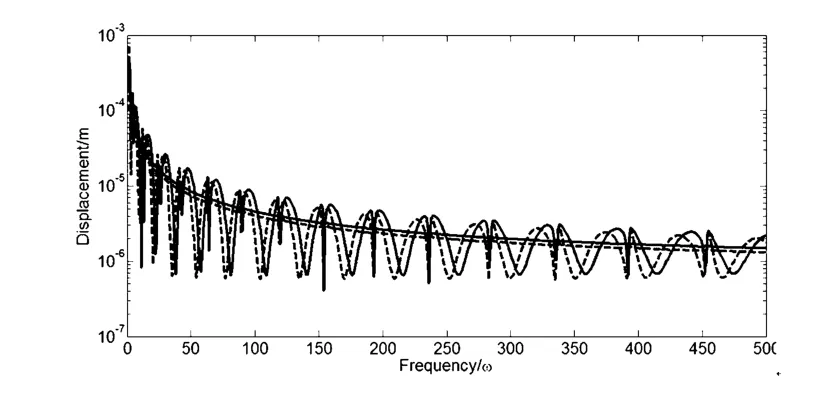
图5 梁1的能量密度Fig．5 Energy density of beam 1

图6 近场解对能量密度响应的影响Fig．6 Effects of near－ field on energy density

在进行高频响应分析时，能量有限元法是一种比较常用的方法，能量有限元的变量为时间和空间平均的能量密度，而通过波动解可以直接求得能量密度．图5给出了梁1振动的能量密度，图中实线为解析解计算的响应结果，虚线为混合解法的得到的响，波动的曲线是未进行平均的能量密度，平滑曲线为平均化后的能量密度．图中显示混合解法与解析解法在能量密度的求解上吻合很好，并且由图可以看出，平均化的能量密度在频域上得到的也是平均值．由于进行平均，计算量得到了大大减小，并且对于频率的变化不敏感．

为考虑近场解的影响，对梁1中点和与梁2连接处的能量密度响应进行了求解比较．图6中，a)图为远离边界的梁1中点处的能量密度响应比较，实线为未考虑近场解的响应曲线，星号为加入近场解的响应结果．可以看到两种情况下，响应结果是重合的，这表明在远离边界的位置，近场解的影响可以忽略．b)图中为连接处的能量密度响应比较，实线为未考虑近场解的响应曲线，虚线表示了加入近场响应后的结果，可以看到虚线值要明显比实线值高，这表明在连接处，近场解对响应的预示有较大影响，忽略近场解的得到的结果偏低．

5 结论

提出了利用波动法和有限元法混合的技术求解中频振动的响应问题，以耦合梁结构为对象进行了实例分析，仿真计算表明，混合方法能够有效地计算结构的振动响应，并且随着低频子结构有限单元密度的增加，会不断地逼近解析解．由于研究结构高频响应的能量有限元法的基础是波动解，此混合方法可以基于此思想直接求解高频子结构的能量密度响应，利用平均化的能量密度为变量可以大大减小计算量，本研究采用的混合方法的基础是有限元法和波动理论．后续工作需要集中在波动理论的研究上，才能进一步拓宽此混合技术的应用范围．

1 Zienkiewicz O C．The finite element method．New York:McGraw－Hill，1977

2 Nefske D J，Sung S H．Power flow finite element analysis of dynamic system:Basic theory and application to beams．Transactions of the ASME，1989，111(1):94～100

3 Bouthier O M，Bernhard R J．Simple models of the energetics of transversely vibrating plates．Journal of Sound and Vibration，1995，182(1):149 ～164

4 Cho P E．Energy flow analysis of coupled structures．West Lafayette:Purdue University，1992

5 Soize C．Reduced models for structures in the medium－frequency range coupled with internal acoustic cavities．Journal of the Acoustical Society of America，1999，106(6):3362～3374

6 Demet W，Hal B，Sas P，Vandepitte D．A computationally efficient prediction technique for the steady－state dynamic analysis of coupled vibro－acoustic systems．Advances in Engineering Software，2002，33:527～540

7 Vlahopoulos N，Zhao X．Basic development of hybrid finite element method for midfrequency structural vibrations．AIAA Journal，1999，11(37):1495 ～1505

8 Zhao X，Vlahopoulos N．A basic hybrid finite element formulation for mid－frequency analysis of beams connected at an arbitrary angle．Journal of Sound and Vibration，2004，296:135～164

9 Shorter P J，Langley R S．Vibro－acoustic analysis of complex systems．Journal of Sound and Vibration，2005，288:669～699

10 Shorter P，Langley R．On the reciprocity relation－ship between direct field radiation and diffuse reverberant loading．Journal of the Scoustical Society of America，2005，117(1):85～95

11 Audrain P，Masson P，Berry A．Investigation of active structural intensity control in finite beams:Theory and experiment．The Journal of the Acoustical Society of America，2000，108(2):612 ～623

12 Liu C C，Li F M，Huang W H．Active vibration control of finite L－shaped beam with traveling wave approach．Acta Mechanica Solida Sinica，2010，23(5):377 ～385

13 田浩，王有懿，刘春川．卫星框式结构扰动动态特性分析的行波方法．哈尔滨工业大学学报，2010，42(5):696～699(Tian H，Wang Y Y，Liu C C．Dynamics characteristic analysis of disturbance on satellite frame structure via travelling wave method．Journal of Harbin Institute of Technology，2010，42(5):696 ～699(in Chinese))

14 Lyon R，Eichler E．Random vibration of connected structures．Journal of the Acoustical Society of America，1964，36 7):344～1354

15 Cremer L，Heckl M，Petersson B A T．Structure－Borne Sound．Berlin:Springer，2005

† Corresponding author E－mail:alacarte@163．com

A HYBRID METHOD FOR THE ANALYSIS OF STRUCTURAL VIBRATION IN MEDIUM FREQUENCY

Wang Kun1†Zhao Yang2Zhang Bin1
(1．The9th Designing of China Aerospace Science＆Industry Corp．，Wuhan430040，China)(2．School of Astronautics，Harbin Institute of Technology，Harbin150001，China)

A new hybrid method was presented to predict vibration responses of structures in medium frequency．Finite element method was used to model subsystems with low modal density while wave method was for subsystems with high modal density．A coupled－beam system was exemplified to demonstrate the details．Compared with the analytical method，simulation results validate the hybrid method．Energy density response was obtained for the subsystem with high modal density．It is found that the hybrid method produces a more precise prediction in the vicinity of boundaries．

wave method， finite element method， medium frequency vibration， hybrid method， energy density

18 June 2014，

25 July 2014．

10．6052/1672－6553－2014－057

2014－06－18 收到第 1 稿，2014－07－25 收到修改稿．

E－mail:alacarte@163．com