基于变密度法的飞行器升力面结构多目标拓扑优化设计*

苗晓婷 许泉 刘 广 张 凤岗

(上海机电工程研究所，上海 2 01109)

基于变密度法的飞行器升力面结构多目标拓扑优化设计*

苗晓婷†许泉 刘 广 张 凤岗

(上海机电工程研究所，上海 2 01109)

为研究权衡结构刚度与低阶振动频率的飞行器升力面最优结构设计，提出两种多目标拓扑优化方案(约束法、结合约束法与评价函数法)．基于变密度方法，在约束法方案中将多目标优化转化为设定参考点位移约束和低阶振动频率约束下，求解结构质量最小化的优化问题．在结合约束法与评价函数法方案中，定义组合柔度指数为评价函数(结构柔度与振动频率的函数)，将多目标优化转化为设定低阶振动频率约束和体积分数约束下，求解结构最小组合柔度指数的优化问题．结果表明两种方案的优化结果具有一定的相似性，各有所长．优化设计不仅减轻了升力面结构重量，而且提高了结构的一、二阶振动频率．

多目标， 拓扑优化， 约束法， 评价函数法

引言

航天航空飞行器升力面的结构设计主要考核的参数为振动频率、刚度和质量，振动频率又是刚度和质量的函数，因此三个主要参数必须结合在一起考量，以求设计出最佳的升力面结构．连续体结构的多目标拓扑优化方法给升力面结构的优化设计开拓了新的思路．在计算机科学大力发展的辅助下，连续体结构的拓扑优化自本世纪以来得到了迅速的发展并广泛应用于航天航空、汽车、机械、医学及土木工程等领域．连续体结构拓扑优化设计主要包括均匀化方法［1］、变密度法［2－3］、ICM(independent，continous，mapping)方法［4－5］以及渐进结构优化方法(ESO)［6－7］，它们与有限元数值方法的结合推动了其在工程领域的实现［8］．其中变密度方法以连续变量的密度函数形式显式地表达单元相对密度与材料弹性模量之间的对应关系，寻求结构最佳的传力路线，以实现优化设计区域内的材料分布，具有程序易实现、计算效率快、计算精度高的优势．

拓扑优化过程是指在选定的设计区域内，满足给定的静力学、动力学约束条件下(包括位移、应力、频率、应变能、柔度和屈曲等)，寻求所设定的优化目标函数的最优解，从而确定最优的材料分布形式与结构设计方案．一个设计方案的好坏如果仅涉及一项设计指标，称为单目标优化设计问题;涉及多项设计指标，称为多目标优化设计［9］．在产品的初始设计阶段便充分考虑结构多目标拓扑优化设计技术的应用使最优化产品性能成为可能，大大缩短产品有效的设计周期，最大化工程利益．

多目标优化的难点在于如何在解决棋盘效应、网格依赖性和局部最优值等诸多数值困难的基础上，综合考虑不同的约束条件，协调多个优化目标之间的权重，求解多目标优化的最佳方案．尤其是针对动力学的多目标拓扑优化问题，必须同时考虑多个动力学约束条件使问题变得更加复杂．因此，目前连续体结构的多目标动力学拓扑优化技术被国内外学术界、工程界公认为最具有挑战性的课题和最具有生命力的研究方向．国内外学者针对多目标拓扑优化技术的优化算法、寻优策略的理论研究作了一定的工作［9－10］，然而其工程实践性并不理想;或针对单目标实现结构的动力学拓扑优化设计［11－13］，但在多目标的动力学拓扑优化方向的理论研究与工程实践甚少．

升力面结构作为飞行器的关键承力部件之一，结构刚度与低阶振动频率是避免发生静气弹效应，保证其对飞行器的高效操纵性的关键设计参数．本文基于变密度法中的SIMP法(solid isotropic material with penalization)使飞行器的升力面结构在满足轻量化的设计要求下，获得权衡刚度与一、二阶振动频率的最优设计方案．分别采用多目标拓扑优化设计的两种优化算法(约束法、结合约束法与评价函数法)，并对比优化结果，分析两种算法的有效性．

1 优化流程

1．1 数学模型

优化设计有三要素，即设计变量，优化目标函数和约束条件，设计变量是允许发生改变从而提高优化目标函数性能的一组参数;约束条件是对结构响应的限制条件，即随设计变量的改变对所引起的结构性能的限制;优化目标函数是设计变量的函数，优化过程即为在约束条件的限制下，寻求目标函数的最优解．其数学模型可表述为:

图1 优化求解流程Fig．1 The flow of optimization

式中，x1，x2，…，xi，xm是设计变量，如产品的结构尺寸，材料分布等;ft(x)是目标函数，可以为各种力学性能如振动频率、结构柔度、结构重量等;gj(x)是需要进行约束的设计响应，如结构的变形位移和应力水平．

1．2 求解流程

目前工程上高效、稳健的优化方法是采用数学规划方法，通过求解灵敏度构造近似显式模型，采用小步长迭代找到最优解，求解流程如图1所示．当连续两次迭代的目标值相差小于给定收敛容差时，优化问题求解收敛．

2 多目标优化方案

目前国内外普遍采取将多目标问题转化为单目标问题的方案以实现结构多目标优化，显然合理的转化方案决定着结构多目标优化的成败．同一研究对象，针对多个设计目标，可采用不同的数学转化模型，不同的转化模型对应不同的结果．对于实际的工程问题往往需要同时考虑多种转化方案，并对比不同的优化结果，最终根据工程实际需求采取最优方案．常用的转化方案可归纳为以下几种:

2．1 约束法

对比多个目标函数ft(x)，t=1，…，k的主次性，首先选取几个较为关键的目标(次要目标)分别进行优化，得到优化值，最后参照优化值以这几个次要目标作为约束条件并结合设计约束条件，求出最主要目标fi(x)的最优值．数学模型如下:

2．2 分层序列法

按照重要程度对多目标函数ft(x)，t=1，…，k进行排序，首先求出第1个目标的最优值，在此基础上求出第2个目标的最优值，依次类推，直到求出最后一个目标fk(x)的最优解．此方法的局限性在于目标函数重要程度的排列顺序对优化结果的影响较大，决定其工程实践性对设计师的经验要求较高．数学模型如下:

第1步

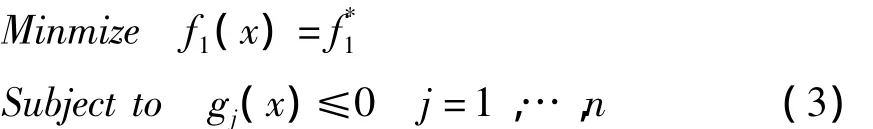
第2步

2．3 评价函数法

把多个目标函数ft(x)，t=1，…，k构造成一个目标函数－评价函数，然后对评价函数进行最优化．实际的工程问题中，可能多个目标函数的量纲是不同的，所以需要把每个目标函数事先规范化．主要包括以下几种方法:

(1)平方和加权法

先求出k个单目标优化问题的最优解，令评价函数

其中αt为事先给定的多目标的权重系数，最后再求minh(F)．

(2)规范目标法

与平方和加权法类似，先求出k个单目标优化问题的最优解，令评价函数

最后再求minh(F)．

(3)线性加权法

当目标函数的值均为正数或负数时，此方法在保证精度的基础上，相比前两种方法简化了计算求解过程．令评价函数为多个优化目标的线性加权

其中αt为事先给定的多目标的权重系数，最后再求minh(F)．

3 升力面结构优化与结果分析

3．1 有限元模型

本文以飞行器升力面结构为研究对象，实现综合考虑结构一、二阶振动频率与刚度的多目标拓扑优化设计．借助有限元分析软件HyperWork10．0中的Optistruct模块进行拓扑优化设计．Optistruct模块中的变密度法(SIMP方法)假设材料密度可在0～1之间连续变化，通过改变设计空间内材料的分布形式来搜索最优解，最后建议保留材料密度大的区域而删除材料密度小的区域．设定惩罚因子约束抑制介于0～1之间的单元，采用下限约束方法(minimum member size control)控制数值不稳定现象，通过约束拔模方向保证优化后结构的易加工性．定义收敛容差为0．5%，即当连续两次迭代的目标值相差小于0．5%时，求解收敛，优化结束．

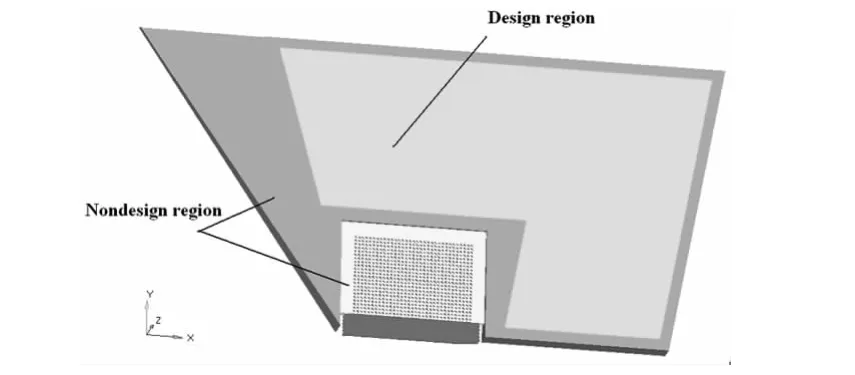
图2 升力面结构的有限元模型Fig．2 Finite element model of lifting－surface structure

升力面结构的有限元模型如图2所示，结构材料选用钛合金，ρ=4．5e －6kg/mm3，E=1．1e5MPa，υ=0．22．图中绿色区域为设计区域，黄色和紫色区域为非设计区域，在紫色非设计区域加载垂直于升力面上表面的压力载荷P=0．15MPa，在黄色区域内选取部分单元节点固支(以红色显示)．结构采用六面体和五面体一阶单元划分，单元大小均小于2．5，单元总数为 81750．

3．2 优化方案

首先计算优化前实心升力面的静态变形和一、二阶振动频率，变形如图3所示，最大变形量为3．439，选取1，2，3，4 点作为考察点，位移量分别列入表1中．结构一阶频率为 255Hz，二阶频率为307Hz，见表 2．

图3 优化前升力面的静态变形Fig．3 Static distortion of lifting－surface without optimization design

表1 考察点位移值Table 1 Displacement of the observed points

表2 结构的振动频率与组合柔度指数Table 2 Vibration frequency and combined compliance index(CCI)of the structure

升力面结构的振动频率是刚度和质量的函数，其刚度与一、二阶振动频率又是避免发生静气弹效应的关键设计参数．考虑升力面结构刚度与一、二阶振动频率的多目标优化问题实质是权衡如何提高结构刚度与一、二阶振动频率，并保证一、二阶振动频率的差异．以此为理论出发点，本文主要采用以下两种方案:

(1)方案1—约束法

首先分别对一、二阶振动频率进行单目标优化求出它们的最大值，如表2所示．由于参考点(1、2、3、4)位移大致决定升力面的结构变形，因此基于实心结构的位移值设定位移最大值的约束条件(表1)，并结合实心结构的频率值为下限，频率最大值为上限设定频率约束条件，求解结构质量最小化的优化问题．计算迭代54步后收敛，优化前结构质量为1．31kg，优化后结构质量为 0．92kg，可设计区域的质量减少了53%．优化后结构一、二阶振动频率分别有一定程度的提高(表2)，参考点位移略有增加(表1)．优化后升力面的静态变形如图4(a)所示，设计区域内材料分布情况如图4(b)所示．

(2)方案2—结合约束法与评价函数法

基于评价函数法中的线性加权法，如公式8所示，定义组合柔度指数(Combined Compliance index，CCI)为评价函数，在拓扑优化过程中综合考虑多个频率和静态子工况(载荷步、载荷工况)的组合．该指数定义为

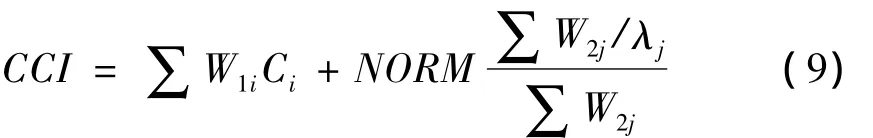
式中，Ci是结构的柔度，W1i是各工况柔度的加权值，λj是频率特征值，W2j是各特征值的加权值．它是一个定义在整个结构上的全局响应．标准化系数(NORM)用来对柔度和特征值对指数的贡献进行标准化．因为典型的结构柔度的数量级在1e4～1e6，而典型的特征值倒数的数量级在1e－5左右，如果不使用标准化系数，则线性静态柔度将决定优化结果．NORM的数值通常可用以下公式计算:

式中，Cmax是第一个迭代步中所有子工况(载荷步、载荷工况)中最大的柔度值;λmin是第一个迭代步中计算得到的最小的特征值．

图4 方案1优化结果Fig．4 Optimization design results of scheme 1

给定设计区域的体积分数约束为0．3～0．8，结合实心结构的频率值为下限，频率最大值为上限设定频率约束条件，求解结构组合柔度指数最小化的优化问题．计算迭代33步后收敛，优化后结构质量为0．94kg，可设计区域的质量减少了50%．优化后结构一阶振动频率的提高比方案1明显(表2)．结构最小组合柔度指数由优化前的2．65e3下降到2．44e3(表2)．优化后升力面的静态变形如图5(a)所示，参考点4的位移较方案1略有增加(表1)．设计区域内材料分布情况如图5(b)所示，图中白色圆圈所标记的区域材料分布较为分散．

图5 方案2优化结果Fig．5 Optimization design results of scheme 2

4 结论

对比两种方案，优化结果所展示的材料分布情况具有一定的相似性，如近似水平方向的材料分布情况，以及从舵叉部位向结构上边缘方向的材料分布情况．方案一优化后结构的材料分布情况比较集中，方案二优化后结构的一阶振动频率提高明显．相比方案一中的参考点位移约束，方案二的约束条件(振动频率、体积分数)与目标函数(组合柔度指数)均为整个结构的全局响应，易造成局部分散的材料分布情况，如图5中白色圆圈所标记的区域，这也是引起考察点4位移偏大的原因．两种方案的优化结果对结构设计均具有一定的指导意义，结合两种优化结果，设计升力面的蒙皮骨架结构形式，相比于升力面实心结构，不仅有效地减轻了重量，而且提高了一、二阶振动频率．本文采用合理的数学转化方案实现了飞行器升力面结构的动力学多目标拓扑优化设计，很大程度上缩短了研制周期，降低了生产成本，提高了产品性能．

1 牛小铁，董立立．机械结构拓扑优化设计研究现状及其发展趋势．煤矿机械，2012，33(9):5～7(Niu X T，Dong L L．Status of mechanical structural topology optimization design and development．Coal Mine Machinery，2012，33(9):5 ～7(in Chiniese))

2 Bendsoe M P，Sigmund O．Material interpolations in topology optimization．Archive of Applied Mechanics，1999，69:635～654

3 Mlejnek H P，Schirrmascher R．An engineer’s approach to optimal material distribution and shape finding．Computer Methods in Applied Mechanics and Engineering，1993，106(1－2):1 ～26

4 隋允康，彭细荣．结构拓扑优化ICM方法的改善．力学学报，2005，37(2):190～198(Sui Y K，Peng X R．The improvement for the ICM method of structural topology optimization．Chinese Journal of Theoretical and Applied Mechanics，2005，37(2):190 ～198(in Chiniese))

5 荣见华，葛森，邓果等．基于位移和应力灵敏度的结构拓扑优化设计．力学学报，2009，41(4):518～529(Rong J H，Ge S，Deng G，et al．Structural topological optimization based on displacement and stress sensitivity analyses．Chinese Journal of Theoretical and Applied Mechanics，2009，41(4):518 ～529(in Chiniese))

6 Xie Y M，Steven G P．A simple evolutionary procedure for structural optimization．Computers and Structures，1993，49(5):885～896

7 张爱林，杨海军，姚力．基于应变能的预应力平面实体结构拓扑优化设计．工程力学，2008，25(10):110～116(Zhang A L，Yang H J，Yao L．Topology optimization design of prestressed plane entity structures based on strain energy．Engineering Mechanics，2008，25(10):110 ～ 1 16(in Chiniese))

8 袁振，吴长春．采用非协调元的连续体拓扑优化设计．力学学报，2003，35(2):176 ～180(Yuan Z，Wu C C．Topology optimization of continuum structures using incompatible finite elements．Chinese Journal of Theoretical and Applied Mechanics，2003，35(2):176 ～180(in Chiniese))

9 孙晓辉，丁晓红．结构多目标拓扑优化设计．机械设计与研究，2012，28(4):1～9(Sun X H，Ding X H．Research on multi－objective topology optimization design methods for structure．Machine Design＆Research，2012，28(4):1～9(in Chiniese))

10 黄保科，孙军，王虎等．发动机曲轴轴承的多目标综合优化．汽车工程，2012，34(9):842 ～846(Huang B K，Sun J，Wang H，et al．Multi－objective integrated optimization of engine crankshaft bearings．Automotive Engineering，2012，34(9):842 ～846(in Chiniese))

11 张桥，张卫红，朱继宏．动力响应约束下的结构拓扑优化设计．机械工程学报，2010，46(15):45～51(Zhang Q，Zhang W H，Zhu J H．Topology optimization of structures under dynamic response constraints．Journal of Mechanical Engineering，2010，46(15):45 ～ 51(in Chiniese))

12 Zhu J H，Zhang W H，Qiu K P．Bi－directional evolutionary topology optimization using element replaceable method．Computational Mechanics，2007，40(1):97 ～109

13 Belblidia F，Bulman S．Constrained adaptive topology optimization for vibrating shell structures．Struct Multidisc Optim，2001，22(1):167～176

*The project supported by Sponsored by Shanghai Rising－Star Program(14QB1402400)

† Corresponding author E－mail:miaoxiaoting1983@126．com

MULTI-OBJECTIVE TOPOLOGY OPTIMIZATION DESIGN METHOD BASED ON PENALIZED DENSITY THEORY FOR AIRCRAFT LIFTING-SURFACE*

Miao Xiaoting†Xu Quan Liu Guang Zhang Fenggang
(Shanghai Electro-Mechanical Engineering Institute，Shanghai201109，China)

Taking account of the structural stiffness and the low order vibration frequencies，two schemes of multi－objective topology optimization were proposed to obtain the best aircraft lifting－surface structural design．Based on penalized density theory，the scheme one(named as constrain method)is to convert the multi－objective optimization to single－objective optimization by considering the minimum structural mass as the objective with constraints of reference points displacements and the low order vibration frequencies．The scheme two(named as the combination of constrain method and criterion function method)settles the multi－objective optimization by defining combined compliance index(CCI)as the objective，with the constraints of volume fraction and the low order vibration frequencies．The CCI is the function of structural compliance and low order vibration frequencies．Numerical results demonstrate the proposed schemes not only realize reducing the structural mass but also raise the first and second order frequencies．

multi－objective， topology optimization， constrain method， criterion function method

16 May 2014，

21 June 2014．

10．6052/1672－6553－2014－056

2014－05－16 收到第 1 稿，2014－06－21 收到修改稿．

*上海市青年科技启明星项目资助(14QB1402400)

E－mail:miaoxiaoting1983@126．com