运动学矢量参数测量方法*

李威 院老虎M．D．GERAIMCHUKV．P．ZINCHENKO

(1．沈阳航空航天大学航空航天工程学部，沈阳 1 10136)(2．乌克兰国立技术大学基辅理工学院，基辅 0 3056)

运动学矢量参数测量方法*

李威1†院老虎1M．D．GERAIMCHUK2V．P．ZINCHENKO2

(1．沈阳航空航天大学航空航天工程学部，沈阳 1 10136)(2．乌克兰国立技术大学基辅理工学院，基辅 0 3056)

研究了用于测量运动学矢量参数的测量方法．建立矢量测量装置的广义运动学模型及带有补偿的数学模型，得到敏感器运动分离后的简化模型．然后，通过具有电磁和静电支撑补偿的天平描述敏感器的运动，建立了作用在敏感器上的广义电磁力系统运动学方程．分析结果表明使用补偿模型可以建立新型模块化矢量测量装置，解决了分析侧向连接的影响．

矢量测量装置， 信息技术， 运动学， 数学模型

引言

随着信息技术、制造技术的发展对矢量测量装置(天平)提出了新的要求．虽然国内外很多学者对此进行了大量的研究，但是世界工业领域还没有模块化的矢量测量装置［1－2］．

矢量测量装置的发展趋势是建立集成测量单元，但是测量数据处理算法复杂，单独敏感器计量特性不同导致的测量误差，以及壳体变形和外部参数变化(温度，扰动，压力，等)［3］．大多数的矢量测试装置属于三分量矢量测量装置．随着iMEMS集成微电机系统发展，可以在iMEMS技术基础上生产测量装置，用于压力，力，速度，加速度等运动学参数测量或者同时抑制，特别是涉及到直接转换算法测量力学量算法复杂．

目前对于多分量矢量测量天平的原理、系统测量方法和模拟仿真的相关文章很少，限制了这一领域的发展．例如，伊布拉基莫夫［4］发表了基于单组元加速度计的矢量测量原理．众所周知的多组元测力和力矩的天平是接触式的，以平台形式完成，有6个自由度带有应力和应变传感器［5］．

随着信息技术的发展对构建天平这种复杂系统时提出更高的要求，建立统一的技术布局方案［6］，从而得到所有组元的完整信息(如，三个线速度和三个角度的测量信息)矢量校准信息．本文对不同类型的天平进行模拟仿真和综合分析，解决运动学矢量参数的测量方法．

1 矢量测量天平分类

矢量测量装置按原理分类:按测量参数的类型－速度、加速度、力、引力等;按测量坐标的数量，从单自由度到6自由度;电路结构－零平衡(带有反馈，闭环)和直接转换(开环)，零平衡天平取决于反馈回路的类型和使用的调节器，带有模拟继电控制和带有计算机/微处理器控制;按矢量测量装置上带有的传感元件类型－分为接触式和非接触式，非接触式分为电磁、电磁超导/低温和静电悬浮;按敏感器－带有光电、电磁和电容指示器的测量装置;调节器类型－带有通用调节器和随机调节器．

2 矢量测量装置的广义运动学模型

矢量测量装置广义数学模型建立在拉格朗日函数，广义动力学原理和达朗贝尔原理基础上，以下几个方面是广义运动学模型的基础［7］:

设计矢量测量装置的局部结构的力学参数，建立数学模型．

分析矢量测试装置动力学，信号处理算法分析和敏感元件控制系统(补偿网络);

3 直接转换天平广义运动学模型

天平广义运动学模型可以把敏感元件(绝对刚体)看作质量块和空间分布的弹性和阻尼元件的空间分布(如图1)，这样可以将它分为三个相关联的平动和三个角度位移．

图1 天平的广义示意图Fig．1 The generalized circuit of the vectorial converters

因此，坐标系原点位于敏感器质心位置O1;OX，OY，OZ坐标轴与主扭矩中心重合;弹性元件放置在XOY，XOZ，YOZ平面内;O1xyz是动框架与敏感器固联，O1位于它的质心;固定框架O1xy与天平相连;О1x，О1y，О1z的轴是敏感器的惯性轴;坐标系О1xyz和О1x'y'z'的坐标轴在初始时刻重合．

首先，直接转换的天平广义数学模型最终形式，认为敏感器是在惯性空间内以刚体形式运动，

得到系统方程如公式1所示:

这里Hn，Mn－重力场中的力和力矩;Hc和Mc－是弹性力的力和力矩;H(t)和M(t)是外力的力和力矩与时间的函数;

4 闭环天平广义运动学模型

考虑到，敏感器驱动在天平补偿中的影响不大，近似线性，此外不考虑在公式(1)中的角度转换．

因此(1)运动方程线性化合并组元，得到线性方程(2)中，对于固定结构的天平在这些合并组元接地时可以确定它的运动学模型:

这里Hk，Mk为相应的补偿力和力矩．

5 力学量测量的矢量测量装置运动学模型

研究带有挠性支撑，电磁，电磁超导和静电支撑的天平，分析每一种支撑的特性和在数学模型中的共性．

图2 矢量测量装置的改进示意图Fig．2 The improved circuit of the vectorial converters

弹性支撑天平的数学模型．定义，分别是弹性元件沿着О1z;О1y;О1z;轴的线刚度，分别是弹性元件绕着α，β，γ三个轴转动的旋转刚度(见图2)．考虑到Jx=Jy=Jz=J设计敏感元件时按照拉格朗日2型函数方程，系统在力场中按照刚体运动准线性化:

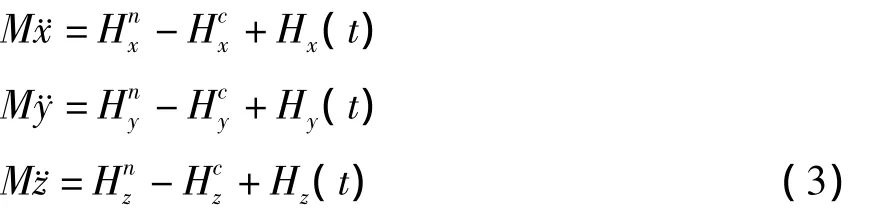
系统方程(3)描述带有弹簧支撑/没有补偿的敏感器运动．这种方式天平需要大量的转换和坐标变化，这样不能完成精确的线性化，并且(3)不能够用于分析侧向连接影响和选择元件，因为复杂连接在角度转换中被观测的组元有干扰存在．由于数学模型(3)的复杂性不可能从每一个组元上得到信息，所以在轴向带有弹性元件的布局的天平结构不能工程实现．

该解决方案区别于图1中的布局在于，弹性元件分布在与坐标轴平行的平面内并与坐标轴垂直，绕坐标轴旋转角度对弹性元件的载荷足够小．

在这种情况下，弹性元件沿着X轴的张力比Y轴上的张力大;增大X轴的张力2倍上面的元件受压缩(张力减小)，而第二个拉伸(张力增大);对于其它坐标方向弹性元件的变形都向一个方向．所以天平结构必须使用其它的布局，把载荷分解到各个坐标轴上，这对于减少组件干扰非常重要，包括在每一个接口使用信号处理算法．这种布局的解决方案实现如图2所示．

因此可以考虑前面的假设，简化矢量测量装置的数学模型，有6个弹性元件，和6个阻尼器［8］:

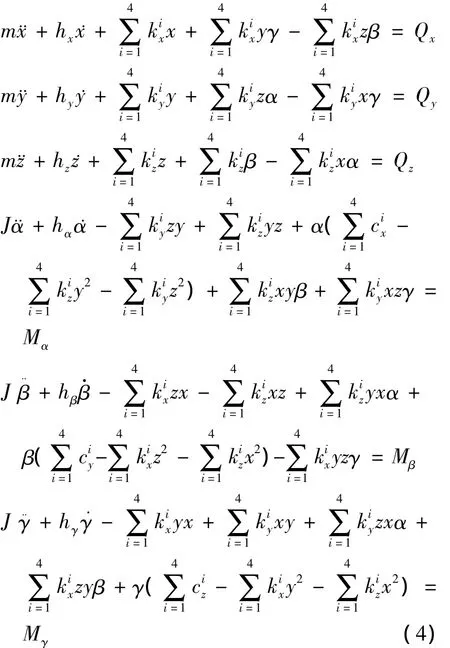
带入影响因素的伴随矩阵kij(i，j=)，则得到描述敏感器运动分离状态下的系统微分方程:

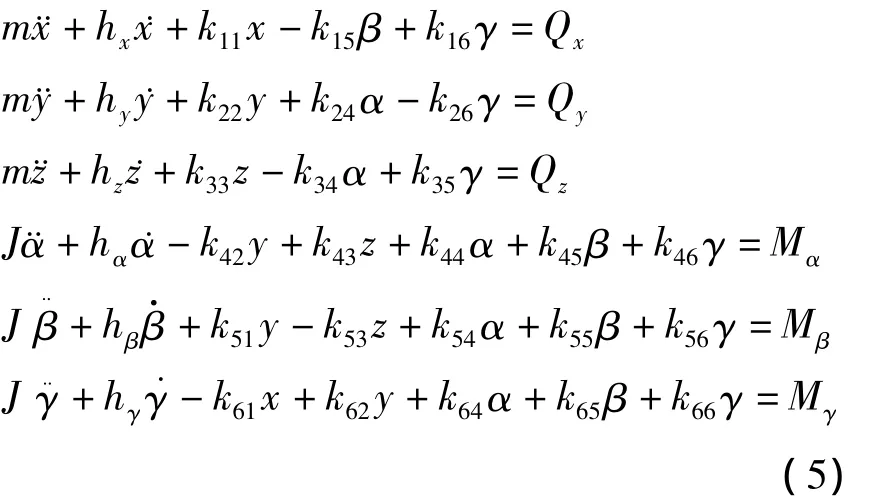
影响因素矩阵kij(i，j=1．6)为:

6 带电磁和静电支撑的测试装置运动学模型

带有弹性支撑的矢量测量装置限制了精度和灵敏度，可以用于测量量值大的参数，比如加速度从1g到5g．为了建立更高敏感度的矢量测量装置使用电磁/磁和静电悬浮形式．

为了确定数学模型采用拉格朗日－麦柯斯韦方程，描述敏感器运动，组元加入广义电磁力作用在敏感器上建立系统方程，描述装置电磁部分的作用过程．用类似的电磁力替换机械弹性元件，电磁天平和矢量变换带入(5)相应项中，得到下列系统方程:

这里:Io～=［i1+i2－(i3+i4)］，Io'=［i5+i6－(i7+i8)］，Iz=［i9+i10－ (i11+i12)］，Iα=(i1－i2+i3－i4)，Iβ=(i5－i6+i7－i8)，Iγ=(i9－i10+i11－i12)，ii线圈里的控制电流i=1，2，…，12;I－敏感器的操纵和控制算法．

在完全使用电磁悬浮结构时(敏感器和天平之间没有机械连接)，在系统方程(6)必须去除机械弹性和阻尼元件组元．矢量测量装置带有运动线圈，线圈的导向器影响其精度．

设计带有电磁支撑矢量测试装置的补偿器，实际是设计带有超导电磁支撑的矢量测试装置．超导支撑设计可以利用磁力势效应(VV Kozorezom发现的)完成，在两个电磁元件间或者理想情况下的主环之间存在最小电势能．由于没有张弛运动和温度噪声的影响，利用超导性可以显著提升测量值的精度．这种矢量测量装置由超导电磁电路组成，电路对敏感器产生对称的力．这种矢量测量装置，在理想电流情况下，整个电磁场不变，在物理上保证了敏感器的支撑稳定性．利用超导电磁支撑的原理工作，功率损失为零，具有高稳定性和可靠性．

构建这种矢量测量装置可以利用高敏感度的重力测量装置和梯度测量仪，利用电磁场势能效应．这样的矢量测量装置没有反馈控制网络．系统微分方程，描述超导电磁敏感器运动，与系统方程(6)相符，具体如下:

这里Xi={x，y，z，α，β，γ};，复合函数包括独立的导数和积分函数．

必须指出，在设计矢量测量装置的补偿电路时，系统方程(7)必须加入扰动检测方程．除了完成微分方程(6)和(7)中变量替换类似求解空间变量方程［9］．对于分析采用静电支撑的天平敏感器运动，可以利用系统方程(7)，只需用静电支撑项替换电磁天平项即可．需要指出，使用静电支撑天平有局限性，首先静电支撑工作必须采用很高的电压，其次敏感器必须与导向器联合使用，导向器的存在影响敏感器并降低精度和灵敏度．换言之，导向器完全破坏了静电支撑的优势．

7 结论

电磁和静电支撑补偿的运动学模型，能够用于描述敏感器的控制、过程分析和建立信号处理算法．研究表明按照通常的布局设计天平无法计算一个轴对另一个轴的影响，而通过补偿设计结构解决了这一限制，能够解决运动学矢量参数的测量方法．

1 Herayimchuk M D．Status and development of measurement tools vector mechanical values．Ukrainian Scientific－Technical Journal Vibrate in Technics and Technologies，2003，4(30):38～39

2 Herayimchuk M D，Ivanov J E．The study of multi－transducers of mechanical quantities．Kiev Vipol，1996，2:108 ～110

3 Schwab L，Seleznev A．Measurement of angular accelerations．Mechanical Engineering，1983，5:160 ～163

4 Ibragimov I H．Theoretical Foundations of measuring the characteristics of acceleration field．Mechanical Engineering，1979:167～169

5 Zinchenko V P．Methodology for the design of primary sources．Scientific News KPI，2001，5:69 ～82

6 Zinchenko V P，Zinchenko N P．The design procedure vnutrimodelnyh tenzovahiv．Journal of NTU KPI:Mashinostroenie，1999，34:319 ～328

7 Vinogradov I M．Mathematical encyclopedia．Soviet Encyclopedia，1976，5:24 ～27

8 Geraimtchouk M D，Geraimtchouk I M．Design methods and modeling of multi(six)－coordinates acceleration sensors for navigation systems．Technical Journal Control of Industrial Systems，1997，2:75 ～76

9 Heraymchuk M D．process control system in real time．Technical Electrodynamics，2003，3:92～93

10 Zinchenko V P，Zinchenko N P．Designing a component of information technology of strain－gauge experimental researches．Proceedings of NAU，2005，2(24):21 ～24

11 Zinchenko V P．The method of mathematical modeling of mechanical aerodynamic balance．Mechanical Engineering，2001，41:79 ～86

12 Zinchenko V P．Methodology designing sources of information．Scientific lead KPI，2001，5:69～82

*The project supported by the Natural Science Foundation jointly funded of Liaoning Province(2013024005)and Based Research Projects funded of Shenyang(F13316158)

† Corresponding author E－mail:252133160@qq．com

THE MEASURING METHOD OF KINEMATIC VECTOR PARAMETE*

Li Wei1†Yuan Laohu1M．D．GERAIMCHUK2V．P．ZINCHENKO2
(1．Faculty of Aerospace Engineering of Shenyang aerospace university，Shenyang110136，China)(2．National Technical University of Ukraine Kiev Polytechnic institute，Kiev03056，Ukraine)

The measuring method used to measure kinematic vector parameters was researched．The generalized kinematics model of vector measuring device and a mathematical model with compensation were established，consequently，the simplified model of the separated sensor movement was obtained．Afterwards，based on the sensor movement described by the balance of electromagnetic and electrostatic support and compensation，the kinematics equations of generalized electromagnetic force system for the sensor were derived．Analysis results show that the use of the compensation model can establish a new modular vector measuring device，thus，the influence owing to the analysis of lateral connections is solved．

vector measuring device， information technologies， kinematic， mathematical model

1 July 2014，

14 July 2014．

10．6052/1672－6553－2014－055

2014－07－01 收到第 1 稿，2014－07－14 收到修改稿．

*辽宁省自然基金联合基金(2013024005)和沈阳市基础科研基金资助(F13316158)

E－mail:252133160@qq．com